Записать уравнения которым удовлетворяют электромагнитные потенциалы

Электродинамические потенциалы. Общий случай

Выведенные в предыдущем разделе дифференциальные уравнения позволяют в принципе определить векторы Е и Н через функции jст и ρст. Однако наличие в их правых частях выражений grad ρст и rot jст в ряде случаев несколько затрудняет получение удобных расчетных формул. Поэтому указанные уравнения обы­чно используют в тех случаях, когда сторонние источники рас­положены за пределами рассматриваемой области, т.е. когда уравнения (2.27) и (2.28) становятся однородными и соответ­ственно уравнения (2.31) и (2.32) переходят в (2.33) и (2.34).

В общем случае для определения векторов поля по заданным источникам обычно применяют искусственный прием: сначала находят вспомогательные функции, а потом через них вычисляют векторы Е и Н. Эти вспомогательные функции можно ввести различным образом в зависимости от специфических особенно­стей анализируемой задачи. Для упрощения решения многих задач вводят так называемые электродинамические потенциалы. Рассмотрим систему уравнений Максвелла (2.25). Последнее уравнение этой системы представляет собой четвертое уравнение Максвелла div В = 0, записанное для случая однородной изо­тропной среды. Так как дивергенция ротора любого вектора равна нулю (div rot a = 0), то из уравнения div В = 0 следует, что вектор В можно представить в виде В = rot А. При этом вектор

(2.35)

При известном векторе А уравнение (2.35) позволяет одно­значно найти вектор Н. Однако оно допускает некоторый произвол в определении вектора А. Действительно, если вместо А взять вектор A1 = А + grad ψ, где ψ– произвольная скалярная функция, то значение вектора Н не изменится, так как

rot grad ψ = 0. (2.36)

Неоднозначность определения вектора А будет использована при выводе дифференциального уравнения для А.

Подставим выражение (2.35) во второе уравнение системы (2.25) и изменим порядок дифференцирования по времени и пространственным координатам. Объединив затем векторы Е и под знаком ротора, получим rot(E +) = 0. Учитывая тождество (2.36), можно положить, что стоящее под знаком ротора выражение равно – grad и, где u – некоторая скалярная функ­ция, или

(2.37)

Знак минус перед grad и в формуле (2.37) введен, чтобы в случае электростатического поля функция uсовпадала с обычным эле­ктростатическим потенциалом.

Таким образом, все векторы, определяющие электромаг­нитное поле, выражаются через две функции: векторный поте­нциал А и скалярный потенциал и. Следовательно, задача состоит теперь в том, чтобы найти функции А и и. Подставляя (2.35) и (2.37) в первое уравнение системы (2.25) и преобразовывая левую часть получающегося при этом соотношения с помощью тождества (2.26), приходим к равенству

(2.38)

Упростим уравнение (2.38). Как уже отмечалось, вектор А определен с точностью до градиента произвольной скалярной функции. Следовательно, можно потребовать, чтобы вектор А удовлетворял добавочному условию. Потребуем, чтобы

(2.39)

Соотношение (2.39) принято называть условием калибровки. С учетом (2.39) уравнение (2.38) принимает вид

(2.40)

Аналогичное уравнение получается и для скалярного потен­циала и. Подставляя (2.37) в третье уравнение системы (2.25), получаем

Используя условие калибровки (2.39) и тождество div grad и = = 2u, приходим к уравнению

(2.41)

Таким образом, векторный и скалярный потенциалы, как и векторы Е и Н, удовлетворяют неоднородным уравнениям Даламбера. Однако правые части уравнений для потенциалов имеют более простой вид. Поэтому уравнения (2.40) и (2.41) оказываются более удобными при решении многих конкретных задач.

Найдем частные решения уравнений (2.40) и (2.41), считая функции jст и ρст известными. Вначале рассмотрим уравнение (2.41). Предположим, что электрическое поле создается точечным неподвижным зарядом постоянной величины Q = const, располо­женным в начале координат, вектор Е в этом случае определяется выражением (1.7). Так как поле не должно зависеть от времени, то =0 и соотношение (2.37) принимает вид E= -grad u. Рас­писывая grad и в сферической системе координат r, θ, φ, (см. приложение 4) и учитывая, что вектор Е в рассматриваемом случае может зависеть только от координаты r(от расстояния от заряда Q до точки наблюдения), получаем

(2.42)

где r0 – координатный орт переменной r. Подставляя выражение (2.42) в (1.7) и выполняя интегрирование по переменной r, находим функцию и:

Постоянная интегрирования в (2.43) принята равной нулю, чтобы при r→∞ функция и обращалась в нуль. Формула (2.43) полностью совпадает с известным из курса общей физики вы­ражением для электростатического потенциала точечного заряда (см. замечание по поводу выбора знака перед grad и в выражении (2.37)). Если заряд сосредоточен в малом элементе объема dVс плотностью ρст, то и = ρстdV/(4πεR), где R– расстояние от элемента dVдо точки наблюдения. От этой формулы легко перейти к выражению для электростатического потенциала, создаваемого произвольным распределением зарядов в объеме V. В соот­ветствии с принципом суперпозиции получаем

(2.44)

Значение и,определяемое формулой (2.44), можно рассма­тривать как решение уравнения

, (2.45)

получающегося из равенства (2.41), если в последнем положить . Уравнение (2.45) называют уравнением Пуассона.

Если в рассматриваемой части пространства заряды отсутствуют(ρст = 0), то(2.45) переходит в уравнение Лапласа: .

Предположим теперь, что поле также соз­дается точечным зарядом, расположенным в начале координат, но величина этого заряда изменяется со временем Q = Q(t).Тогда в любой точке, кроме начала координат, потен­циал и будет удовлетворять однородному урав­нению Даламбера

(2.46)

Для решения уравнения (2.46) удобно использовать сфери­ческую систему координат r, θ, φ (рис. 2.5). Оператор Лапласа в этой системе координат определяется формулой (П. 18). Так как поле создается точечным зарядом, расположенным в начале координат, то потенциал и не должен зависеть от углов θ и φ. Поэтому уравнение (2.45) можно переписать в виде:

Рис. 2.5. Сферическая система координат

Учитывая, что и переходя от u к функции u1, связанной с uсоотношением u1 = ru, получаем:

(2.47)

Общее решение уравнения (2.47) имеет вид u1 = f1(t-r/c)+f2(t+r/c), где f1(t-r/c) и f2(t+r/c) – произвольные дважды диф­ференцируемые функции аргументов t-r/c и t+r/cсоответ­ственно. В том, что функции f1(t-r/c) и f2(t+r/c)удовлетворяют (2.47), можно убедиться непосредственной подстановкой их вэто уравнение. Таким образом, скалярный потенциал и можно пред­ставить в виде

(2.48)

Первое слагаемое в выражении (2.48) представляет собой волну, распространяющуюся из начала координат вдоль ради­усов rсоскоростью света . Действительно, функция f1(t-r/c) в фиксированный момент времени tимеет одинаковые значения на сфере радиуса r = const. В момент времени t+Δt функция f1(t-r/c) принимает то же значение на сфере радиуса r+cΔt, так как

t+ Δt – (r+cΔt)/c = t– r/с. Волны типа (1/r) f (t-r/c)принято называть расходящимися сферическими волнами. Соот­ветственно второе слагаемое в выражении (2.48) представляет собой сферическую волну, распространяющуюся из бесконечности со скоростью света с и сходящуюся к началу координат. Отметим существенную особенность функций, описывающих волновые про­цессы. Они всегда содержат множители вида f(t± r/ v), характер зависимости которых от расстояния вдоль направления распро­странения волны в фиксированный момент времени повторяет характер их зависимости от времени в фиксированной точке пространства, a v – скорость распространения волны.

Если источники поля сосредоточены в ограниченной области, то сходящаяся сферическая волна может возникнуть только в результате отражения расходящейся сферической волны. Так как пространство считается однородным, то отраженной волны не может быть, и функцию f2(t+r/c)нужно считать равной нулю. Следовательно, u = f1(t-r/c)/r.Значения потенциала и должны быть связаны с интенсивностью источников поля. В рассмат­риваемом случае источником поля является точечный заряд Q(t). Полученное выражение для и должно быть справедливым при любом законе изменения функции Q(t).Так как в статическом случае потенциал и определяется формулой (2.43), естественно предположить, что f1(t-r/c)=Q(t-r/c)/(4πε). Тогда u=Q(t-R/c)/(4πεr). Если заряд сосредоточен в малом элементе объема dVс пло­тностью ρст = ρст (t), то скалярный потенциал u=ρст(t-R/c)dV/(4πεR), где R – как и ранее, расстояние от элемента dVдо точки наблю­дения. От этой формулы легко перейти к выражению для скалярного потенциала, обусловленного произвольным распреде­лением сторонних зарядов в объеме V:

(2.49)

ξ, η, ζ – декартовы координаты элемента dV; x, у, z -декартовы координаты точки наблюдения N; элемент объема dV= dξdηdζ(рис. 2.6).

Рис. 2.6. Элемент dV и точка наблюдения N

Выражение (2.49) является частным решением неоднородного уравнения Даламбера (2.41).

Аналогично можно записать и решение уравнения (2.40). Для этого нужно в (2.49) заменить uна А, ρст на jст и ε на 1/μ. В результате получим:

(2.50)

Из (2.49) и (2.50) следует, что для вычисления электродинамических потенциалов u и А в произвольной точке прост­ранства N = N(x, у, z)вмомент времени tнужно брать значения токов и зарядов в каждом элементе dV вболее ранний по срав­нению с tмомент времени t¢ = t–R/c, определяемый расстоянием Rот элемента dVдо точки наблюдения N(х, у, z) (рис. 2.6). Иными словами, влияние источников электромагнитного поля проявляется не мгновенно: требуется некоторое время Δt = R/c, за которое электромагнитные колебания, вызванные зарядами и токами в элементе dV, успеют распространиться от элемента dVдо точки наблюдения. Поэтому функции А и u в форме (2.50) и (2.49) часто называют запаздывающими потенциалами.

Тема 11. Электродинамические потенциалы. Основные теоремы и принципы электродинамики

Постановка задач в электродинамике. Скалярный и векторный электродинамические потенциалы. Уравнения Даламбера для электродинамических потенциалов. Уравнения Пуассона и Лапласа. Связь электродинамических потенциалов с векторами ЭМП. Решение неоднородных уравнений Даламбера для электродинамических потенциалов. Запаздывающие потенциалы.

Применение электродинамических потенциалов в анализе ЭМП.

Основные теоремы и принципы в теории гармонических полей. Магнитные токи и заряды. Принцип перестановочной двойственности уравнений Максвелла. Теорема единственности для внешней и внутренней задач электродинамики. Принцип эквивалентности. Различные формулировки принципа эквивалентности. Лемма Лоренца. Сопряженная лемма. Теорема взаимности.

Указания к теме

Необходимо выучить определения скалярного и векторного потенциалов, обратить внимание на их связь с векторами и энергией ЭМП, а также на применение в анализе ЭМП; уяснить понятие запаздывающего потенциала.

Пользуясь теоремой Пойнтинга о балансе энергии, можно определить дополнительные условия, наложение которых сообщает решениям уравнений Максвелла физическую определенность (единственность).

Следует выучить формулировки теорем единственности и взаимности, принципов эквивалентности и двойственности, обратить внимание на их место в теории ЭМП.

Основные сведения

При решении задач излучения необходимо решать систему уравнений Максвелла при наличии сторонних источников ЭМП. Введение электродинамических потенциалов позволяет упростить расчет ЭМП излучающих систем. Из условия соленоидальности магнитного поля (2.8) можно записать:

Þ , (11.1)

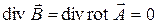
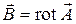
где введенную функцию называют векторным потенциалом.

Подстановка выражения (11.1) в (2.6) позволяет связать с :

или . (11.2)

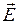
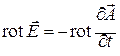
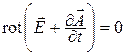
Из условия потенциальности электростатического поля

Þ , (11.3)

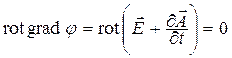
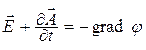
где введенную функцию j называют скалярным потенциалом (в случае электростатического поля функция jявляется скалярным электрическим потенциалом)[1, 11].

Векторы ЭМП можно выразить через и j :

, . (11.4)

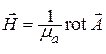
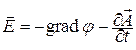
Волновые уравнения для электродинамических потенциалов.Подставляя выражение (11.4) в систему уравнений Максвелла для однородной среды при наличии сторонних источников ЭМП, получаем

. (11.5)

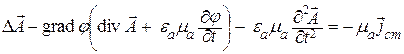
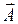
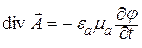
Удобно выбрать div так, чтобы в уравнении (11.5) слагаемое в скобках оказалось бы равным нулю

. (11.6)

Условие (11.6) называют калибровкой Лоренца. В случае равенства нулю правой части (11.6) получается калибровка Кулона [1–3, 11].

С учетом выражения (11.6) из системы уравнений Максвелла получаются неоднородные волновые уравнения для потенциалов и j

; (11.7)

. (11.8)

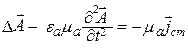
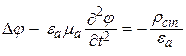
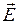
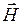
После решения уравнений (11.7) и (11.8) для конкретных исходных данных векторы и находятся после подстановки и j в (11.4).

В случае стационарного магнитного поля можно считать потенциальной энергией токов, в то же время j связан с потенциальной энергией зарядов в электростатике [1–3].

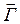
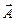
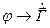
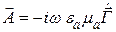
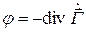
При решении задач излучения с целью уменьшения числа неизвестных иногда вводят вектор Герца [12] ( , ).

, . (11.9)

В классической электродинамике и j – лишь вспомогательные величины, так как для представления ЭМП необходим переход к и . В квантовой электродинамике и j считаются фундаментальными величинами [1–3].

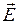
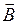
Электродинамические потенциалы в безграничном пространстве.Решение уравнений (11.7) и (11.8) в безграничном пространстве упрощается. В пространстве вне точечного источника r_ст = 0.

Для точечного заряда в ССК и ЦСК решение имеет вид [1–4]

. (11.10)

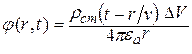
При v®¥ (мгновенное распространение действия ЭМП) из уравнений (11.8) получается уравнение С. Пуассона [1, 6, 11] : .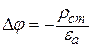

При точках незаряженной области (r = 0) уравнение Пуассона (11.15) переходит в уравнение П. Лапласа [6, 11] : .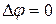

Волновое уравнение для векторного потенциала имеет вид [1–3, 11]

(11.11)

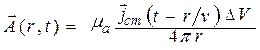
Полученные решения (11.10) и (11.11) отражают конечность скорости распространения ЭМП от своих источников. В точке наблюдения значения электродинамических потенциалов (а значит, и векторов ЭМП) определяются значением не в текущий момент времени t, а в предшествующий момент t – r/v. Поэтому решения (11.10) и (11.11) называют запаздывающими потенциалами. Время запаздывания r/v как раз показывает, какое время требуется ЭМВ, чтобы пройти расстояние r с конечной скоростью v [11].

Сравнивая уравнения (11.10) и (11.11) с (5.5) и (5.6), можно сделать вывод, что полученные решения имеют характер сферических волн.

При решении задач электродинамики выделяют внутреннюю и внешнюю задачи. Внутренней называется задача определения ЭМП внутри области V, ограниченной замкнутой поверхностью S (рис. 11.1), при заданных на ней граничных условиях для векторов ЭМП. Примеры внутренней задачи – определение ЭМП в объемном резонаторе, определение функции распределения тока в антенне заданной конструкции.

Внешняя задача электродинамики заключается в решении уравнений Максвелла для неограниченного пространства вне области V, ограниченной замкнутой поверхностью S , при наличии источников ЭМП. Примеры внешней задачи – определение ЭМП антенны в свободном пространстве при известном распределении тока в антенне, решение задач дифракции.

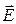
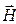
При постановке задач электродинамики необходимо ввести начальные и граничные условия, сообщающие этим задачам физическую определенность [1]. Векторы ЭМП не могут иметь произвольную зависимость от координат и времени. Например, есть ограничения на скорость убывания амплитуд и .

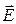
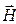
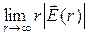
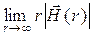
Из закона сохранения энергии следует [1], что в пространстве без потерь каждый из векторов и должен убывать не медленнее, чем 1/r . Это условие называется условием излучения на бесконечности [1]:

= 0 ; = 0 . (11.12)

Условия (11.12) эквивалентны условиям излучения Зоммерфельда

= 0 ; = 0 . (11.13)

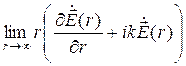
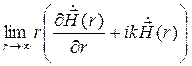
Знак при вторых слагаемых в уравнениях (11.13) определяет, что условия записаны для ЭМВ, которая расходится (удаляется) от источника [1, 5]. При наличии потерь в пространстве, которые учитываются коэффициентом затухания a, векторы ЭМП убывают быстрее – пропорционально exp(–ar)/r.

Существуют принципы и теоремы электродинамики, которые позволяют существенно упростить решение задач электродинамики и теории антенн.

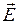
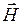
Теорема единственности решений уравнений Максвелла.Методы решения уравнений ЭМП могут быть различными, поэтому необходимо доказать, что решение, полученное любым методом, является единственным. В учебных пособиях [1, 12] приведено доказательство того, что если при решении уравнений Максвелла при определенных начальных и граничных условиях получены значения векторов ЭМП ( и ), то это решение будет единственным.

Принцип двойственности. Для решения задач теории ЭМП удобно ввести понятия магнитных токов и зарядов. Как отмечалось ранее, эти величины являются фиктивными и вводятся как эквивалент действия электрических токов.

При наличии магнитных источников уравнения Максвелла (2.20)–(2.21) уступают место следующим [1, 13]:

= = , , (11.14)

= = , . (11.15)

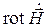
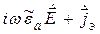
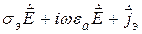
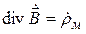
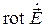
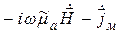
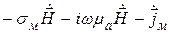
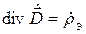
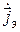
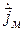
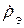
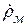
где и – плотности сторонних электрического и магнитного токов соответственно; s_м – удельная эквивалентная магнитная проводимость; и – объемные плотности электрического и магнитного зарядов.

Сопоставляя уравнения Максвелла и выражения (11.14)–(11.15), нетрудно убедиться, что одни полностью переходят в другие при следующей замене:

® , ® , ® , ® , ® , e_a « µ_a , s_э « s_м,

, ® – , ® – , ® – , ® – , ® – . (11.16)

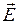
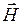
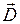
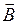
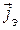
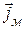
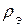
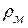
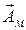
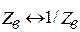
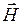
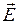
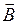
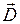
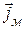
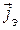
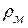
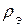
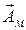
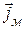
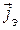
Следует отметить, что размерности эквивалентных величин несколько отличаются от обычных в системе СИ. Оказывается, что измеряется в вольтах на метр квадратный, а не в амперах на метр квадратный, как , I_м – в вольтах (размерность U), Q_м – в веберах (размерность Ф), s_м – в омах на метр (размерность удельного сопротивления) [1, 7], то есть размерности прямой и обратной замены отличаются как сопротивление и проводимость!

Таким образом, если найдено ЭМП заданных электрических источников, то достаточно сделать замену (11.16) в готовом решении задачи, и это непосредственно приведет к выражению ЭМП излучения магнитных источников.

Общий смысл принципа двойственности состоит в том, что при определенных условиях электрическое и магнитное поля «меняются ролями». Кроме того, симметрия системы уравнений Максвелла (11.14)–(15.9) подчеркивает равноправие электрических и магнитных составляющих в переменном ЭМП.

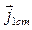
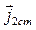
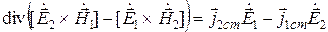
Лемма Лоренца. Пусть в некоторой линейной среде имеется два электрических источника, характеризуемых функциями плотности стороннего электрического тока и соответственно (рис. 11.2). После преобразований

. (11.17)

Интегрируя уравнение (11.17) по области V, ограниченной поверхностью S, охватывающей источники ЭМП, с учетом теоремы Остроградского – Гаусса (2.11) получим

. (11.18)

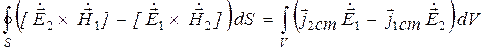
Соотношения (11.17) и (11.18) – это соответственно дифференциальная и интегральная формулировки леммы Лоренца, устанавливающей важные связи между полями двух источников.

В случае свободного пространства в дальней зоне источников (S®∞) левая часть соотношения (11.18) стремится к нулю [1, 5, 6], а это приводит к таким соотношениям:

, . (11.19)

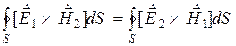
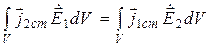
Принцип взаимности разделенных источников. В случае, когда источники разделены в пространстве, первый источник расположен в области V₁, а второй – в области V₂ (рис. 11.2), соотношения (11.19) принимают форму

. (11.20)

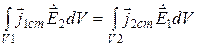
Интеграл справа можно истолковать как некоторую характеристику взаимодействия ЭМП первого источника с ЭМП второго; аналогичный смысл имеет интеграл слева. Очевидно, что характеристики такого рода равны независимо от типа источников и изотропных сред, в которых они расположены.

Соотношение (11.20) выражает принцип взаимности, подразумевая пространственно разделенные источники и их поля.

Для двух линейных токов из выражения (11.20) следует [1]

, (11.21)

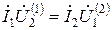
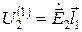
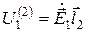
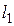
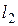
где и представляют собой э. д. с., наводимые на каждом из линейных элементов (I1) и (I2) полем другого источника.

Равенство (11.21) можно представить в другой форме:

Þ , (11.22)

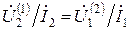
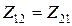
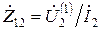
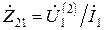
где и имеют смысл взаимных сопротивлений.

Принцип взаимности проявляется в том, что э. д. с., наводимая на первом элементе заданным током второго, оказывается такой же, как и э. д. с. на втором элементе при равном токе первого [1].

Э. д. с., наводимая в приемной антенне в зависимости от ее ориентации, изменяется по тому же закону, что и ЭМП в дальней зоне, создаваемое этой антенной в режиме передачи. То есть направленность действия антенны при приеме и передаче одинакова. В теории антенн принцип взаимности позволяет использовать характеристику направленности передающей антенны (ДН) при использовании этой антенны в качестве приемной, а также использовать измеренную характеристику ДН приемной антенны и в режиме передачи.

Среды, устройства и системы, в которых выполняется принцип взаимности, называют взаимными [1].

Список рекомендуемой литературы:[1, гл. 11, 15, с. 55–59, 83–90; 2, с. 75–78, 123–126, 132–139, 150–152; 3, гл. 11, с. 51–55; 4, с. 47–50; 5, с. 21–24, 52–55, 223–239; 6, с. 128–138, 172, 205–212; 7, с. 63–67, 244–279; 8, с. 18–25, 57–61; 9, с. 60–61, 143–154, 157–159; 10, с. 68–70; 11, с. 61–75, 121–125; 12, с. 63–65, 94–98, 106–132; 13, с. 134–140, 150–155, 165–168, 238–241; 32, с. 13–17; 34, с. 5–10; 35, с. 11–13; 36, с. 9–12].

Контрольные вопросы и задания

1. Дайте определение электродинамическим потенциалам ЭМП.

2. Что дает введение электродинамических потенциалов?

3. Почему потенциалы называют «запаздывающими»?

4. Существует ли связь электродинамических потенциалов с энергией ЭМП?

5. С помощью какого из электродинамических потенциалов можно охарактеризовать потенциальную энергию зарядов в электростатическом поле?

6. Какой потенциал связан с потенциальной энергией токов в случае стационарного магнитного поля?

7. Каково место электродинамических потенциалов в теории ЭМП и теории антенн?

8. Укажите условия калибровки волновых уравнений для электродинамических потенциалов. Зачем нужны условия калибровки?

9. Можно ли скалярный потенциал назвать «электростатическим»?

10. Существуют ли магнитные токи и заряды?

11. Дайте определение внешней и внутренней задач электродинамики.

12. В чем смысл принципа двойственности?

13. Назовите формулировку теоремы единственности. Какие требования предъявляются к функциям, описывающим ЭМП для выполнения теоремы единственности?

14. Дайте формулировку принципа эквивалентности.

15. В чем заключается смысл теоремы взаимности?

Решение уравнений Максвелла; потенциалы и волновое уравнение

Теперь стоило бы заняться немного математикой; мы запишем уравнения Максвелла в более простой форме. Вы, пожалуй, сочтете, что мы усложняем их, но если вы наберетесь терпения, то внезапно обнаружите их большую простоту. Хотя вы уже вполне привыкли к каждому из уравнений Максвелла, имеется все же много частей, которые стоит соединить воедино. Вот как раз этим мы и займемся.

Начнем с V·В=0 — простейшего из уравнений. Мы знаем, что оно подразумевает, что В — есть ротор чего-то. Поэтому, если вы записали

то считайте, что уже решили одно из уравнений Максвелла. (Между прочим, заметьте, что оно остается верно для другого вектора А′, если A′=A+ vψ), где ψ — любое скалярное поле, потому что ротор vψ — нуль и В — по-прежнему то же самое. Мы говорили об этом раньше.)

Теперь разберем закон Фарадея VxE= –∂B/∂t, потому что он не содержит никаких токов или зарядов. Если мы запишем В как V X А и продифференцируем по t, то сможем переписать закон Фарадея в форме

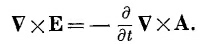Поскольку мы можем дифференцировать сначала либо по времени, либо по координатам, то можно написать это уравнение также в виде

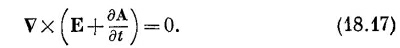Мы видим, что E+∂A/∂t — это вектор, ротор которого ранен нулю. Поэтому такой вектор есть градиент чего-то. Когда мы занимались электростатикой, у нас было VxE=0, и мы тогда решили, что Е — само градиент чего-то. Пусть это градиент от –φ (минус для технических удобств). То же самое сделаем и для E+∂A/∂t; мы полагаем

Мы используем то же обозначение φ, так что в электростатическом случае, когда ничто не меняется со временем и ∂A/∂t исчезает, Е будет нашим старым –vφ. Итак, закон Фарадея можно представить в форме

Мы уже решили два из уравнений Максвелла и нашли, что для описания электромагнитных полей Е и В нужны четыре потенциальные функции: скалярный потенциал φ и векторный потенциал А, который, разумеется, представляет три функции.

Итак, А определяет часть Е, так же как и В. Что же произойдет, когда мы заменим А на A′=A+vψ? В общем, Е должно было бы измениться, если не принять особых мер. Мы можем, однако, допустить, что А изменяется так, чтобы не влиять на поля Е и В (т. е. не меняя физики), если будем всегда изменять А и φ вместе по правилам

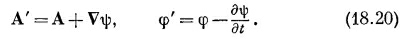Тогда ни В, ни Е, полученные из уравнения (18.19), не меняются.

Раньше мы выбирали V ·А=0, чтобы как-то упростить уравнения статики. Теперь мы не собираемся так поступать; мы хотим сделать другой выбор. Но подождите немного, прежде чем мы скажем, какой это выбор, потому что позднее станет ясно, почему вообще делается выбор.

Сейчас мы вернемся к двум оставшимся уравнениям Максвелла, которые свяжут потенциалы и источники ρ и j. Раз мы можем определить А и φ из токов и зарядов, то можно всегда получить Е и В из уравнений (18.16) и (18.19) и мы будем иметь другую форму уравнений Максвелла.

Начнем с подстановки уравнения (18.19) в v·E=ρ/ε₀; получаем

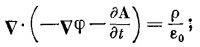это можно записать еще в виде

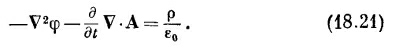Таково первое уравнение, связывающее φ и А с источниками.

Наше последнее уравнение будет самым трудным. Мы начнем с того, что перепишем четвертое уравнение Максвелла:

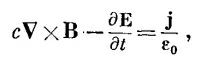а затем выразим В и Е через потенциалы, используя уравнения (18.16) и (18.19):

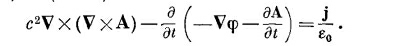Первый член можно переписать, используя алгебраическое тождество v x (vxA) = V (V·A) – v 2 A; мы получаем

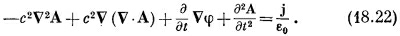Не очень-то оно простое!

К счастью, теперь мы можем использовать нашу свободу в произвольном выборе дивергенции А. Сейчас мы собираемся сделать такой выбор, чтобы уравнения для А и для φ разделились, но имели одну и ту же форму. Мы можем сделать это, выбирая ,

Когда мы поступаем так, то второе и третье слагаемые в уравнении (18.22) погашаются, и оно становится много проще:

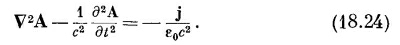И наше уравнение (18.21) для φ принимает такую же форму:

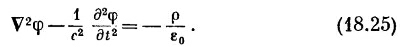Какие красивые уравнения! Они великолепны прежде всего потому, что хорошо разделились — с плотностью заряда стоит φ, а с током стоит А. Далее, хотя левая сторона выглядит немного нелепо — лапласиан вместе с (∂/∂t) 2 , когда мы раскроем ее, то обнаружим

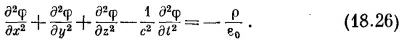Это уравнение имеет приятную симметрию по х, у, z, t; здесь (–1/с 2 ) нужно, конечно, потому, что время и координаты различаются; у них разные единицы.

Уравнения Максвелла привели нас к нового типа уравнению для потенциалов φ и А, но с одной и той же математической формой для всех четырех функций φ, А_х, А_у и A_z. Раз мы научились решать эти уравнения, то можем получить В и Е из vXE и —vφ —∂A/∂t. Мы приходим к другой форме электромагнитных законов, в точности эквивалентной уравнениям Максвелла; с ними во многих случаях обращаться гораздо проще.
Фактически мы уже решали уравнение, весьма похожее на (18.26). Когда мы изучали звук в гл. 47 (вып. 4), мы имели уравнение в форме

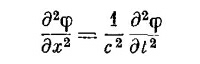и видели, что оно описывает распространение волн в x-направлении со скоростью с. Уравнение (18.26) это соответствующее волновое уравнение для трех измерений. Поэтому в области, где больше нет зарядов и токов, решение этих уравнений не означает, что φ и А — нули. (Хотя на самом деле нулевое решение есть одно из возможных решений.) Имеются решения, представляющие некоторую совокупность φ и А, которые меняются со временем, но всегда движутся со скоростью с. Поля передвигаются вперед через свободное пространство, как в нашем примере в начале главы.

С новым членом, добавленным Максвеллом в уравнение IV, мы смогли записать полевые уравнения в терминах А и φ в форме, которая проста и сразу же позволяет выявить существование электромагнитных волн. Для многих практических целей еще будет удобно использовать первоначальные уравнения в терминах E и В. Но они — по ту сторону горы, на которую мы уже вскарабкались. Теперь мы можем посмотреть вокруг. Все будет выглядеть иначе — нас ожидают новые, прекрасные пейзажи.