Записать уравнения ребер призмы oabo1a1b1

Экзаменационные задачи по ЛА

ВЫСШАЯ МАТЕМАТИКА

ИЭТ, Эл-12,13,14,16,17,18, 1 семестр, 2017/2018 уч. год

Лекторы: доц. Янченко А.Я., ст. преп. Подкопаева В.А.

Экзаменационная программа

1. Производная. Определение, механический и геометрический смысл.

Уравнение касательной и нормали.

2. Производная. Определение. Таблица производных элементарных функций.

3. Дифференцируемость функции в точке. Критерий дифференцируемости.

4. Дифференцируемость функции в точке. Необходимое условие дифференци-руемости. Арифметические свойства дифференцируемых функций

5. Теорема о производной сложной функции.

6. Дифференциал функции и его основные свойства.

7. Локальные экстремумы функций. Необходимое условие экстремума дифферен-цируемой функции.

8. Свойства функций, непрерывных на отрезке. Теорема Ролля.

9. Теоремы Лагранжа и Коши.

10. Правило Лопиталя.

11. Условия монотонности дифференцируемой функции.

12. Достаточные условия локального экстремума.

13. Выпуклость. Достаточное условие выпуклости.

14. Точки перегиба. Необходимое условие перегиба. Достаточное условие перегиба

(по второй производной).

15. Формула Тейлора с остаточным членом в форме Лагранжа.

16. Формула Тейлора с остаточным членом в форме Пеано.

17. Асимптоты графика функции. Общая схема исследования функции и

18. Производная обратной функции. Производные

19. Производные функций, заданных параметрически.

20. Геометрические векторы.

21. Скалярное произведение векторов. Векторное произведение векторов. Смешанное произведение векторов.

22. Плоскость и прямая в пространстве. Основные задачи о прямых и плоскостях.

23. Определители n-го порядка. Вычисление и свойства.

24. Матрицы. Линейные операции с матрицами. Умножение матриц. Обратная матрица.

25. Элементарные преобразования матриц. Приведение матрицы к ступенчатому виду.

26. Пространство R n арифметических векторов (линейное пространство).

27. Линейная зависимость. Базис. Линейное подпространство в R n .

28. Размерность линейного подпространства (пространства). Ранг матрицы.

29. Системы линейных алгебраических уравнений. Матричные уравнения.

30. Системы n линейных алгебраических уравнений относительно n неизвестных. Правила Крамера.

31. Свойства решений линейной системы. Нетривиальная совместность однородной системы. Совместность линейной системы.

32. Фундаментальная система решений линейной однородной системы. Структура общего решения однородной системы.

33. Структура общего решения неоднородной системы.

34. Линейный оператор в R n (в линейном пространстве). Матрица линейного оператора.

35. Действия с линейными операторами и их матрицами.

36. Преобразование координат вектора и матрицы линейного оператора при изменении базиса.

37. Собственные значения и собственные векторы линейного оператора. Их свойства и вычисление.

38. Кривые 2-го порядка.

39. Поверхности 2-го порядка.

Экзаменационные задачи по МА

1. Найти производную если

2. Провести исследование и построить график функции:

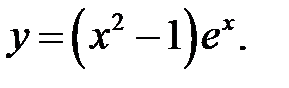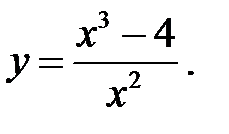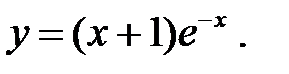Экзаменационные задачи по ЛА

1. Исследовать систему линейных алгебраических уравнений (доказать совместность, записать фундаментальную систему решений, найти и проверить общее решение):

2. Треугольник ABC задан координатами вершин: A(1,0,0), B(0,1,0), C(0,0,1). Вычислить площадь треугольника.

4. Записать уравнение грани тетраэдра OABC, где O(0,0,0), A(1,0,0), B(0,1,0), C(0,0,1) (достаточно одной).

5. Записать уравнения высоты тетраэдра OABC, опущенной из вершины С: (где O(0,0,0), A(1,0,0), B(0,1,0), C(0,0,1)).

7. Линейный оператор A, действующий в R 3 , задан матрицей A

Найти координаты образа вектора

8. Линейный оператор, действующий в R 2 , задан в некотором базисе матрицей

Найти матрицу оператора в базисе

9. Исследовать на линейную зависимость систему векторов:

10. Вычислить обратную матрицу. Провести проверку.

Основные свойства призмы

В данной публикации мы рассмотрим основные свойства призмы (касательно оснований, боковых ребер, граней и высоты), сопроводив их наглядными рисунками для лучшего восприятия представленной информации.

Примечание: определение призмы, ее основные элементы, разновидности и варианты сечения мы рассмотрели в отдельной публикации, поэтому здесь на них подробно останавливаться не будем.

Свойства призмы

Свойства будем рассматривать на примере шестиугольной прямой призмы, но они применимы к любому другому виду фигуры.

Свойство 1

Призма имеет два равных основания, которые являются многоугольниками.

Свойство 2

Свойство 3

Все боковые ребра призмы взаимно параллельны и равны.

Свойство 4

Перпендикулярное сечение призмы расположено под прямым углом ко всем боковым граням и ребрам фигуры.

Свойство 5

Высота (h) любой наклонной призмы всегда меньше длины ее бокового ребра. А высота прямой фигуры равна ее ребру.

Задачи по геометрии. 11 класс Планиметрия

Главная > Документ

Информация о документе
Дата добавления:
Размер:
Доступные форматы для скачивания:

1 . Найдите объем многогранника, вершинами которого являются середины ребер тетраэдра объемом V.

Решение . Многогранник получен отсечением от пирамиды четырех маленьких пирамид, объем каждой из которых равен , где S и H – площадь основания и высота исходной пирамиды, то есть маленькая пирамида имеет объем

2 . Шар касается всех ребер куба. Найдите площадь поверхности шара, лежащей внутри куба, если ребро куба равно 1.

Решение . Для того, чтобы существовал шар, касающийся всех ребер призмы, необходимо и достаточно, чтобы призма была правильной и все ее ребра были равными между собой. Идея доказательства: боковыми гранями должны быть параллелограммы, в которые можно вписать окружность (теорема о трех перпендикулярах), то есть ромбы (на самом деле – квадраты — почему?); спроектировав картину на плоскость основания, получим многоугольник с равными сторонами, вписанный в окружность, то есть – правильный многоугольник. Решаем нашу задачу. Более идеальной призмы, чем куб, нет, и центр шара является центром куба. Пусть R – радиус шара. . Наружу куба выходят 6 (по числу граней куба) шаровых сегментов. Если h – высота одного сегмента, то .

Ответ . .

3 . Сфера проходит через вершины одной грани куба и касается сторон противоположной грани куба. Найдите отношение объемов шара и куба.

Решение . ABCDA 1 B 1 C 1 D 1 – куб с ребром 1. Касание с ребрами противоположной грани происходит в их серединах (почему? Опустим перпендикуляры из центра сферы на грань и увидим конфигурацию теоремы о трех перпендикулярах. ). Воспользуемся методом координат, поместив начало в вершину A и направив оси сонаправленно сторонам AD, AB, AA 1 . Пусть O(a; b; c) – центр сферы, R – радиус, тогда (x-a) 2 + (y-b) 2 + (z-c) 2 = R 2 — ее уравнение. Получаем систему уравнений и решаем ее:

Ответ . .

4 . В сферу радиусом R вписана правильная треугольная призма со стороной основания a. Найдите площадь сечения призмы плоскостью, проходящей через центр сферы и сторону основания призмы.

Решение . На этом примере особенно удобно показать эффективность использования техники аналитической геометрии. Если бы мы знали угол между плоскостью сечения и гранью основания, то воспользовались бы теоремой о площади ортогональной проекции многоугольника, поскольку площадь основания ABC призмы ABCA 1 B 1 C 1 находится сразу. Но угол между плоскостями мы найдем, если сумеем записать уравнения этих плоскостей в какой-либо координатной системе. Теперь стратегия ясна. Во-первых, задаем систему координат с началом в центре O 1 правильного треугольника ABC: , O – центр сферы. Во-вторых, предаемся приятным (они простые) вычислениям: найдем вектор нормали к плоскости ABO, затем косинус угла между плоскостями ABO и ABC и после некоторых (опять же очевидных) выкладок напишем ответ. , . . Вот и

Ответ . .

5 . В треугольную пирамиду высотой 4, в основании которой лежит прямоугольный треугольник с гипотенузой 15, вписан конус, вершина которого совпадает с вершиной пирамиды, а основанием является вписанная в треугольник окружность с радиусом, равным 3. Найдите отношение площади полной поверхности конуса к площади полной поверхности пирамиды.

Решение . Боковые грани пирамиды SABC равнонаклонены к плоскости основания, а вершина S проектируется в центр O вписанной в треугольник ABC окружности. Решая систему , найдем AC = 9, BC = 12. Пусть D – точка касания с BC вписанной в ABC окружности. Образующая конуса SD перпендикулярна к OD (теорема о трех перпендикулярах) и является высотой грани SBC. Получается, что высоты всех боковых граней к ребрам основания пирамиды равны между собой (равны h); их найдем по теореме Пифагора: . . .

Ответ . .

6 . Основанием пирамиды является прямоугольник площади Q, две боковые грани перпендикулярны плоскости основания, а две другие образуют с ней углы и . Найдите объем пирамиды.

Решение . Грани SAB и SBC перпендикулярны основанию ABCD пирамиды SABCD, поэтому боковое ребро (теорема о трех перпендикулярах) и ; точно так же . .

Ответ . .

7 . Две взаимно перпендикулярные образующие конуса делят окружность его основания на дуги и . Найдите объем конуса, если его высота равна H.

Решение . Пусть R – радиус основания, l — образующая, d – хорда основания, стягивающая дугу в . Сразу получаем .

Ответ . .

8 . Высота усеченной пирамиды равна h, площадь среднего сечения равна S. В каких пределах может меняться объем пирамиды?

Решение . Основания и среднее сечение – подобные многоугольники. Пусть a, b, c – сходственные стороны этих многоугольников (a > b; c = (a + b) / 2), S 1 и S 2 – площади оснований.

; . — неравенство Коши о среднем арифметическом и среднем геометрическом. Кроме того, .

Ответ . .

9 . В шар радиуса R вписан параллелепипед наибольшего объема, отношение двух ребер которого равно 2 : 1. Найдите полную поверхность этого параллелепипеда.

Решение . Пусть x, 2x – два ребра “основания”, h – высота нашего параллелепипеда. Центр шара – середина диагонали параллелепипеда. Теперь – вычисления:

5×2 + H3 = 4R2, .

Ответ . .

10 . В каком отношении плоскость, проходящая через точки пересечения медиан треугольников ABC, ABD и BCD делит отрезок BD (ABCD — пирамида)?

Решение . , где M, N, P – центроиды граней ABD, BCD и ABC соответственно, — плоскость, проходящая через M, N, P; эта плоскость содержит векторы и . и z = 1/3, DK : KB = 1 : 2.

11 . Найдите радиус шара, описанного около пирамиды, все боковые ребра которой равны 5, а высота равна 4.

Решение . Центр O шара лежит на высоте SD пирамиды. E – середина AS. — равнобедренный, поэтому . В прямоугольном треугольнике ADS SD=4, AS=5. Треугольники EOS и ASD подобны и SO:AS = ES:SD, SO=R=25/8.

12 . Известно, что в заданную призму можно вписать шар. Найдите площадь ее боковой поверхности, если площадь основания равна S.

Решение . Высота призмы равна 2r, где r – радиус вписанного шара. .

13 . Осевым сечением конуса является равнобедренный прямоугольный треугольник с гипотенузой 2. Через вершину конуса проведено сечение, образующее угол с плоскостью основания. Найдите площадь этого сечения.

Решение . Катет = . (h – высота на гипотенузу); высота сечения = (это – ответ ).

14 . Через вершину прямого кругового конуса проведено сечение наибольшей площади. Площадь этого сечения в два раза больше площади осевого сечения конуса. Найдите угол при вершине осевого сечения конуса.

Решение . Пусть l – образующая. Угол при вершине больше прямого, иначе осевое сечение имело бы наибольшую площадь. В ситуации задачи наибольшую площадь имеет сечение, являющееся прямоугольным треугольником. .

Ответ . .

15 . Стороны треугольника равны a, b и c. Три шара попарно касаются друг друга и плоскости треугольника в его вершинах. Найдите радиусы этих шаров.

Решение . , .

Ответ . .

16 . Два шара с радиусами 2 и 3 имеют центры в точках A и B соответственно, AB = 7. Плоскость, касающаяся этих шаров, пересекает прямую AB в точке M. Найдите AM.

Решение . Подобные треугольники: два случая. 1) ;

2) .

17 . Точки M, N и P – середины ребер AB, CD и BC тетраэдра ABCD. Через точку P проведена плоскость, параллельная DM и AN. В каком отношении эта плоскость делит ребро AD?

Решение . Пусть — плоскость, о которой говорится в задаче. Если векторы и отложить от точки P, то они будут лежать в плоскости . . Векторы некомпланарны; разложим по ним , , то есть .

Ответ . AQ : QD = 1 : 1.

18 . В прямоугольном параллелепипеде ABCDA 1 B 1 C 1 D 1 из вершин A 1 и B опущены перпендикуляры A 1 P и BQ на диагональ AC 1 . Найдите длину отрезка PQ, если AB=a, AD=b, AA 1 =c.

Решение . , . Аналогично .

Ответ . .

19 . Условия существования описанной около призмы сферы:

1) призма прямая;

2) около основания можно описать окружность.

Решение полезно провести самостоятельно или заглянуть в учебник.

20 . Условия существования вписанной в призму сферы:

1) в перпендикулярное сечение можно вписать окружность;

2) высота призмы равна диаметру этой окружности.

Решение . См. задачу 19.

21 . В полусферу радиуса R вписан куб так, что четыре его вершины лежат на основании полусферы, а остальные четыре – на сферической поверхности. Найдите объем куба.

Решение . Нужно отразить всю конструкцию относительно плоскости основания полусферы и получить

Ответ . .

22 . Теорема . Около пирамиды можно описать сферу, если около многоугольника основания можно описать окружность. Это – критерий.

Доказательство . Надо вспомнить определение центра описанной около многогранника сферы.

23 . Пусть — двугранный угол при ребре основания (усеченной) правильной пирамиды или угол наклона образующей (усеченного) конуса к плоскости основания, S 1 и S 2 – площади нижнего и верхнего основания пирамиды (конуса). Тогда боковая поверхность S пирамиды (конуса) равна .

Доказательство . Теорема о площади ортогональной проекции поверхности; если пирамида (конус) не усеченная (усеченный), то S 2 =0.

24 . Основание пирамиды – ромб с острым углом . Боковые грани наклонены к плоскости основания под углом . Радиус вписанного в ромб круга равен r. Найдите полную поверхность пирамиды.

Решение . Применим результат задачи 23. = (a – сторона ромба); .

Ответ . .

25 . Сторона основания правильной треугольной пирамиды равна a, а боковое ребро равно b. Найдите радиус сферы, касающейся всех ребер пирамиды.

Решение . Пусть в пирамиде SABC SK – высота, а O — центр нашей сферы. . Ребра SA и SB симметричны относительно плоскости SDC, проходящей через центр сферы, = диаметральной плоскости, значит (здесь нужна запятая, но в контексте математических рассуждений это не принято) центр O лежит на высоте пирамиды. BM = BD = a/2 (касательная из точки B к сфере). Треугольники SOM и SBK подобны. См. задачу 31.

Ответ . .

26 . SABCD – правильная четырехугольная пирамида. Двугранный угол при ребре основания равен . Через ребро AB = a основания проведена плоскость под углом к основанию. Найдите площадь сечения.

Решение . ABMK – сечение, ABM 1 K 1 – ортогональная проекция сечения на плоскость ABCD – равнобочная трапеция, угол между диагоналями которой равен (поскольку точки M и K проектируется в точки диагоналей AC и BD квадрата ABCD) ; (O – точка пересечения диагоналей основания); из подобия треугольников SOD и KK 1 D получим (здесь точка P – основание перпендикуляра из O на AB):

, .

Ответ . .

27 . Имеется плоскость и прямая l, перпендикулярная . Найдите множество центров шаров радиуса r, касающихся плоскости и прямой l.

Решение . Построим две плоскости (по разные стороны от ), расстояние которых до равно r. В них на расстояние r до l удалены точки окружностей радиуса r с центрами в точках пересечения прямой l с этими плоскостями.

28 . Через вершину конуса проведено сечение, имеющее наибольшую площадь. Плоскость этого сечения составляет с плоскостью основания угол . Образующая конуса равна l. Найдите объем меньшей части конуса, отсеченной этой плоскостью.

Решение . Указанное сечение – не осевое; угол между образующими в этом сечении прямой. Пусть ABS – это сечение. . и AB – сторона правильного треугольника, поэтому ASB – грань правильной треугольной пирамиды, вписанной в конус, причем боковые ребра попарно перпендикулярны.

Ответ . .

29 . В наклонной призме ABCDA 1 B 1 C 1 D 1 AC = 5, BD = 4, AC и BD перпендикулярны. Диагональное сечение BB 1 D 1 D — прямоугольник. . Найдите объем призмы.

Решение . BB 1 D 1 D – прямоугольник высота призмы лежит в плоскости диагонального сечения .

30 . В тетраэдре ABCD двугранные углы при ребрах AB, AC и BD прямые. Один из отрезков, соединяющих середины противоположных ребер тетраэдра, имеет длину a, другой – длину . Найдите длину наибольшего ребра тетраэдра.

Решение . Задача трудная, она предлагалась на вступительном экзамене в МФТИ в 1979 году, когда геометрия считалась (и была) обязательным элементом математической культуры. Решаем. . Применим теорему косинусов для трехгранного угла ADBC: . Теперь – координаты! Пусть P, Q, M, N, R, S – середины ребер AB, DC, AD, BC, DB, AC соответственно. Тогда A(0;0;0), B(x;0;0), C(x;y;0), D(0;0;z), P(x/2;0;0), Q(x/2;y/2;z/2), M(0;0;z/2), N(x;y/2;0), R(x/2;0;z/2), S(x/2;y/2;0). Используем условие задачи: PQ 2 = RS 2 = (y 2 + z 2 )/4 = a 2 , MN 2 = x 2 + (y 2 + z 2 )/4 = 6a 2 . Выбирая наибольшее ребро, получим x 2 + y 2 + z 2 = AC 2 + AD 2 = CD 2 = 5a 2 + 4a 2 = 9a 2 .

31 . Найдите радиус шара, касающегося всех ребер правильной треугольной пирамиды, у которой сторона основания равна 2, а боковое ребро равно 3.

Решение . Шар касается ребер. Нестандартная для восприятия конфигурация. Шар протыкает поверхность пирамиды. Радиус шара (r) перпендикулярен к ребру в точке касания. Проведем из центра O шара перпендикуляры OO 1 и OO 2 к граням ABC и BDC пирамиды DABC; равным наклонным (радиусы шара) соответствуют равные проекции, то есть шар пересекает грани по вписанным в них кругам. Центр шара лежит на высоте тетраэдра. Пусть P (M) – точка касания шара с ребром BC (BD), r 1 и r 2 – радиусы кругов, вписанных в треугольники ABC и BDC, H — высота пирамиды (O 1 D). Радиусы r 1 и r 2 легко вычисляются (метод площадей). OO 1 = a, тогда OD = H – a. Из треугольников OO 1 P и OMD получаем . И т.д.

Другой способ : ввести систему координат с началом O 1 ; O 1 C- ось ординат. Вычислив координаты всех нужных точек и написав уравнения нужных плоскостей, придем к тому же, только усилия будут перенесены на алгебру.

Ответ . . См. задачу 25.

32 . Ребро куба ABCDA 1 B 1 C 1 D 1 равно a. Найдите радиус сферы, проходящей через середины ребер AA 1 , BB 1 и через вершины A и C 1 .

Решение . Умение увидеть геометрическую картину и смело использовать координатную технику – вот чему особенно важно научиться в процессе знакомства с геометрией. Без колебаний связываем с кубом ABCDA 1 B 1 C 1 D 1 систему координат: A(0;0;0), …, C 1 (a;a;a). O(x 0 ;y 0 ;z 0 ) – центр сферы, P(0;0;a/2) и Q(0;a;a/2) — середины ребер AA 1 и BB 1 . Используя уравнение искомой сферы радиуса R, решаем систему уравнений

и т.д.

Ответ . .

33 . Основанием призмы ABCDA 1 B 1 C 1 D 1 является ромб с острым углом и стороной a. Вершина A 1 призмы удалена на расстояние a от вершин A, B и D. Найдите: а) площадь диагонального сечения BB 1 D 1 D; б) объем призмы.

Решение . AA 1 D и AA 1 B — равные равносторонние треугольники, следовательно, углы A 1 AD и A 1 AB равны и (по теореме о трехгранном угле с двумя равными плоскими углами) A 1 проектируется в точку O биссектрисы угла BAD ромба ABCD; если , то (теорема о трех перпендикулярах). Но в правильном треугольнике A 1 AD A 1 E – медиана, поэтому и высота призмы . Все по той же теореме о трех перпендикулярах, ; таким образом, сечение BB 1 D 1 D – прямоугольник со сторонами .

Ответ . ; .

34 . Шар радиуса r касается всех ребер тетраэдра. Центр шара лежит внутри пирамиды на ее высоте на расстоянии от вершины. Найдите высоту пирамиды.

Решение . Задача предлагалась на вступительном экзамене на мехмат МГУ. Ключ к решению: если центр касающегося всех ребер пирамиды шара лежит на ее высоте, то пирамида – правильная. Идея доказательства: прямоугольные треугольники SOP 1 , SOP 2 ,… (S – вершина пирамиды, O – центр шара, P 1 , P 2 , . – точки касания с боковыми ребрами) равны по гипотенузе (SO) и катету (OP 1 , OP 2 ,…), поэтому боковые ребра SA 1 , SA 2 , … образуют равные углы с высотой SH пирамиды, но они же – острые углы в равных прямоугольных треугольниках SHA 1 , SHA 2 , … (у них общий катет SH, прилегающий к этим углам); получаем HA 1 = HA 2 = …, то есть H – центр описанной около основания окружности; кроме того, H – центр вписанной в основание окружности (здесь вопрос решается теоремой о трех перпендикулярах), следовательно, многоугольник основания – правильный (почему?). Приступаем к вычислениям. Пусть OH=x, AB = a, R впис. (R опис. ) – радиус вписанной в основание (описанной около основания) ABC окружности.

Ответ . .

35 . В правильной четырехугольной пирамиде площадь боковой грани равна Q, боковая грань наклонена к плоскости основания под углом . Найдите объем пирамиды.

Решение . Теорема о площади ортогональной проекции: (a – сторона основания), (h — высота пирамиды).

Ответ . .

36 . Диагонали осевого сечения усеченного конуса взаимно перпендикулярны, равны d и делят друг друга в отношении 1 : 3. Найдите объем конуса.

Решение . Пусть r – радиус меньшего основания конуса. Тогда радиус большего основания равен 3r (из подобия треугольников). Пришло время интегрировать! Вводим прямоугольные координаты. Конус получается вращением прямоугольной трапеции с границами 0 и 4r по Ox и 0 и r по Oy вокруг оси Ox. Уравнение боковой стороны (верхней границы интегрирования): . Интегрируем:

Ответ . .

37 . Треугольная пирамида, боковые ребра которой попарно перпендикулярны и равны a, вписана в конус так, что одно боковое ребро является высотой конуса, а две вершины лежат на основании конуса. Найдите а) отношение объема конуса к объему пирамиды;

б) отношение поверхности конуса к поверхности пирамиды.

Решение . Пусть SABC – пирамида; A – вершина, AS – высота, BSC – плоскость основания конуса, вершины B и C пирамиды лежат на основании конуса; S – центр, a – радиус основания конуса. По условию, SA, SB и SC попарно перпендикулярны.

. . Треугольник ABC – равносторонний со стороной , , .

Ответ . .

38 . Основанием пирамиды SABC является равнобедренный треугольник ABC (AC=BC=a) с углом . Боковая грань SAB перпендикулярна к основанию, а две другие наклонены к основанию под углом . Найдите объем пирамиды.

Решение . . С другой стороны, точка S проектируется на биссектрису угла ACB (теорема о трехгранном угле с двумя равными плоскими углами) (CD – биссектриса угла ACB равнобедренного треугольника ACB) и D – середина AB. Если , то . Пусть BP – высота треугольника ACB, тогда DE легко находится как средняя линия треугольника ABP: . Из треугольника SDE: .

Ответ . .

39 . В четырехугольной пирамиде SABCD, основанием которой является параллелограмм ABCD, проведено сечение через ребро AB и середину M ребра SC. Найдите отношение объемов частей, на которые сечение разделило пирамиду.

Решение . , где , . (SBCD и SAMN – треугольные пирамиды с общей вершиной B). . Рассмотрим пирамиды SBAN и SBAD; за основания примем грани SAN и SAD, а точку B – за общую вершину этих пирамид. .

40 . Какой наибольший объем может иметь четырехугольная пирамида, боковое ребро которой имеет длину 1?

Решение . Пирамида с равными боковыми ребрами обладает следующими свойствами:

а) боковые ребра равнонаклонены к плоскости основания; б) около основания (у нас – четырехугольник) можно описать окружность; в) вершина пирамиды проектируется в центр этой окружности. Зафиксируем на время угол наклона бокового ребра к грани основания, тогда высота пирамиды и радиус описанной около основания окружности будут равны соответственно и , и объем пирамиды будет пропорционален площади основания, вписанного в окружность фиксированного радиуса. Наибольшую площадь в рассматриваемой ситуации имеет квадрат: если — последовательные угла между парами радиусов окружности, то площадь вписанного четырехугольника пропорциональна , а эта сумма принимает наибольшее значение при , то есть все углы прямые (основание – квадрат). Предположим теперь, что мы достигли цели и обнаружили пирамиду с наибольшим объемом. Тогда, если основанием является не квадрат, можно при той же высоте (том же угле наклона бокового ребра к основанию) вписать в упомянутую окружность квадрат, принять его за основание новой пирамиды и тем самым увеличить объем. Приведенными рассуждениями установлено, что основанием нашей пирамиды должен быть квадрат. Дальнейшее просто. Площадь основания равна , объем равен . Исследуя эту функцию на экстремум, находим, что .