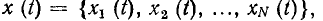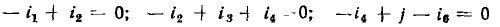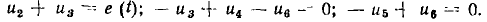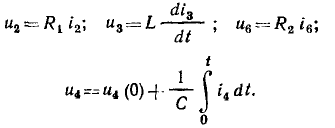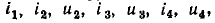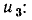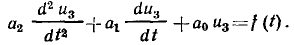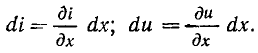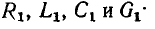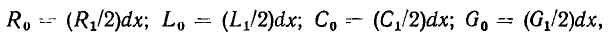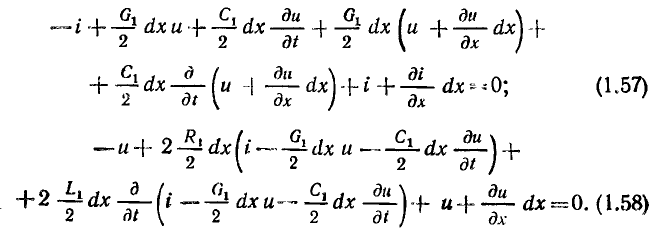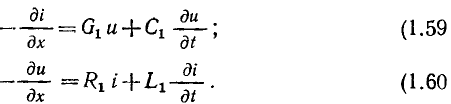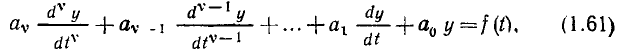Запишите уравнение электрического состояния цепи

Комплексные уравнения электрического состояния цепи.

Электрическое состояние цепей синусоидального тока, так же как и цепей постоянного тока, описывается с помощью уравнений, составленных в соответствии с законами Кирхгофа.

В общем виде тригонометрическое уравнение по первому закону Кирхгофа для узла цепи синусоидального тока имеет вид

, (57)

где n – число ветвей, сходящихся в узле.

Этому уравнению соответствует уравнение первого закона Кирхгофа в комплексной форме (например, для действующих значений)

. (58)

Правила знаков при составлении уравнений (58) остаются теми же, что и в цепях постоянного тока: токи, положительные направления которых направлены от узла, следует брать со знаком минус, а токи, положительные направления которых направлены к узлу – со знаком плюс.

Для любого контура цепи с синусоидальными напряжениями справедливо тригонометрическое уравнение, составленное по второму закону Кирхгофа.

В идеализированных электрических цепях магнитное поле считается сосредоточенным только на участках цепи, содержащих индуктивные элементы. При обходе замкнутого контура цепи всегда можно выбрать путь, лежащий вне переменного магнитного поля, а участок, содержащий индуктивный элемент, характеризовать разностью потенциалов, т. е. напряжением на его зажимах; при этом изменение потенциала в любом замкнутом контуре цепи синусоидального тока равно нулю. Поэтому, согласно второму закону Кирхгофа, алгебраическая сумма мгновенных значений напряжений всех участков замкнутого контура равна нулю:

, (59)

где m — число участков, рассматриваемого контура.

Тригонометрическое уравнение можно заменить соответствующим ему комплексным уравнением второго закона Кирхгофа (например, для действующих значений)

. (60)

Применительно к схемам замещения с источниками ЭДС второй закон Кирхгофа можно сформулировать таким образом: алгебраическая сумма комплексных напряжений на пассивных элементах замкнутого контура равна алгебраической сумме сторонних ЭДС, входящих в этот контур:

. (61)

Правила знаков при составлении уравнений (60) и (61) остаются теми же, что и в цепях постоянного тока: слагаемые берут со знаком плюс в случае, когда направление обхода совпадает со стрелкой положительного направления соответственно напряжения, тока или ЭДС.

Последовательное соединение элементов в цепи синусоидального тока.

Рассмотрим в качестве примера цепь с последовательным включением резистора, индуктивной катушки и конденсатора. Такая цепь с достаточной точностью описывается схемой замещения, представленной на рисунке 13. Найдем связь между напряжением на входе цепи и током , используя комплексные числа.

Запишем уравнение по второму закону Кирхгофа в комплексной форме:

. (62)

Выразим слагаемые правой части уравнения через комплексное значение тока , воспользовавшись записью закона Ома в комплексной форме для каждого из элементов цепи:

и перепишем (62) в виде

. (63)

Соотношение (63) является записью закона Ома рассматриваемой цепи в комплексной форме, а комплекс 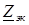– эквивалентным комплексным сопротивлением цепи:

. (64)

Таким образом, при последовательном соединении элементов цепи эквивалентное комплексное сопротивление цепи равно сумме комплексных сопротивлений всех последовательно включенных элементов, т. е. правило определения эквивалентного комплексного сопротивления последовательной цепи совпадает с аналогичным правилом для цепи постоянного тока. Очевидно, полученный результат справедлив для цепи с последовательным включением любого числа элементов.

Пример расчёта цепи синусоидального тока.

Произведём расчёт токов цепи синусоидального тока, представленной на рисунке 14.

, (65)

где — промышленная частота.

Токи в схеме рисунка 14 можно рассчитать любым методом, аналогичным образом как для цепи постоянного тока.

Метод контурных токов.

В схеме рисунка 14 задаём направление неизвестных токов. Также выбираем направление контурных токов (например, по часовой стрелке). В схеме рисунка 14 можно выделить три контурных тока. Последовательные соединения 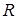-, -, — элементов заменяем на эквивалентные. Результаты произведённых действий представлены на рисунке 15.

Для схемы рисунка 15 получаем эквивалентные сопротивления

, (66)

источники ЭДС в комплексной форме

. (67)

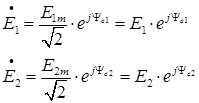
Для определения контурных токов необходимо составить следующую систему уравнений:

. (68)

Уравнения для контурных токов можно записать в матричной форме:

(69)

. (70)

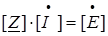
Решением уравнения (70) будет

. (71)

Далее необходимо определить неизвестные токи через контурные токи:

(72)

Метод узловых потенциалов.

Аналогичным образом, как в методе контурных токов, представляем исходную схему в виде, представленном на рисунке 16.

В схеме (рисунок 16) потенциал . Для определения токов необходимо составить систему уравнений, неизвестными которой являются потенциалы узлов. Данная система составляется следующим образом:

. (73)

Уравнения для узловых потенциалов (73) можно записать в матричной форме:

. (74)

, (75)

где — матрица узловых и взаимных проводимостей, — матрица узловых токов, — матрица неизвестных потенциалов.

Решением уравнения (75) будет

. (76)

Далее определяются токи

(77)

Баланс мощности.

Потребляемая полная мощность:

(78)

где — активная мощность, а — реактивная мощность.

Полная мощность источников:

, (79)

где и — комплексно сопряжённые токи.

Потенциальная диаграмма.

Построим потенциальную диаграмму для левого контура, представленного на рисунке 17, исходной схемы (рисунок 14).

На данном примере (рисунок 17) получаем

(80)

Если потенциалы (80) перенести на комплексную плоскость, то должна получиться замкнутая траектория. При этом, потенциал .

№74 Расчет переходных процессов методом переменных состояния.

Уравнениями состояния электрической цепи называют любую систему дифференциальных уравнений, которая описывает состояние (режим) данной цепи. Например, система уравнений Кирхгофа является уравнениями состояния цепи, для которой она составлена.

В более узком смысле в математике уравнениями состояния называют систему дифференциальных уравнений 1-го порядка, разрешенных относительно производных (форма Коши). Система уравнений состояния в обобщенной форме имеет вид:

Та же система уравнений в матричной форме:

или в обобщённой матричной форме:

Система уравнений состояния формы Коши решается методом численного интегрирования (метод Эйлера или метод Рунге-Кутта) на ЭВМ по стандартной программе, которая должна быть в пакете стандартных программ. При отсутствии такой программы в пакете она легко может быть составлена по следующему алгоритму (метод Эйлера) для к-го шага:

Значения производных на к-ом шаге:

Значения переменных на к-ом шаге:

Для определения значений переменных и их производных на 1-м шаге ин¬тегрирова¬ния используются их значения на момент t=0, т.е. их начальные условия x1(0), x2(0). xn(0).

Уравнения состояния формы Коши для заданной схемы могут быть получены из системы уравнений Кирхгофа путем их преобразования. Для этой цели: а) из системы уравнений Кирхгофа методом подстановки исключаются »лишние» переменные, имеющие зависимые начальные условия, и оставляют переменные iL(t) и uC(t), которые не изменяются скачком и имеют независи-мые начальные условия iL(0) и uC(0); б) оставшиеся уравнения решаются относительно производных и приводятся их к форме Коши.

В случае сложных схем уравнения состояния формы Коши могут быть составлены топологическими методами с использованием матриц соединений [A] и [B].

Последовательность расчета переходного процесса методом переменных состояния выглядит так:

1. Производится расчет схемы в установившемся режиме до коммутации и определяются независимые начальные условия iL(0) и uC(0).

2. Составляется система дифференциальных уравнений по законам Кирхгофа для схемы после коммутации.

3. Методом исключения »лишних» переменных система уравнений Кирхгофа преобразуется в систему уравнений Коши, составляются матрицы коэффициентов.

4. Выбирается расчетное время (продолжительность переходного процесса) и число шагов интегрирования N.

5. Решение задачи выполняется на ЭВМ по стандартной программе. Выходную функцию получают в виде графической диаграммы x=f(t)или в виде таблицы координат функций для заданных моментов времени.

Пример. Для схемы рис. 74.1 с заданными параметрами элементов (e(t)=Emsin(ωt+ψE), R, R1, R2, R3, L1, L2, C) выполнить расчет переходного процесса и определить функцию uab(t).

1. Выполняется расчет схемы в установившемся режиме переменного тока до коммутации и определяются начальные условия i1(0), i2(0), uC(0).

2. Составляется система дифференциальных уравнений по законам Кирхгофа:

3. Система уравнений Кирхгофа преобразуется в систему уравнений Коши.

Для этой цели из (1) выражаем

и делаем подстановку в (1) и (2), а из (4) делаем подстановку в (1). Тогда получим:

Подсчитаем значения отднльных коэфициэнтов:

Составляем матрицы коэффициентов:

В качества исследуемого промежутка времени выбираем период переменного тока

Число шагов интегрирования принимаем N = 1000,

Вводим исходные данные в ЭВМ и выполняем рассчет.

В качестве выходной функции принимаем:

Для выходной функции Uab(T) строим графическую диаграмму в интервале периода Т.

Уравнения электрического равновесия цепей

Содержание:

Уравнения электрического равновесия цепей:

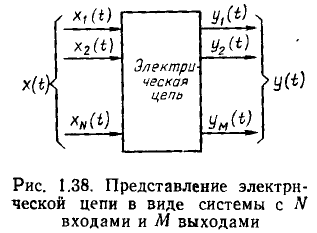
Любую электрическую цепь можно рассматривать как систему с одним или несколькими входами и одним или несколькими выходами (рис. 1.38). Если к входам цепи приложить внешнее воздействие

Задача анализа электрической цепи состоит в определении реакции цепи у (t) на заданное внешнее воздействие х (t).

Задача синтеза цепи заключается в нахождении цепи по заданной реакции цепи у (t) на некоторое внешнее воздействие х (t).

Исходными данными в задаче анализа являются эквивалентная схема цепи с параметрами всех входящих в нее элементов и описание внешнего воздействия х (t), задаваемого в виде совокупности токов и напряжений идеализированных неуправляемых источников. В результате анализа определяется отклик у (t) в виде совокупности токов и напряжений всех или некоторых ветвей цепи. В частном случае задача анализа может сводиться к определению соотношений между реакциями цепи на отдельных выходах и воздействиями приложенными к определенным входам. Такие соотношения называются характеристиками (системными функциями, функциями) цепи. В зависимости от того, какая величина— частота или время — является аргументом в выражениях, описывающих соотношения между откликом и внешним воздействием, различают частотные и временные характеристики цепи. Определение и исследование частотных характеристик представляют собой задачу анализа цепи в частотной области; нахождение временных характеристик — задачу анализа цепи во временной области.

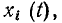
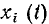
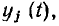
Исходными данными в задаче синтеза являются описания внешнего воздействия х (t) и ее отклика у (t). В результате синтеза необходимо найти эквивалентную схему цепи и параметры всех входящих в нее элементов. В частном случае задача синтеза может сводиться к нахождению цепи, обеспечивающей заданные соотношения между внешним воздействием на цепь и ее реакцией т. е. к нахождению цепи по ее характеристикам.

Анализ и синтез электрических цепей в определенной степени взаимосвязаны, в частности методы синтеза базируются на использовании общих свойств характеристик различных классов цепей, которые изучаются в процессе анализа. Поэтому изложению методов синтеза цепей будет предшествовать рассмотрение общих методов анализа цепей и знакомство с характеристиками некоторых классов цепей при различных внешних воздействиях.

Понятие об уравнениях электрического равновесия

Математически задача анализа электрической цепи сводится к составлению и решению системы линейно независимых уравнений, в которых в качестве неизвестных фигурируют токи и напряжения ветвей исследуемой цепи. Уравнения, решение которых позволяет определить токи и напряжения ветвей электрической цепи, называются уравнениями электрического равновесия цепи. Очевидно, что число уравнений электрического равновесия должно быть равно количеству неизвестных токов и напряжений.

В общем случае в цепи, содержащей р ветвей и q узлов, имеется 2р неизвестных токов и напряжений ветвей. Используя законы Кирхгофа, для такой цепи можно составить m = q— 1 независимых уравнений баланса токов и n = р — q + 1 независимых уравнений баланса напряжений. В сочетании с компонентными уравнениями (уравнениями ветвей) получаем 2р линейно независимых уравнений, что достаточно для определения неизвестных токов и напряжений ветвей.

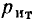
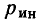
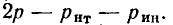
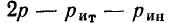
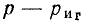
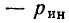
Если в рассматриваемой цепи имеется ветвей, в которых содержатся идеализированные источники тока (токи этих ветвей заданы, а напряжения неизвестны), и ветвей, составленных только из идеализированных источников напряжения (напряжения этих ветвей известны), то общее число неизвестных токов и напряжений уменьшается до Для определения этих неизвестных нужно составить лишь линейно независимых уравнений (m + n = р уравнений на основании законов Кирхгофа и компонентных уравнений для ветвей, не содержащих указанных источников).

Таким образом, используя компонентные уравнения и топологические уравнения, составленные на основании законов Кирхгофа, всегда можно сформировать систему уравнений электрического равновесия, число уравнений в которой достаточно для определения всех неизвестных токов и напряжений. Будем называть такую систему уравнений основной системой уравнений электрического равновесия цепи.

На практике для анализа цепей используют различные методы составления уравнения электрического равновесия, в частности методы токов ветвей, напряжений ветвей, контурных токов, узловых напряжений, переменных состояния. Все они базируются на использовании различных приемов, позволяющих преобразовать основную систему уравнений электрического равновесия и уменьшить по сравнению с 2р или 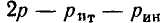число одновременно решаемых уравнений.

Как было показано ранее, уравнения (1.37) и (1.40) являются алгебраическими, а компонентные уравнения идеализированных пассивных элементов могут быть как алгебраическими (1.9), (1.10), так и дифференциальными (1.13), (1.22) или интегральными (1.16), (1.23).

Вследствие этого уравнения электрического равновесия цепи, составленные любым методом, представляют собой в общем случае систему интегродифференциальных уравнений.

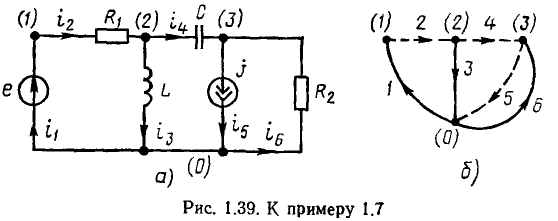
Пример 1.7.

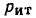
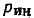
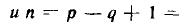
Составим основную систему уравнений электрического равновесия цепи, схема и топологический граф которой изображены на рис. 1.39, а и б соответственно. Для этой цепи р=6, q = 4, — 1 и = 1. Общее число неизвестных токов и напряжений ветвей Используя законы Кирхгофа, можно составить m = q — 1 = 3, уравнения баланса токов:

3 уровня баланса напряжений:

Кроме того, имеем 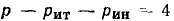уравнений ветвей, нес одержащих идеализированных источников:

В результате получаем систему из 10 линейно независимых уравнений для определения 10 неизвестных токов и напряжений:

Система уравнений электрического равновесия цепи, составленная любым методом, может быть путем дифференцирования и последовательного исключения неизвестных сведена к одному дифференциальному уравнению для любого из неизвестных токов и напряжений, называемому дифференциальным уравнением цепи. В частном случае это может быть алгебраическое уравнение, которое можно рассматривать как дифференциальное уравнение нулевого порядка. Дифференциальное уравнение цепи содержит фундаментальную информацию о характере имеющих место в цепи электрических процессов и является основой для классификации электрических цепей.Тип дифференциального уравнения цепи полностью определяется ее топологией и характером входящих в нее идеализированных элементов.

Пример 1.8.

Применяя указанные преобразования к основной системе уравнений электрического равновесия цепи (рис. 1.39, а), получим дифференциальное уравнение этой цепи, составленное относительно напряжения

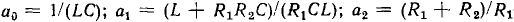
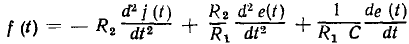
Здесь —постоянные коэффициенты, определяемые параметрами пассивных элементов цепи;

— Функция времени, определяемая параметрами независимых источников напряжения и тока.

Таким образом, уравнение цепи, изображенной на рис. 1.39, является линейным неоднородным дифференциальным уравнением 2-го порядка с постоянными коэффициентами

Классификация электрических цепей

Электрические цепи, составленные из идеализированных элементов, могут быть классифицированы по ряду признаков:

по топологическим особенностям: планарные (плоские) и непланарные (объемные), разветвленные и неразветвленные, простейшие (одноконтурные, двухузловые) и сложные (многоконтурные, многоузловые);

по энергетическим свойствам: активные (содержащие идеализированные активные элементы) и пассивные (не содержащие идеализированных активных элементов);

по числу внешних выводов: двухполюсники и многополюсники; и др.

Классификация цепей по этим признакам не носит принципиального характера и используется, в основном, с целью упорядочения терминологии.

Фундаментальный характер имеет классификация цепей в зависимости от вида дифференциального уравнения цепи. Идеализированные электрические цепи, процессы в которых описываются обыкновенными дифференциальными уравнениями, называются цепями с сосредоточенными параметрами. Цепи такого типа используют в качестве упрощенных моделей реальных электрических цепей и их элементов на сравнительно низких частотах, когда длина волны электромагнитных колебаний существенно больше размеров исследуемого устройства. При этих условиях в исследуемых устройствах и их элементах удается выделить конечное число’ участков, в которых преобладает какой-то один из основных эффектов — запасание энергии электрического или магнитного полей, преобразование электрической энергии в другие виды энергии или преобразование энергии сторонних сил в электрическую. Токи рассматриваемой реальной цепи, являясь функциями времени, имеют одинаковые мгновенные значения в пределах каждого из выделенных участков. Заменяя эти участки идеализированными активными или пассивными элементами, получают идеализированную цепь, содержащую конечное число элементов, значения параметров которых конечны.

Таким образом, цепи с сосредоточенными параметрами представляют собой идеализированные цепи, моделирующие реальные устройства или их элементы при условиях, когда можно предположить, что каждый из основных электрических эффектов сосредоточен в конечном числе пространственно локализуемых областей.

Когда длина волны электромагнитных колебаний соизмерима с размерами исследуемого устройства или его элементов, пространственно локализовать области, в которых сосредоточены только эффекты одного типа, не удается. Это связано с тем, что даже при бесконечно малой длине выделяемых участков, в пределах каждого из них имеют место одновременно несколько из перечисленных основных эффектов, причем значения токов в пределах выделенных участков изменяются от одного сечения к другому.

При этих условиях цепи, моделирующие реальные устройства или их элементы, содержат бесконечно большое число идеализированных элементов, параметры которых имеют бесконечно малые значения. Процессы в таких цепях описываются дифференциальными уравнениями в частных производных. Идеализированные электрические цепи, процессы в которых описываются дифференциальными уравнениями в частных производных, называются цепями с распределенными параметрами.

Следует подчеркнуть, что термины «цепь с распределенными параметрами» и «цепь с сосредоточенными параметрами» применимы только к идеализированным (моделирующим) цепям и не должны использоваться для характеристики реальных цепей.

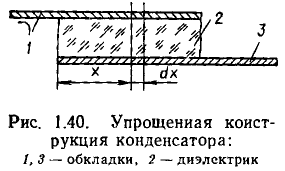
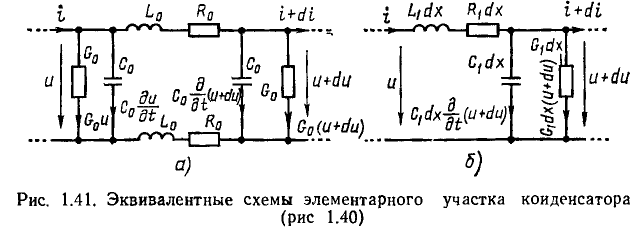
В зависимости от условий и требуемой точности исследования каждый элемент реальной цепи и, следовательно, каждая реальная цепь в целом могут быть заменены моделирующей цепью с сосредоточенными или распределенными параметрами. Например, конденсатор любого типа конструктивно представляет собой две проводящие обкладки 1 и 3, разделенные слоем диэлектрика 2 (рис. 1.40). В области частот, когда длина волны электромагнитных колебаний значительно превышает геометрические размеры обкладок, он может быть представлен одной из моделирующих цепей с сосредоточенными параметрами, схемы которых приведены на рис. 1.11. На более высоких частотах, когда длина волны электромагнитных колебаний сравнима с геометрическими размерами обкладок, но существенно больше расстояния между ними, необходимо учитывать, что процессы запасания энергии электрического и магнитного полей, а также необратимое преобразование электрической энергии в другие виды энергии имеют место вдоль всей длины обкладок конденсатора. 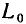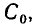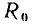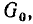В этом случае эквивалентная схема элементарного участка конденсатора длиной dx состоит из индуктивности и емкости характеризующих процессы запасания энергии магнитного и электрического полей, а также сопротивления и проводимости утечки учитывающих потери энергии в конденсаторе (рис. 1.41, а). Эквивалентная схема всего конденсатора должна состоять из бесконечно большого числа таких секций. Следовательно, идеализированная цепь, моделирующая конденсатор в рассматриваемом диапазоне частот, представляет собой цепь с распределенными параметрами.

На примере цепи, эквивалентная схема которой изображена на рис. 1.41, а, покажем, что электрические процессы в цепях с распределенными параметрами описываются дифференциальными уравнениями в частных производных. Действительно, ток i = i (х, t) и напряжение u = u (х, t) рассматриваемой цепи являются функциями времени t и координаты х.

Приращения тока и напряжения на участке цепи длиной dx

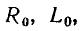
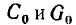
Полагая, что параметры элементов моделирующей цепи не зависят от токов и напряжений и выражая их через погонные (т. е. приходящиеся на единицу длины) параметры

составим уравнения баланса токов и напряжений элементарного участка цепи:

Пренебрегая величинами второго порядка малости, уравнения (1.57), (1.58) можно преобразовать к виду

Решая уравнения (1.59), (1.60) при соответствующих начальных граничных условиях, можно определить токи и напряжения цепи моделирующей коденсатор в рассматриваемом режиме.

Отметим, что уравнениям (1.59), (1.60) может быть поставлена в соответствие более простая эквивалентная схема элементарного участка цепи (рис. 1.41, б). Аналогичный вид имеют высокочастотные схемы замещения и ряда других элементов, входящих в состав радиоэлектронных устройств, в частности двухпроводных и коаксиальных линий передачи.

В зависимости от числа координат, вдоль которых происходит изменение тока и напряжения и вдоль которых «распределены» параметры цепи, различают одномерные, двухмерные и трехмерные цепи с распределенными параметрами. В теории цепей рассматривают, в основном, одномерные цепи с распределенными параметрами, процессы в которых описываются дифференциальными уравнениями типа (1.59), (1.60).

Параметры рассмотренных ранее идеализированных линейных пассивных элементов не зависят от значений токов и напряжений соответствующих элементов и, следовательно, от интенсивности внешнего воздействия на цепь, определяемой токами действующих в цепи независимых источников тока и напряжениями действующих в цепи независимых источников напряжения. Связь между током и напряжением линейных идеализированных пассивных элементов описывается линейными алгебраическими, дифференциальными или интегральными уравнениями, иными словами, компонентные уравнения этих элементов являются линейными.

Параметры нелинейных пассивных элементов зависят от токов или напряжений соответствующих элементов, а следовательно, и от интенсивности внешнего воздействия. Компонентные уравнения нелинейных идеализированных пассивных элементов — нелинейные.

В зависимости от вида компонентного уравнения идеализированные активные элементы также делятся на линейные и нелинейные. К линейным идеализированным активным элементам относят независимые в линейно управляемые зависимые источники тока и напряжения, к нелинейным — нелинейно управляемые зависимые источники тока г напряжения.

Цепь с сосредоточенными или распределенными параметрами, составленная только из линейных идеализированных элементов, называется линейной. Дифференциальное уравнение такой цепи — линейное. Если в состав цепи входит хотя бы один нелинейный пассив ими или активный элемент, то она называется нелинейной, а процессы в ней описываются нелинейными дифференциальными уравнениями.

Параметры линейных идеализированных пассивных элементов и коэффициенты управления линейно управляемых источников могут либо иметь постоянные значения, либо изменяться во времени под действием некоторых факторов, непосредственно не связанных с токами или напряжениями этих элементов (например, емкость конденсатора может изменяться во времени вследствие изменения расстояния между обкладками; индуктивность катушки можно изменять путем перемещения сердечника). Идеализированные элементы первого типа называют линейными элементами с постоянными параметрами, элементы второго типа — линейными элементами с переменными параметрами. Параметрические изменение параметров происходит с частотой. линейным а м а элементы, у близкой к частоте токов или напряжений этих элементов, следует отличать от регулируемых элементов —конденсаторов переменной емкости, вариометров, подстроечных конденсаторов и др., у которых изменение параметров производится весьма медленно и только в процессе настройки или регулировки соответствующего устройства.

При составлении уравнений электрического равновесия параметрам регулируемых элементов приписывают некоторые фиксированные значения, а сами элементы относят к элементам с постоянными параметрами.

Цепи, составленные только из линейных элементов с постоянными параметрами, называются линейными цепями с постоянными параметрами или линейными инвариантными во времени цепями. Процессы в линейных инвариантных во времени цепях описываются линейными уравнениями с постоянными коэффициентами.

Линейные цепи, содержащие хотя бы один элемент с переменными параметрами, называются линейными параметрическими цепями. Процессы в линейных параметрических цепях описываются линейными уравнениями с переменными коэффициентами.

В общем случае дифференциальное уравнение линейной цепи с сосредоточенными параметрами имеет следующий вид:

где у — искомая реакция цепи (ток или напряжение какой-либо ветви); 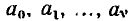— коэффициенты, определяемые параметрами пассивных элементов и коэффициентами управления управляемых источников. В дифференциальном уравнении линейной инвариантной во времени цепи эти коэффициенты постоянны, в дифференциальном уравнении линейной параметрической цепи, по крайней мере, один из них является функцией времени.

Правая часть уравнения (1.61) есть линейная комбинация функций, описывающих внешнее воздействие на цепь х (t), и их производных. При выключении всех источников она становится равной нулю.

Значение v характеризует порядок сложности цепи (порядок цепи) и равно числу реактивных элементов (емкостей и индуктивностей), энергетическое состояние которых может быть задано независимо (подробнее этот вопрос будет рассмотрен в гл. 6). Различают цепи нулевого порядка (не содержащие реактивных элементов), первого, второго и более высоких порядков.

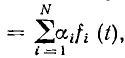
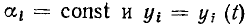
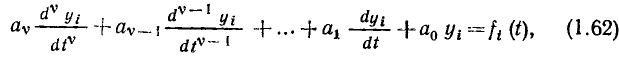
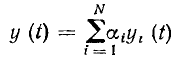
Для линейных уравнений вида (1.61) сформулирована теорема наложения (теорема суперпозиции). Если f(t) где являются решениями уравнений

то является решением уравнения (1.61).

Математически это значит, что решение линейного уравнения (1.61) со сложной правой частью можно выразить через решения уравнений (1.62) с более простой правой частью.

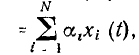
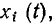
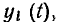
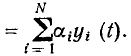
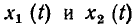
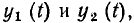
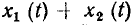
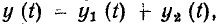
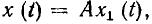
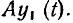
На теореме наложения базируется широко используемый в теории цепей принцип наложения (принцип суперпозиции): реакция у (t) линейной цепи на сложное воздействие х (t) представляющее собой линейную комбинацию более простых воздействий равна линейной комбинации реакций вызванных каждым из простых воздействий в отдельности, у (t) В частности, если внешним воздействиям соответствуют реакции то внешнему воздействию х (t) соответствует реакция а внешнему воздействию где А = const, реакция у(t) = Применение принципа наложения существенно облегчает исследование процессов в линейных электрических цепях, он лежит в основе многих широко используемых методов анализа.

Состояние теории цепей в значительной степени определяется степенью разработанности теории и методов решения соответствующих дифференциальных уравнений. К настоящему времени разработаны общие методы решения только линейных дифференциальных уравнений с постоянными коэффициентами, поэтому наиболее законченный вид имеет теория линейных инвариантных во времени цепей, которые в дальнейшем будем называть просто линейными цепями.

• Линейные цепи при гармоническом воздействии
• Нелинейные резистивные цепи
• Преобразование схем электрических цепей
• Установившиеся процессы в линейных электрических цепях
• Линии с распределенными параметрами
• Идеализированные пассивные элементы
• Идеализированные активные элементы
• Топологии электрических цепей

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.