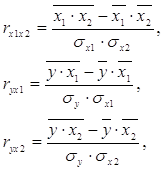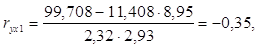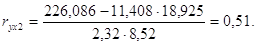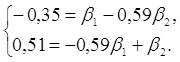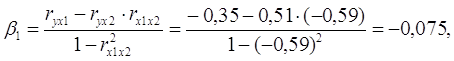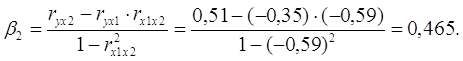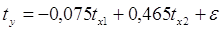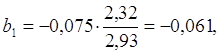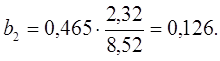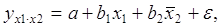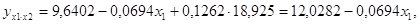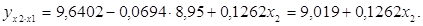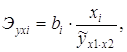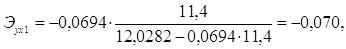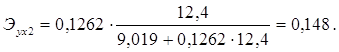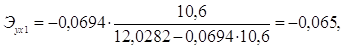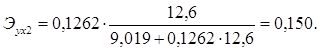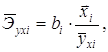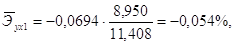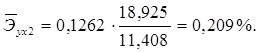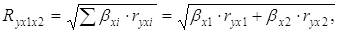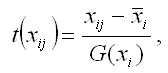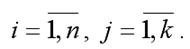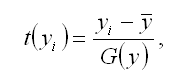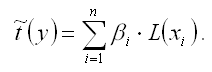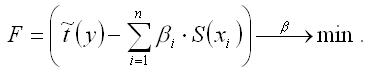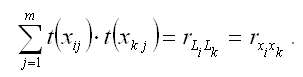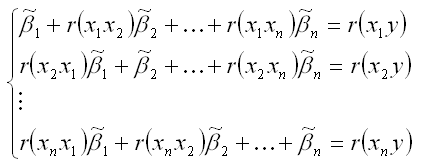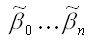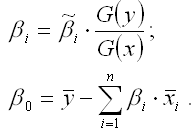Запишите уравнение регрессии в стандартизованной форме

Построение уравнения регрессии в стандартизованном масштабе

4.2 Построение уравнения регрессии в стандартизованном масштабе

Параметры множественной регрессии можно определить другим способом, когда на основе матрицы парных коэффициентов корреляции строится уравнение регрессии в стандартизованном масштабе:

,

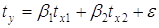
Применяя МНК к уравнению множественной регрессии в стандартизованном масштабе, после соответствующих преобразований получим систему нормальных уравнений вида:

где rух1, rух2 – парные коэффициенты корреляции.

Парные коэффициенты корреляции найдем по формулам:

Система уравнений имеет вид:

Решив систему методом определителей, получили формулы:

Уравнение в стандартизированном масштабе имеет вид:

Таким образом, с ростом уровня бедности на 1 сигму при неизменном среднедушевом доходе населения, общий коэффициент рождаемости уменьшится на 0,075 сигмы; а с увеличением среднедушевого дохода населения на 1 сигму при неизменном уровне бедности, общий коэффициент рождаемости возрастет на 0,465 сигмы.

Во множественной регрессии коэффициенты «чистой» регрессии bi связаны со стандартизованными коэффициентами регрессии βi следующим образом:

.

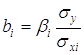
5. Частные уравнения регрессии

5.1 Построение частных уравнений регрессии

Частные уравнения регрессии связывают результативный признак с соответствующими факторами х при закреплении других учитываемых во множественной регрессии факторов на среднем уровне. Частные уравнения имеют вид:

.

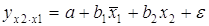
В отличие от парной регрессии частные уравнения регрессии характеризуют изолированное влияние фактора на результат, т.к. другие факторы закреплены на неизменном уровне.

В данной задаче частные уравнения имеют вид:

5.2 Определение частных коэффициентов эластичности

На основе частных уравнений регрессии можно определить частные коэффициенты эластичности для каждого региона по формуле:

Рассчитаем частные коэффициенты эластичности для Калининградской и Ленинградской областей.

Для Калининградской области х1=11,4, х2=12,4, тогда:

Для Ленинградской области х1 =10,6, х2=12,6:

Таким образом, в Калининградской области при увеличении уровня бедности на 1%, общий коэффициент рождаемости сократится на 0,07%, а при увеличении среднедушевых доходов на 1%, общий коэффициент рождаемости возрастет на 0,148%. В Ленинградской области при увеличении уровня бедности на 1%, общий коэффициент рождаемости сократится на 0,065%, а при увеличении среднедушевых доходов на 1%, общий коэффициент рождаемости возрастет на 0,15%.

5.3 Определение средних коэффициентов эластичности

Средние по совокупности показатели эластичности находим по формуле:

Для данной задачи они окажутся равными:

Таким образом, с ростом уровня бедности на 1%, общий коэффициент рождаемости в среднем по совокупности сократится на 0,054% при неизменном среднедушевом доходе. При увеличении среднедушевого дохода на 1%, общий коэффициент рождаемости в среднем по изучаемой совокупности возрастет на 0,209% при неизменном уровне бедности.

6. Множественная корреляция

6.1 Коэффициент множественной корреляции

Практическая значимость уравнения множественной регрессии оценивается с помощью показателя множественной корреляции и его квадрата – коэффициента детерминации. Показатель множественной корреляции характеризует тесноту связи рассматриваемого набора факторов с исследуемым признаком, т.е. оценивает тесноту связи совместного влияния факторов на результат.

Величина индекса множественной корреляции должна быть больше или равна максимальному парному индексу корреляции. При линейной зависимости признаков формула индекса корреляции может быть представлена следующим выражением:

Ryx1x2 =.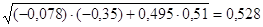

Таким образом, связь общего коэффициента рождаемости с уровнем бедности и среднедушевым доходом слабая.

Запишите уравнение регрессии в стандартизованной форме

Стандартизованное уравнение регрессии соответствует нормированным значениям переменной, переход к которым от исходных значений совершается го формуле [c.153]

Коэффициенты регрессии в (4.14) несопоставимы между собой, а / -коэффициенты уже сопоставимы. Поэтому для аналитика именно стандартизованное представление уравнения регрессии имеет особую значимость, поскольку позволяет дать сравнительную характеристику значимости факторов чем больше значение / -коэффициента, тем более существен фактор с позиции влияния его на результативный показатель. Бета-коэффициенты могут использоваться для установления нормативов, разработки весовых коэффициентов при конструировании различных сложных аналитических показателей (например, уровень научно-технического прогресса). [c.125]

Постройте уравнение регрессии в стандартизованном масштабе и сделайте выводы. [c.82]

Анализируя его, мы видим, что при той же занятости дополнительный рост стоимости основных производственных фондов на 1 тыс. руб. влечет за собой увеличение затрат в среднем на 1,2 тыс. руб., а увеличение численности занятых на одного человека способствует при той же технической оснащенности предприятий росту затрат в среднем на 1,1 тыс. руб. Однако это не означает, что фактор х оказывает более сильное влияние на издержки производства по сравнению с фактором х2. Такое сравнение возможно, если обратиться к уравнению регрессии в стандартизованном масштабе. Предположим, оно выглядит так [c.107]

Это позволяет от уравнения регрессии в стандартизованном масштабе [c.107]

Компьютерные программы построения уравнения множественной регрессии в зависимости от использованного в них алгоритма решения позволяют получить либо только уравнение регрессии для исходных данных, либо, кроме того, уравнение регрессии в стандартизованном масштабе. [c.108]

Рассчитанные по рекуррентной формуле частные коэффициенты корреляции изменяются в пределах от —1 до +1, а по формулам через множественные коэффициенты детерминации — от 0 до 1. Сравнение их друг с другом позволяет ранжировать факторы по тесноте их связи с результатом. Частные коэффициенты корреляции, подтверждая ранжировку факторов по их воздействию на результат, на основе стандартизованных коэффициентов регрессии /3-коэффициентов) в отличие от последних дают конкретную меру тесноты связи каждого фактора с результатом в чистом виде. Если из стандартизованного уравнения регрессии Л = Дч q + V 2 + з г з следует, что , > 2 > /3XJ, т. е. по силе влияния на результат порядок факторов таков Х , х2, х3, то этот же порядок факторов определяется и по соотношению частных коэффициентов корреляции, ГуХ] хт > г 2, Х ХЗ > г хт. [c.127]

Величины t показывают, на сколько среднеквадратических отклонений отстоит данная варианта от средней арифметической. Такое преобразование носит название стандартизации масштаба. Как следует из определения, величины t безразмерны. Подсчитаем коэффициенты для уравнения регрессии в стандартизованном масштабе [c.88]

Проиллюстрируем смысл р-коэффициентов на задаче анализа размеров улова рыбы. В соответствии с парными коэффициентами корреляции (табл. 77) получим уравнение регрессии в стандартизованном масштабе [c.129]

Но уравнения регрессии в стандартизованном и натуральном масштабах еще не позволяют решить две важные задачи. Очевидно, что для множественной регрессии, как и для парной, при любых коэффициентах регрессии разброс эмпирических точек вокруг поверхности регрессии может быть любым. Это приводит к тому, что во-первых, необходимо определить степень соответствия выбранного вида теоретической регрессии эмпирическому распределению или же (при фиксированном виде регрессии) определить уровень тесноты связи анализируемого показателя и группы изучаемых факторов. Поскольку же все факторы воздействуют на исследуемый показатель одновременно и мы не можем экспериментально отделить влияние одного фактора от влияния другого, возникает проблема, во-вторых, найти степень тесноты связи между изучаемым показателем и каждым фактором, предполагая, что все остальные заданы на постоянном уровне. [c.131]

С их помощью решим систему нормальных уравнений, чтобы определить коэффициенты уравнения регрессии в стандартизованном масштабе. [c.134]

Нетрудно видеть, что путем замены на 2 и дальнейших простых преобразований можно прийти к системе нормальных уравнений в стандартизованном масштабе. Подобное преобразование мы будем применять в дальнейшем, поскольку нормирование, с одной стороны, позволяет нам избежать слишком больших чисел и, с другой стороны, сама вычислительная схема при определении коэффициентов регрессии становится стандартной. [c.136]

Вид графа непосредственных связей говорит о том, что при построении уравнения регрессии только по двум факторам — количеству тралений и времени чистого траления— остаточная дисперсия ст .з4 не отличалась бы от остаточной дисперсии а .23456. полученной из уравнения регрессии, построенного по всем факторам. Чтобы оценить различие, мы обратимся в данном случае к выборочной оценке. 1.23456 = 0,907, а 1.34 = 0,877. Но если скорректировать коэффициенты по формуле (38), то 1.23456=0,867, a / i.34= = 0,864. Различие вряд ли можно считать существенным. Более того, г14 = 0,870. Это наводит на мысль, что количество тралений почти не оказывает непосредственного влияния на размер улова. Действительно, в стандартизованном масштабе 1.34 = 0,891 4 — 0,032 3- Нетрудно убедиться, что коэффициент регрессии при t3 недостоверен даже при очень низком доверительном интервале. [c.187]

Теснота парной линейной корреляционной связи, как и любой другой показатель, может быть измерена корреляционным отношением ц. Кроме того, при линейной форме уравнения применяется другой показатель тесноты связи — коэффициент корреляции г . Этот показатель представляет собой стандартизованный коэффициент регрессии, т. е. коэффициент, выраженный не в абсолютных единицах измерения признаков, а в долях среднего квадратического отклонения результативного признака [c.241]

Рх/. — соответствующий коэффициент уравнения множественной регрессии в стандартизованном масштабе. [c.122]

Необходимо а) найти множественный коэффициент детерминации и пояснить его смысл 6) найти уравнение множественной регрессии Y по Х и Xi, оценить значимость этого уравнения и его коэффициентов на уровне а=0,05 в) сравнить раздельное влияние на зависимую переменную каждой из объясняющих переменных, используя стандартизованные коэффициенты регрессии и коэффициенты эластичности г) найти 95%-ные доверительные интервалы для коэффициентов регрессии, а также для среднего и индивидуальных значений себестоимости 1 т литья в цехах, в которых выработка литья на одного работающего составляет 40 т, а брак литья — 5%. [c.107]

Разработку многофакторной модели начинаем с определения коэффициентов уравнения множественной регрессии между результатами и факторными признаками в стандартизованном масштабе. [c.178]

Коэффициенты множественной регрессии в стандартизованном масштабе находим из системы линейных уравнений [c.179]

Применение в практических целях уравнения множественной регрессии в стандартизованном масштабе затруднительно, поэтому уравнение множественной регрессии следует перевести в натуральный масштаб. Перевод коэффициентов множественной регрессии из стандартизованного масштаба в натуральный производится по формуле [c.180]

К уравнению множественной регрессии в стандартизованном масштабе применим МНК. Стандартизованные коэффициенты регрессии (Р-коэффициенты) определяются из следующей системы уравнений [c.50]

Построить уравнение множественной регрессии в стандартизованной и естественной форме рассчитать частные коэффициенты эластичности, сравнить их с Pj и р2 > пояснить различия между ними. [c.56]

Найдите уравнение множественной линейной регрессии в стандартизованном масштабе и сделайте выводы. [c.81]

Найдите уравнение множественной регрессии в стандартизованном и натуральном масштабе. [c.88]

В справедливости данной формулы можно убедиться, если обратиться к линейному уравнению множественной регрессии в стандартизованном масштабе и определить для него индекс множественной корреляции как [c.114]

Простейшим случаем является модель звена линейной причинной цепи, т. е. детерминации следствия у, всего лишь одной переменной — причиной х. Уравнение этой модели в форме линейной регрессии будет иметь вид (для стандартизованных переменных) [c.216]

Обозначим а через ух. В дальнейшем так будем обозначать коэффициенты уравнений линейной регрессии в стандартизованном масштабе. Следовательно, ty = р tx. В последнем уравнении коэффициент ух показывает, на сколько среднеквадратических отклонений изменится моделируемый признак -при изменении фактора (аргумента) на одно среднеквадратичное отклонение. Этот коэффициент для парной зависимости принято называть парным коэффи- [c.88]

Оценки коэффициентов регрессии для стандартизованных переменных получаются из решения системы уравнений [c.252]

Уравнение множественной прямолинейной регрессии в стандартизованном масштабе имеет вид [c.125]

Если записать уравнение чистой регрессии в стандартизованном масштабе, то тогда в уравнении множественной регрессии необходимо лишь исключить члены с закрепляемыми переменными [c.128]

Численность рабочих Р зависит от объема выполненных работ О, уровня механизации См и от объема применения сборных конструкций /Иж.б. В стандартизованном масштабе уравнение множественной регрессии запишется с учетом обозначений по аналогии с [88] в следующем виде [c.149]

Уравнение множественной регрессии Р от О, См, /Иж.6 в стандартизованном масштабе следующее [c.150]

Линейное уравнение множественной регрессии у от х и хг имеет вид у = а+Ь л 1+Й5Х2. Для расчета его параметров применим метод стандартизации переменных и построим искомое уравнение в стандартизованном масштабе ty = j tX + J2 x2 Расчет Р-коэффициентов выполним по формулам [c.57]

Интересно также выявить, как изменяется исследуемый показатель при изменении факторов, измеряемых в натуральных единицах. От уравнения регресии в стандартизованном масштабе к уравнению регрессии в натуральном масштабе можно перейти следующим образом. Пусть в ре зультате расчетов получено уравнение регрессии [c.130]

Согласованность частной корреляции и стандартизованных коэффициентов регрессии наиболее отчетливо видна из сопоставления их формул при двухфакгорном анализе. Для уравнения [c.127]

Расчет уравнения множественной регрессии начинается перевода всел переменных в единый масштаб — стандартизованный В качестве единицы измерения в этом масштабе принято среднее квадратическое отклонение а. [c.125]

Линейная модель множественной регрессии стандартизированного масштаба

Помимо классического метода наименьших квадратов для определения неизвестных параметров линейной модели множественной регрессии β₀…βm используется метод оценки данных параметров через β-коэффициенты (коэффициенты модели регрессии в стандартных масштабах).

Построение модели множественной регрессии в стандартизированном или нормированном масштабе означает, что все переменные, включенные в модель регрессии, стандартизируются с помощью специальных формул.

Посредством процесса стандартизации точкой отсчёта для каждой нормированной переменной устанавливается её среднее значение по выборочной совокупности. При этом в качестве единицы измерения стандартизированной переменной принимается её среднеквадратическое отклонение σ.

Факторная переменная х переводится в стандартизированный масштаб по формуле:

где x_ij – значение переменной xjв i-том наблюдении;

G(xj) – среднеквадратическое отклонение факторной переменной x_i;

Результативная переменная у переводится в стандартизированный масштаб по формуле:

где G(y) – среднеквадратическое отклонение результативной переменной у.

Если между исследуемыми переменными в исходном масштабе является линейной, то процесс стандартизации не нарушает этой связи, поэтому стандартизированные переменные будут связаны между собой линейно:

Неизвестные коэффициенты данной функции можно определить с помощью классического метода наименьших квадратов для линейной модели множественной регрессии. В этом случае минимизируется функционал F вида:

В результате минимизации данного функционала получим систему нормальных уравнений, переменными в которой будут являться парные коэффициенты корреляции между факторными и результативной переменной. Такой подход основывается на следующем равенстве:

Система нормальных уравнений для стандартизированной модели множественной регрессии имеет вид:

В связи с тем, что полученная система нормальных уравнений является квадратной (количество уравнений равняется количеству неизвестных переменных), то оценки коэффициентов

можно рассчитать с помощью метода Крамера, метода Гаусса или метода обратных матриц.

Рассчитанные из системы нормальных уравнений β-коэффициенты в стандартизированном масштабе необходимо перевести в масштаб исходных данных по формулам:

Рассмотрим метод Гаусса решения квадратных систем линейных уравнений. Суть данного метода заключается в том, что исходная квадратная система из n линейных уравнений с n неизвестными переменными преобразовывают к треугольному виду. Для этого в одном и уавнений системы оставляют все неизвестные переменные. В другом уравнении сокращают одну из неизвестных переменных для того, чтобы число неизвестных стало (n-1). В следующем уравнении сокращают две неизвестных переменных, чтобы число переменных стало (n-2). В результате данных преобразований исходная система уравнений примет треугольный вид, первое уравнение которой содержит все неизвестные, а последнее – только одну. В последнем уравнении системы остаётся (n-(n-1)) неизвестных переменных, т. е. одна неизвестная переменная, которая называется базисной. Дальнейшее решение сводится к выражению свободных (n-1) неизвестных переменных через базисную переменную и получению общего решения квадратной системы линейных уравнений.