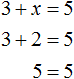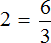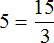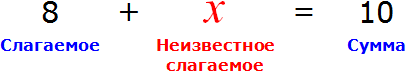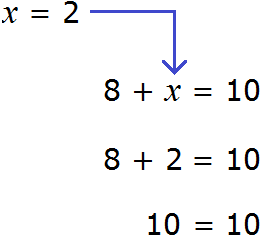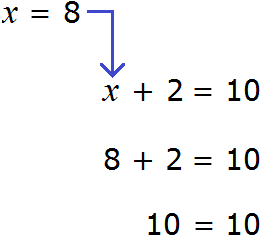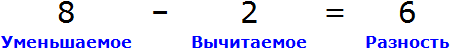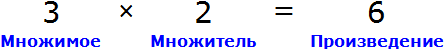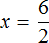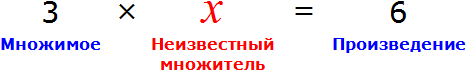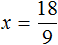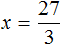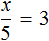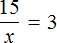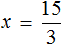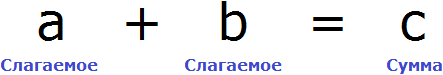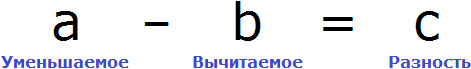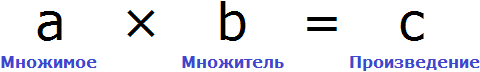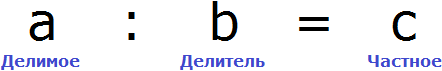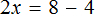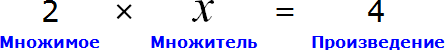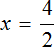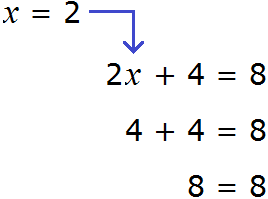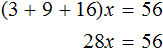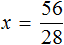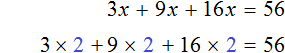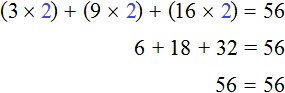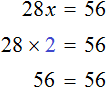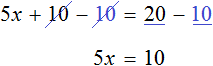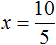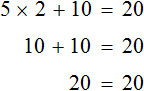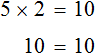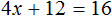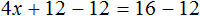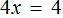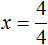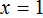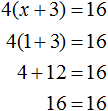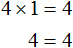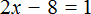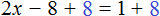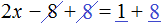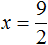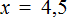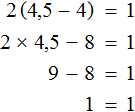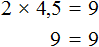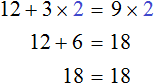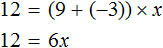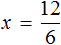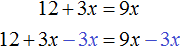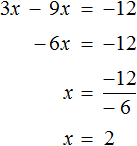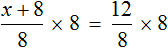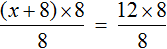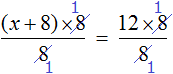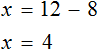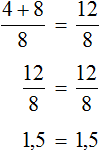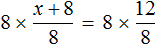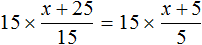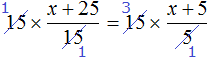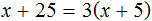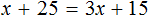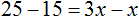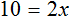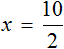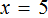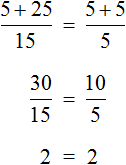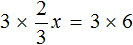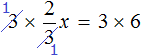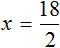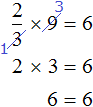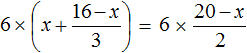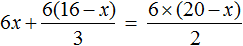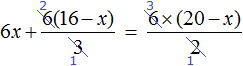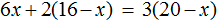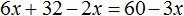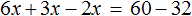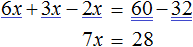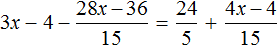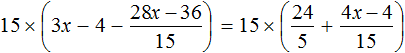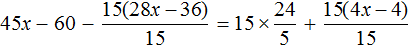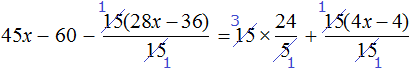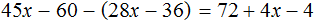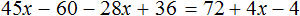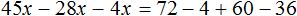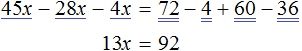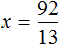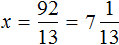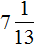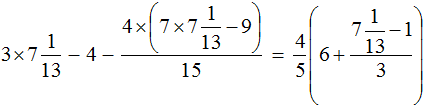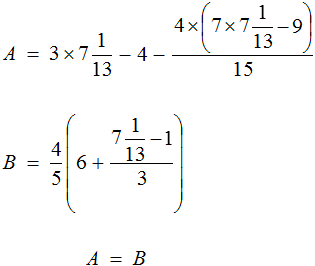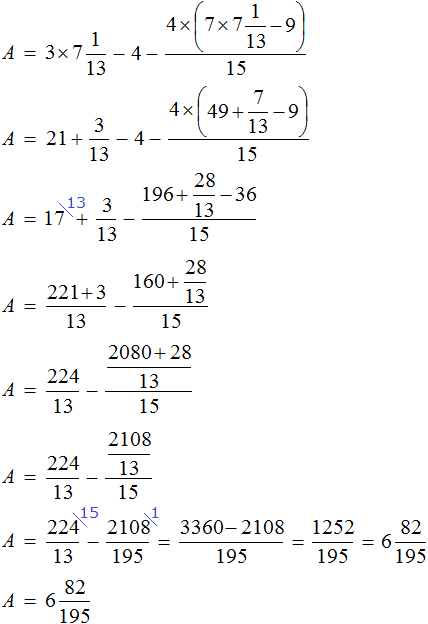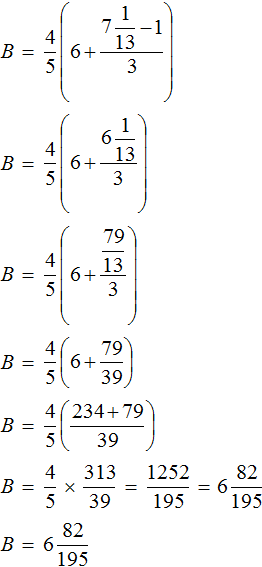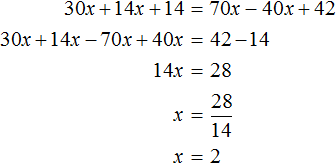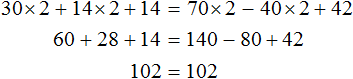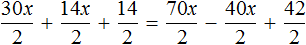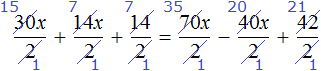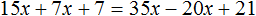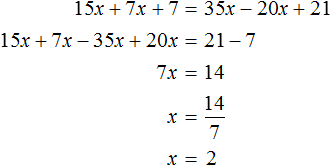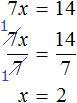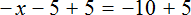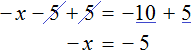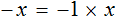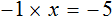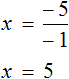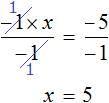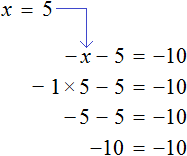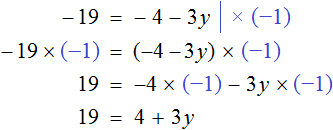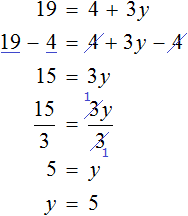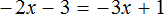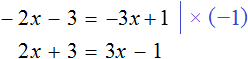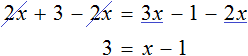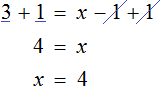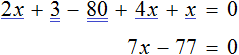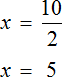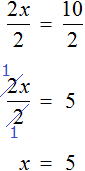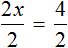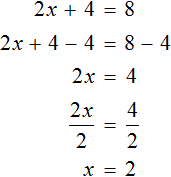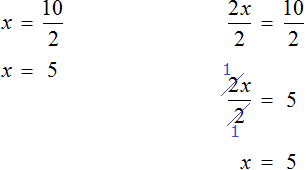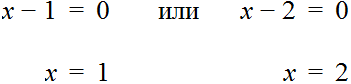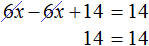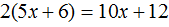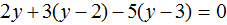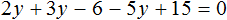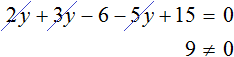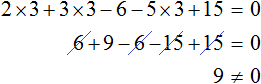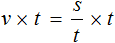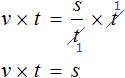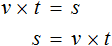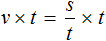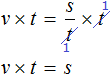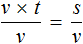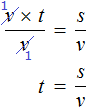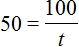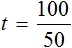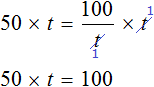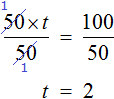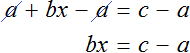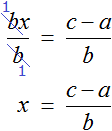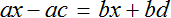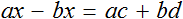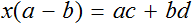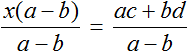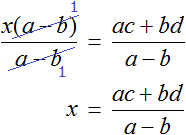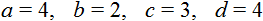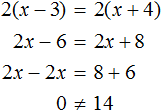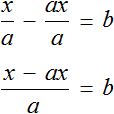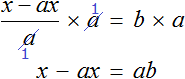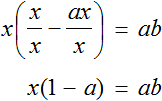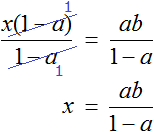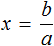Тема урока: «Решение линейных уравнений, содержащих формулы сокращенного умножения»
Разделы: Математика
Цели урока:
- Обработка рациональных приёмов решения уравнений.
- Выработка умения решения задач.
- Развитие элементов творческой деятельности учащихся и умения контролировать свои действия.
- Повторение решения уравнений.
Оборудование: печатные бланки, таблица.
Тип урока: урок- семинар комплексного применения знаний, умений и навыков.
1.Организационный момент. Сообщается план семинара.
2.Сообщение по теме « Уравнение»
3. Решение линейных уравнений.
4.Сообщение о формулах сокращённого умножения.
(Работа у доски и по карточкам.)
а) Решение уравнений, содержащих квадрат суммы.
б) Решение уравнений, содержащих квадрат разности.
в) Решение квадратных уравнений, содержащих разность квадрата.
г) Решение уравнений, содержащих несколько формул.
5. Решение задачи.
6. Творческая работа учащихся.
7. Подведение итогов урока.
Ход урока.
1.Вступительное слово учителя.
Один начинающий волшебник, герой шуточной песенки, неумело обращался с заклинаниями, в результате вместо грозы у него получилась коза, а вместо утюга слон. Чтобы решить уравнение, тоже нужно совершить ряд превращений (алгебраических преобразований) и делать их нужно очень осмотрительно. Сегодня мы ещё раз увидим, какая удивительная сила заключена в формулах сокращённого умножения и как ловко они работают при решении уравнений.
Прежде всего, нужно чётко понимать, чем вы занимаетесь, когда решаете уравнение. Что, значит, решить уравнение и нужно знать, что главная задача при решении любого уравнения — свести его к простейшему.
И сегодня нам будут помогать формулы Сокращённого умножения.
2. Сообщение по теме «Уравнение»
3. Решение линейных уравнений у доски (учащиеся класса записывают решения в тетрадях)
| а) 2-3(x+2)=5-2x; 2-3x-6=5-2x, -3x+2x=5-2+6 -x =9 x=-9 Ответ:-9. | б) 20+4(2x-5)=14x+12 20+8x-20=14x+12, 8x-14x=12, -6x=12, x=-2, Ответ: -2. |
Решение уравнений по карточкам.
в) 4(2-3x)+7(6x+1)-9(9x+4)=30
г) 3-5(x+1)=6-4x.
Сообщение №2.
Слово о формулах.
4. Решение уравнений, содержащих квадрат суммы и квадрат разности.
а) x+(5x+2)2 =25(1+x2).
б) (x-6)2-x(x+8)=2.
Решение уравнений по карточкам.
в) (2-x)2-x(x+1,5)=4
г) x(x-1)-(x-5)2=2.
5. Решение уравнений, в которых содержится формула разности квадратов.
Работа у доски.
8x(1+2x)-(4x+3)(4x-3)=2x.
8x+16×2-(16×2-9)=2x,
8x+16×2-(16×2-9)=2x,
8x+16×2-16×2+9=2x,
8x-2x=-9,
6x=-9,
x=-1,5
Ответ: -1,5
Решение задачи.
Сторона первого квадрата на 2см. больше стороны второго, а площадь первого на 12 см больше площади второго. Найдите периметры этих квадратов.
Пусть x см сторона второго квадрата. Тогда(x+2) см сторона первого квадрата. Площадь первого (x+2) 2 см 2 ,а площадь второго x 2 .
Составляем уравнение:
(x+2) 2 -x 2 =12
x 2 +4x+4-x 2 =12,
4x=12-8,
4x=8,
x=2.
Если x=2,то 4x=4*2=8
Если x=2, то 4(x+2)=4(2+2)=16.
Ответ:16см,8см.
6. Решение разных уравнений, содержащих формулы сокращённого умножения.
7.Творческая работа учащихся. Заполнение таблицы.
Узнайте фамилию величайшего математика XVII века. Для этого зачеркните
буквы, не связанные с найденными ответами.
(Декарт)
| -9 | 8,2 | -2 | 3,4 | 1 | 3,1 | 1,7 | 15 | -1,5 | 17 | 11 | 3 |
| Д | П | Е | Ф | К | С | А | И | Р | Г | Ш | Т |
Приложение к уроку.
Решение линейных уравнений.
| 4(2-3x)+7(6x+1)-9(9x+4)=30 8-12x+42x+7-81-36=30, 51x-21=30, 51x=51 x=1 Ответ: 1. | 3-5(x+1)=6-4x, 3-5x-5=6-4x, -5x+4x=6-3+5, -x=8x= -8. Ответ:-8. |
Решение уравнений, содержащих квадрат суммы и квадрат разности.
| x+(5x+2) 2 =25(1+x 2 ) x+(25x 2 +20+4)=25(1+x 2 ) x+25x 2 +20x+4=25+25x 2 , 21x+25x 2 -25x 2 =25-4, 21x=21 x=1 Ответ:1. | (x -6) 2 -x(x+8)=2 x 2 -12x+36-x 2 -8x=2 -20x=2-36, -20x=-34, x=1,7 Ответ: 1,7. |
Работа по карточкам.
| (2-x)2-x(x+1,5)=4, 4-4x+x 2 -x 2 -1,5x=4, -4x-1,5x=4-4, -5,5 x=0 Ответ:0. | x(x-1)-(x-5) 2 =2 x 2 -x-(x 2 -10x+25)=2, x 2 -x-x 2 +10x-25=2 9x=27 x=3 Ответ: 3. |
Решение разных уравнений содержащих несколько формул сокращённого умножения.
| (x-4x)+(x+4)+(3x-4)(x+2)=(2x+3) 2 x 2 -16+3x 2 +6x-4x-8=4x 2 +12x+9 -10x=33 x=-3,3 Ответ:3,3. | ( 2x+3)2-4(x-1)(x+1)=49 4x 2 +12x+9-4(x 2 -1)=49 4x 2 +12x+9-4x 2 +4=49 12x+13=49 12x=36 X=3 Ответ: 3. |
8. Подведение итогов урока.
Оформление формул — требования и примеры в диссертации
Диссертации по техническим специальностям – это сложные научно-исследовательские работы, состоящие из множества формул, уравнений, графиков и других наглядных пособий. Требования к оформлению этих элементов строго регламентируются ГОСТом.
Основные правила оформления формул в диссертации
- Оформление формул в кандидатских диссертациях основано на соответствующих технико-орфографических правилах.
- Если формула, использованная в тексте диссертации, пронумерована или громоздкая (наличие интегрирования, дифференцирования, произведения/суммы), ее рекомендуется размещать на нескольких строчках. Переносится уравнение после знаков «=» или умножение/деление/плюс/минус («х», «:», «+», «-»)
Чтобы сэкономить место на листе, однотипные формулы, удаленные от текста научной работы, подаются в одной строчке. В некоторых случаях, они вписываются в строку текста (правило актуально для несложных и небольших формул).
Примечание. Значения коэффициентов и использованных символов размещаются с новой строки. Формат первой строки пояснения – слово «где» (без использования двоеточия). Обязательной нумерации подлежат уравнения со ссылками в тексте диссертации.
Особенности нумерации
Для порядковой нумерации формул используют арабские цифры. Они размещаются в круглых скобках и располагаются в правой части листа без точек возле конца формулы. Если номер не поместился в конце строки, разрешается указать его чуть ниже, на уровне следующей строки.
Правило нумерации для формул в рамке следующее – цифра записывается за пределами рамки с правой части уравнения напротив основной его строки. Формулы-дроби нумеруются напротив уровня их основной горизонтальной черты.
Пунктуация и формулы в диссертации
При составлении предложений, соискателю ученой степени следует учесть, что формулы являются их равноправным элементом. Перед уравнениями и после них соблюдаются все правила пунктуации.
Обратите внимание! Двоеточие перед формулой используется в двух случаях – наличие обобщающего слова в тексте или особенность построения предложения перед уравнением. Допускается не ставить знаки препинания после определителей и матриц (причина – громоздкость уравнений).
Оформление формул по ГОСТу в диссертации
Основные требования к формулам, регламентируемые положениями ГОСТ.
- Пояснения к составляющим уравнения (символы, числовые коэффициенты) указываются в тексте или сразу после формулы.
- Перенос формулы на другую строку – исключительно с переносом знака операции с его повтором в начале следующей строки.
- Для рукописных вариантов диссертаций, формулы указываются чертежным или машинописным шрифтом. Рекомендуемая высота – до 2,5 мм. Запрещается использовать сочетание рукописных и машинописных составляющих в одной формуле.
- Использование сквозной нумерации для всех формул, кроме размещенных в приложении. Единственная формула подлежит обязательной нумерации (пример – (1)).
- Ссылки на формулы указываются в круглых скобках.
- Формулы в приложении диссертации нумеруются отдельно, арабскими цифрами с добавлением символа, характеризующего приложение. (например, формула С.2).
Компания «Диссертация» оказывает услуги по написанию сложных технических документов, диссертаций, курсовых работ и дипломных проектов. Каждая работа проходит обязательную многоуровневую проверку на соответствие требованиям ВАК и ГОСТ. Мы гарантируем конфиденциальность каждому клиенту и предлагаем удобную форму оплаты за заказ. Будем рады видеть вас в числе наших заказчиков!
Оформление формул в ворде по госту
- Оформление формул в кандидатских диссертациях основано на соответствующих технико-орфографических правилах.
- Если формула, использованная в тексте диссертации, пронумерована или громоздкая (наличие интегрирования, дифференцирования, произведения/суммы), ее рекомендуется размещать на нескольких строчках. Переносится уравнение после знаков «=» или умножение/деление/плюс/минус («х», «:», « », «-»)
Чтобы сэкономить место на листе, однотипные формулы, удаленные от текста научной работы, подаются в одной строчке. В некоторых случаях, они вписываются в строку текста (правило актуально для несложных и небольших формул).
При написании формул используются только общепринятые символы, если они заменяются другими знаками, это обязательно указывается в перечне сокращений и условных обозначений.
- Все формулы в дипломной работе пишутся в отдельной строке.
- Расстояние между формулой и окружающим ее верхним и нижним текстом – минимум один интервал.
- Длинные формулы переносятся на нижнюю строчку, при этом разрыв можно делать только на математических знаках, повторяя их в начале следующей строки.
Разрыв предпочтительнее делать в месте расположения знака равенства.
При переносе по знаку умножения обозначения делаются только символом «х», ни в коем случае не точкой.
- Если необходимо сделать разрыв при наличии в формуле дробных величин с длинными знаменателями или числителями их надо условно обозначить коротким символом, который сразу же расшифровать ниже.
- При переносе формул желательно располагать их не с выравниванием по центру, как обычно, а со сдвигом: первую строку – влево, вторую – вправо.
- Делается это для того, чтобы «уравновесить» страницу и облегчить восприятие математического равенства.
- Расшифровка символов и коэффициентов (экспликация) делается сразу за формулой, после которой ставится запятая, а ниже, на следующей строке, без абзацных отступов пишутся слово «где» (двоеточие за ним не ставится) и последующие разъяснения.
Символы поясняются в порядке, соответствующем их месту в формуле. Для дробей сначала дается экспликация числителя, затем – знаменателя. Вместе с расшифровкой можно приводить и единицы измерения.
Как правило, значение каждого символа указывается с новой строки, но в целях экономии места допускается давать пояснения обычным линейным текстом.
- В тексте дипломной работы отсылки к формулам делаются исключительно в круглых скобках: например, «Расчет прибыли производился по формуле (6)».
Если в строчке текста диплома последовательно расположены формулы, одна из которых заканчивается цифрой, а другая – начинается, то их разделяют точкой с запятой (;).
Этот же знак используют и для того, чтобы разграничить написанные друг за другом одно- и многострочные равенства.
А вообще, в сопровождающем формулы тексте применяется стандартная пунктуация, то есть математические выражения или отдельные символы считаются обычными членами предложения, поэтому знаки препинания в речевых конструкциях с ними ставятся по всем правилам русского языка.
Предлагаем ознакомиться: Срок оформления наследства после подачи заявления
- Если формул в тексте дипломной работы несколько, то они нумеруются, но не все, а только наиболее важные – те, на которые в дальнейшем делаются ссылки.
- Для нумерации формул в дипломной работе используются только арабские цифры, которые берутся в круглые скобки и проставляются в крайней позиции строки, на которой записано математическое выражение.
- Если формула длинная и переносится на следующую строку, то номер ставится на том уровне, где окончилась запись.
Нумерация формул в дипломе сквозная, то есть общая для всех глав работы, но возможен и вариант, когда порядковые номера присваиваются в пределах каждого раздела. В таких случаях для обозначения используется двойной индекс, в котором на первом месте указывается номер раздела, на втором через точку – самой формулы в нем.
В приложении к дипломной работе формулы нумеруются отдельно – в рамках каждого приложения с указанием на первой позиции его буквенного обозначения, на второй – номера формулы в нем.
Когда формулы образуют цельную группу, ей присваивается один общий номер. Если каждое равенство записывается отдельной строкой, то весь кластер объединяется фигурной скобкой.
Разновидностям основной, уже имеющей цифровое обозначение формулы можно давать те же номера, что уже присвоены базовому математическому выражению, но с буквенными индексами (алфавит – русский).
Промежуточные формулы, которые приводятся в тексте только для демонстрации этапов расчетов, можно обозначать русскими буквами или звездочками (оба варианта заключаются в круглые скобки): (д), (ж), (*), (****).
Нумерация листов
Все страницы текстового документа должны быть пронумерованы в обязательном порядке. Нумерации подлежит и титульный лист, но сам номер на нем не ставится. Номер по порядку должен находиться посередине нижней части страницы без точки.
Пронумерованными должны быть картинки и рисунки. Нумерация осуществляется посредством цифр. Как правило, рисунки центрируют по горизонтали. Пропускается одна строка перед и после рисунков. При маленьком размере рисунка разрешено его нахождение справа от текста. При этом отступ от основного текста должен составлять 0,5 сантиметра.
Для порядковой нумерации формул используют арабские цифры. Они размещаются в круглых скобках и располагаются в правой части листа без точек возле конца формулы. Если номер не поместился в конце строки, разрешается указать его чуть ниже, на уровне следующей строки.
Правило нумерации для формул в рамке следующее – цифра записывается за пределами рамки с правой части уравнения напротив основной его строки. Формулы-дроби нумеруются напротив уровня их основной горизонтальной черты.
Шрифт текста и параметры страницы
Для текстовой документации предусмотрены шрифты по ГОСТу для word. Отступать от норм недопустимо.
- Times New Roman, размер не меньше 12;
- Verdana, размеры 12 и 13;
- Calibri, размер 12;
- Arial, размеры 12 и 13;
Перед началом работы нужно выставить параметры страницы по ГОСТу в Ворде.
- Поля в ворде по ГОСТу;
- Красная строка (абзац);
- Размер бумаги;
- Ориентация «Альбомная»;
- Разметки.
ГОСТы и ЕСКД допускают оформление формул в дипломе двумя способами:
- От руки черными чернилами.
- На компьютере.
Чтобы заручиться поддержкой машинного интеллекта, особо сложного программного обеспечения не понадобится – хватит и возможностей обычного Microsoft Office. В версии 2010 года для перехода к работе с формулами надо кликнуть на «Вставку» в левом верхнем углу меню инструментов.
- Откроется вкладка с дополнительными опциями, в правом углу которой расположен блок для формул.
- Если щелкнуть на нее, откроется библиотека стандартных математических символов и уравнений и конструктор для построения собственных формул (рабочий шрифт по умолчанию – Cambria Math).
- Выбирать есть из чего.
Более подробные пошаговые инструкции, как создавать формулы в дипломе с помощью Ворд, есть на официальном сайте технической поддержки пользователей продуктов Microsoft.
Решая, как будете оформлять формулы в дипломе, выбирайте только один способ: или все уравнения вписываются от руки, или все печатаются на компьютере – винегрет не приветствуется ни ГОСТом, ни тем более вузовскими нормоконтролерами.
Пунктуация и формулы в диссертации
При составлении предложений, соискателю ученой степени следует учесть, что формулы являются их равноправным элементом. Перед уравнениями и после них соблюдаются все правила пунктуации.
Оформление формул по ГОСТу в диссертации
Основные требования к формулам, регламентируемые положениями ГОСТ.
- Пояснения к составляющим уравнения (символы, числовые коэффициенты) указываются в тексте или сразу после формулы.
- Перенос формулы на другую строку – исключительно с переносом знака операции с его повтором в начале следующей строки.
- Для рукописных вариантов диссертаций, формулы указываются чертежным или машинописным шрифтом. Рекомендуемая высота – до 2,5 мм. Запрещается использовать сочетание рукописных и машинописных составляющих в одной формуле.
- Использование сквозной нумерации для всех формул, кроме размещенных в приложении. Единственная формула подлежит обязательной нумерации (пример – (1)).
- Ссылки на формулы указываются в круглых скобках.
- Формулы в приложении диссертации нумеруются отдельно, арабскими цифрами с добавлением символа, характеризующего приложение. (например, формула С.2).
Компания «Диссертация» оказывает услуги по написанию сложных технических документов, диссертаций, курсовых работ и дипломных проектов. Каждая работа проходит обязательную многоуровневую проверку на соответствие требованиям ВАК и ГОСТ. Мы гарантируем конфиденциальность каждому клиенту и предлагаем удобную форму оплаты за заказ. Будем рады видеть вас в числе наших заказчиков!
Необходимо рассмотреть параметры, какие используют при составлении того или иного документа, согласно ГОСТу по оформлению документов.
Относительно большинства предпринимательских документов ограничения в оформлении отсутствуют. Официальная или техдокументация должны соответствовать критериям ГОСТа.
При составлении служебной документации шрифт используется по ГОСТу не для основного документооборота. Тем не менее, следует учитывать определенные моменты, которые указаны в локальных актах организации.
Определенные нормы при составлении служебных документов отсутствуют. ГОСТом предусмотрены параметры, максимально подходящие и допустимые в отношении всех символов.
В отношении параметра шрифта в документе указаны нормы предпочтительного характера (12 или 14). От выбранного варианта документа зависит шрифт. Допустимы и разновидности, близкие к указанным параметрам. При выборе опираться надо на читабельность текста, восприятие информации как с экрана, так и с листа, а также используемый формат бланка (А4, А5, А2).
При составлении государственной технической документации необходимо учитывать следующие действующие нормативно-правовые акты: ГОСТ 2 .105—95 и 7.32—2001. В указанных нормативах прописаны общие условия по отношению к формированию техдокументации.
Указания по поводу шрифта и размеров в таблицах не предусмотрены. Определяется только стиль и размер самой таблицы. Нумеруется она в рамках всего документа арабскими цифрами. Под таблицей обязательно указывается ее наименование. Располагается она под ссылкой в тексте. С заглавных букв начинаются заголовки столбцов и граф. Не допускается использовать кавычки при замене повторяющихся слов.
В таблице категорически запрещена графа, именуемая «Номер по порядку». Таблицу делят на части в том случае, когда графы и строки выходят за формат страницы. Слово «Таблица» упоминается один раз в левой части таблицы, над остальными частями помечают надписью «Продолжение таблицы» с указанием ее обозначения. Чертежи оформляются согласно ГОСТ 2 .304—81.
Если в документах встречаются формулы, то записывать их следует в центре листа. В роли символов используют обозначения, установленные государственными стандартами. В том случае, когда в главном тексте нет объяснений символов и числовых коэффициентов, из которых состоит формула, то эти данные описываются под самой формулой.
Оформление заголовка и подзаголовка
Все заголовки должны быть расположены в середине строки. Заголовки разделяют тройным интервалом сверху и снизу. ГОСТом рекомендовано каждую главу (раздел) начинать со следующей страницы. Также должны соблюдаться следующие условия:
- Нумерование цифрами каждого раздела и подраздела по всему основному документу.
- Разделы и подразделы всегда должны именоваться: недопустимо оставлять пустые строки.
- Обозначаются подзаголовки таким образом: нумеруется заголовок по порядку, затем через точку пишется номер по порядку подзаголовка (после номера заголовка и подзаголовка точки не ставятся).
- Подразделы и разделы начинаются с абзаца и с большой буквы (в конце точка не ставится).
- Если раздел состоит из двух предложений, то между ними обязательно ставится точка.
- Запрещено переносить слова.
- Введение и заключение нумерации не подлежат.
Оформление формул в дипломе
Формулы встречаются в дипломах не только студентов технических вузов, но и экономических и, иногда, гуманитарных. О том, что диплом должен быть оформлен должным образом вне зависимости от тематики, не нужно объяснять ни одному студенту.
К тому же, с оформлением многих элементов студенты знакомы еще по курсовым работам. Но, учитывая, что при написании курсовых работ преподаватели не так уж строго следят за оформлением работ, у многих студентов на этапе написания дипломного проекта вызывают немало вопросов такие элементы, как формулы.
Оформление формул в дипломе по ГОСТу
Как и весь диплом, оформление формул осуществляется по ГОСТ 7.32-2001. Этот ГОСТ описывает основные требования к написанию формулы, оформлению поясняющего текста и других ключевых моментов.
Так формула обычно пишется либо в центре строки, либо по левому краю с небольшим отступом. Размер шрифта символов в формуле может быть незначительно больше основного шрифта, используемого в тексте дипломного проекта. А перед формулой и после нее должны быть небольшие отступы, соответствующие одной пустой строке.
В том случае, если в дипломном проекте приводится сложная формула, длина которой превышает длину строки, разрешается перенос части формулы на следующую строчку. При этом перенос можно начинать после любого, обозначающего действие, математического знака.
Это может быть знак деления, сложения, равенства или некоторые другие знаки.
Важно помнить, что в месте переноса это знак дублируется, то есть знак ставится не только в конце строчки, на которой формула не поместилась, но и в начале следующей строки, куда формула переносится.
Пример оформления формул в дипломе
Под каждой формулой должен размещаться поясняющий текст, цель которого – кратко описать использованные в формуле обозначения и коэффициенты. Причем описываться должны все элементы формулы в порядке их употребления. Например, для второго закона Ньютона описание формулы будет выглядеть следующим образом:
- F=m∙a
- F – значение приложенной к телу силы,
- m – значение массы тела, к которому была приложена сила F,
- a – значение ускорения тела.
Конечно же, все эти элементы формулы можно расписать и гораздо подробнее в условиях решаемой задачи. Но делать этого не стоит – чаще всего таких формул в дипломном проекте несколько десятков, поэтому подробное описание формул может занять слишком большую часть дипломной работы.
Что вызовет сомнения преподавателей по поводу содержания работы – возможно требуемый объем дипломного проекта набирался с помощью аналогичных подробных описаний.
Описания формул должны быть краткими и в то же время достаточными, чтобы читающий диплом преподаватель мог понять, о чем идет речь и о том, как и откуда были взяты те или иные данные.
Для удобства все формулы должны нумероваться. Тогда студенту не обязательно в случае необходимости писать ранее упомянутую формулу еще раз, достаточно сделать ссылку на ранее описанную формулу. Особенно это актуально для дипломов технических тематик, в которых довольно часто приходится выводить нужный результат, используя несколько различных формул.
ГОСТ предусматривает несколько различных способов нумерации формул. Самый простой, но наименее удобный, способ – это сквозная нумерация. В этом случае формулы нумеруются по порядку арабскими буквами. Номер формулы указывается в той же строке, где размещается формула через некоторый промежуток. Номер формулы указывается в круглых скобках.
- На примере того же закона Ньютона оформление формулы при помощи сквозной нумерации будет выглядеть следующим образом:
- F=m∙a (1),
- Что будет означать, что указанная формула – первая в дипломном проекте.
Также допускается включать в нумерацию номер раздела или пункта, в котором формула размещается. Это более удобный способ, так как в этом случае найти формулу в тексте диплома гораздо проще, достаточно лишь знать раздел, в котором она находится.
При такой нумерации сначала указывается номер раздела, через точку от него пишется порядковый номер формулы в этом разделе. Если раздел состоит из нескольких пунктов, добавляется еще номер пункта.
Так, если формула второго закона Ньютона располагается в третьем пункте второго раздела, а в третьем пункте это уже седьмая по счету формула, то обозначить нумерацию следует таким образом:
Аналогичным образом нумеруются формулы и в приложении. Единственное различие – вместо номера раздела указывается обозначение приложения. Так как приложения обозначаются заглавными буквами русского алфавита, то нумерация формул вместо номера раздела будет содержать буквенное обозначение приложение. Это единственный случай нумерации формул, когда допускается использование букв.
Также ГОСТ допускает написание формул от руки с использование черных чернил. Особенно это актуально для сложных технических дипломов, в которых используются многоуровневые формулы.
Оформление диплома по ГОСТу (правила и требования)
Студенты выпускных курсов сталкиваются с вопросом, как оформить дипломную работу по ГОСТу. Проблема исходит от непонимания того, как правильно оформить диплом по государственному стандарту, что конкретно нужно делать. На кафедрах выдают методичку по оформлению выпускных квалификационных работ, но не все студенты ими пользуются.
В статье дается пошаговый алгоритм написания и оформления ВКР в соответствии с ГОСТ и пример дипломной работы.
Основные требования ГОСТа к оформлению дипломной работы
Оформление диплома по ГОСту – это основное требование, предъявляемое к выпускнику ВУЗа. Выпускная квалификационная работа представляет собой особую форму научного произведения.
Текст диплома состоит из шести этапов:
- Обоснование актуальности.
- Постановка целей и задач.
- Купить дипломную работуОпределение предмета и объекта исследования.
- Определение методов исследования.
- Описание процесса экспериментов или внедрения.
- Формулирование выводов и результатов.
Нумерация страниц начинается с введения.
Рамка диплома является обязательной, а потому стоит заранее оформить поля документа в соответствии:
- верхнее – 2 см.;
- нижнее – 2 см.;
- левое – 3 см.;
- правое – 1 см.;
- межстрочный интервал 1,5 пт.;
- выделение красной строки 1,25 см.
Выбор шрифта для диплома
Текст дипломной работы печатается шрифтом Times New Roman:
- печать ведется на одной стороне формата бумаги А-4;
- все абзацы выделяются 14 размером строчным регистром;
- в таблицах используется 12 кегль строчного регистра;
Однако такой стандарт не распространяется на приложения. Заполнение чертежной таблицы и сама подпись чертежей в электронном документе оформляется типом А, его нет в стандартном наборе Office.
Оформления титульного листа
Пример титульного листа на каждой кафедре есть в методическом пособии. Образец выполнен в соответствии с требованиями к оформлению диплома:
- 14 кеглем TMR посреди строки прописным регистром пишется наименование ведомства, к которому относится учебное заведение;
- ниже название ВУЗа;
- на следующей строке указывается кафедра;
- далее прописным регистром и полужирным выделением посередине прописывается словосочетание «ДИПЛОМНАЯ РАБОТА»;
- на следующей строке, оставив полужирное выделение, но изменив кегль на 16 и установив строчной регистр, пишется название труда;
- 14 кеглем по правому краю, в некоторых университетах требуют выставить красную строку на 8, заполняются данные об авторе работы;
- ниже идет запись о научном руководителе;
- в некоторых учебных заведениях ниже вносятся данные о заведующем кафедрой с пометкой «допущен к защите», но не всегда;
- также может быть строчка «дипломная работа защищена»;
- внизу страницы посередине указывается город и год защиты, в зависимости от учебного заведения есть вариации:
Правила оформления содержания (оглавления) диплома
диплома должно быть выдержано в определенных параметрах:
- отступ обозначения красной строки здесь не выделяется;
- Стоимость дипломной работы само слово «содержание» прописывается Times New Roman, кегль 16.
Ниже списком приводится вся структура работы:
- введение;
- первая часть работы;
- первый параграф первой части;
- второй параграф первой части;
- вторая часть работы;
- первый параграф второй части;
- второй параграф второй части;
- заключение;
- список использованных источников;
- приложение (если есть).
Для увеличения читабельности текста эта структура записывается в скрытую таблицу, проставляются точки до конца строки и во второй колонке таблицы вписывается номер страницы.
Как оформить ссылки (сноски) в пояснительной записке диплома
Приведение ссылок и сносок не менее важно. Так как все студенты в написании своих работ ссылаются на ту или иную информацию.
Все ссылки дипломных работ оформляются в квадратных скобках с указанием номера источника в том порядке, в котором он указан в списке литературы.
Правильное оформление цитирования в тексте диплома
Для получения более оригинальной работы следует некоторые теории и определения записывать в виде цитат:
- написать введение перед цитатой (автор теории заявляет: «цитата»);
- цитата заключается в кавычки («цитата»);
- в квадратных скобках указывается номер источника из списка литературы с обозначением страницы, из которой производилось цитирование ([3, стр. 125]).
Оформление формул и уравнений в дипломе
Формулы и уравнения в работах также необходимо вносить в диплом по ГОСТу:
- они выделяются в отдельную строку;
- слишком длинные формулы и уравнения переносятся после знаков: равенства, умножения или деления, сложения или вычитания. После переноса на новую строку знак дублируется;
- под формулой прописываются пояснения к ней;
- номера формул указываются арабскими цифрами по порядку в круглых скобках.
Оформление рисунков в дипломной работе
Единому оформлению подлежат все изображения графического материала, которые приводятся в работе:
На все графические сведения дается ссылка. Располагаются такие изображения после текста, в котором происходит их описание. Нумерация производится сквозная после слова «рисунок» внизу изображения посредине. Если к рисунку требуется название, то после цифры ставится тире и подписывается название, точка в конце не ставится. Сокращений в слове «рисунок» допускать нельзя.
Оформление таблиц в дипломе
Таблицы подписываются по правой стороне листа, указывается номер арабскими цифрами.
Как и на рисунки, на все таблицы идет ссылка, располагающаяся в тексте. При переносе таблицы на следующий лист делается запись «Таблица №… продолжение». Внутри запись ведется текстом TNR кегль 12.
Использование маркированных и нумерованных списков в дипломе
Запись списков в дипломной ведется при помощи маркера черта «–» или нумерации арабскими цифрами. Для удобства лучше воспользоваться автоматической маркировкой. Выступ списка составляет 0,5 см., отступ слева 0,5 см. Диплом в соответствии с ГОСТ невозможен без соответствующих мелочей.
Оформление приложений в дипломной работе
На приложения даются ссылки внутри текста, сами приложения помещаются после списка использованных источников. Оно располагается с новой страницы, в учет объема текста приложения не входят.
Посреди строки заглавными буквами пишется слово «приложение» и номер. В отличие от формул, таблиц и рисунков, номера приложения, пишутся заглавными буквами русского алфавита, начиная с первой, при этом следует исключить восемь букв, редко используемых при печати (Ъ, Ь; Ё; З; Й; Ч; О;Ы). Допускается также использование латинских букв, начиная с первой за исключением (I и O).
Далее под приложением строчными буквами вносится название. Приложения также как и вся работа могут разделяться на разделы и подразделы. В зависимости от их объема.
Оформление списка литературы в дипломе
В ГОСТе прописано, что список литературы должен обозначаться как «список использованных источников», сведения в тексте должны приводиться в том порядке, в котором они внесены в список.
Структура внесения авторов в список использованных источников такой:
- нормативные документы: гост, дата, номер, название;
- книги: вначале записываются авторы русских изданий по алфавиту, за ними редакторы, следом обозначаются иностранные авторы и редакторы: автор, название/редактор – первая буква названия города: аббревиатура университета, год издания – число страниц с.;
- периодические печатные издания (журналы; брошюры): автор название // название области конференции – год издания — № сборника – С. Страницы используемой статьи;
- электронные источники на съемных носителях: название статьи [Электронный ресурс]: съемный носитель;
- источники сети интернет: название статьи [Электронный ресурс]: адрес ссылки.
Как правильно оформлять формулы в дипломной работе
Данный аспект регулируется ГОСТом 7.32-2001 и нормативными документами конкретного ВУЗа, которые фиксируют следующие правила оформления:
- Использованию подлежат только общепринятые символы и сокращения, в противном случае – требуется дополнительная расшифровка.
- Существует негласное правило: одна формула – одна строка, даже если вы сравниваете две формулы между собой.
- Формулы должны быть отделены от остального текста, минимум – на один интервал.
- Если вам не хватило места, то формулу можно перенести, но завершать формулу на строке продолжать формулу на другой строке необходимо посредством математических знаков: знак сложения, вычитания, равенства и так далее. При этом важно также соблюдать правила форматирования: первую строку нужно выравнивать по левому краю, а вторую – по правому. Так формула будет более читабельна и менее объёмна.
- Если вам необходим знак умножения, то обозначать его точкой нельзя, только крестиком (буквой х).
- Если вы используете сложную формулу с дробями или другими элементами, которые утяжеляют конструкцию и делают её нечитабельной, то логичнее заменить какую-то часть формулы буквой. Букву необходимо расшифровать сразу после формулы таким образом: *формула*, ниже строчкой — *где…- это…*. Можно заменять несколько символов и даже записывать формулу полностью символами, если это упростит задачу восприятия и осмысления. Обозначения должны идти по порядку, для того, чтобы читающему не нужно было искать, какая буква что обозначает. В таком случае, достаточно читать формулу естественным образом, считывая при этом обозначения элементов. Для удобства рядом с буквой можно указывать единицу измерения.
- Разделять формулы в тексте, даже если они связаны, следует точкой с запятой. Особенно когда одна формула завершается цифрой, а другая начинается цифрой, либо формула содержит в себе взаимодополняющие равенства. В остальном же, и формулы, и текст считаются частями одной конструкции, поэтому независимо от формата повествования, используются стандартные правила расстановки пунктуационных знаков.
- Что касается оформления отсылок к расчётам, то их необходимо оформлять в тексте, используя круглые скобки. Например, «Уровень дохода горожан на 2019 год (12)».
Нумерация формул в тексте
В вашей работе может быть много формул, но нумеровать имеет смысл лишь те, к которым вы делаете отсылку по ходу повествования, в самом тексте.
Как уже было сказано ранее, оформлять такие ссылки необходимо при помощи круглых скобок. При этом важно учитывать то, что используются только арабские цифры.
Если формула растянулась на несколько строк, то нумерация ставится рядом с последней частью выражения, то есть по окончанию записи.
В зависимости от стандартов вашего учебного заведения, нумерация может быть сквозной и проходить через всю работу, либо быть постраничной или в пределах одной главы.
Если в работе много формул, то логичнее использовать несквозной вариант, ведь с простыми числами проще работать.
Но если формулы расположены по тексту неравномерно и часто очень сложно сориентироваться, и соотнести информацию, то вариант сквозной нумерации также применим.
Если вы располагаете формулы в приложениях, то их обозначения могут дополняться буквами. Таким образом, буква определяет позицию, а цифра – порядковый номер формулы в позиции.
Если имеет место группа формул, то они объединяются одним номером, при этом каждое выражение – это новая строка, а группа выражений обособляется фигурной скобкой. В таком случае порядковый номер формул указывается всё также в круглых скобках, но при этом выносится за фигурную скобку.
В этом случае могут использоваться также буквы, но, обратите внимание, что они уже не арабские, а русские.
Естественно, формулы могут разниться по своему значению. Если это формулы, которые категорически важны для повествования и для результата работы, то правила, указанные выше, для них актуальны.
Но есть и другой тип формул – те, которые важны не столько для результата, сколько для изложения самого процесса, этапов работы. Такие формулы обозначаются русскими буквами или звёздочками в круглых скобках.
Как создать и оформить формулу правильно
Как ни странно, но есть два способа это сделать. Обратите внимание, что для корректного оформления, вам нужно выбрать только один. Оформить в текстовом редакторе, а потом дописать что-то от руки – нельзя.
Первый способ предполагает то, что вы сделаете это вручную, при помощи чернил. Но на дворе 2019 год, да и по этому поводу могут возникнуть вопросы относительно ваших компетенций, в том числе – умением использовать достижения ИТ.
Поэтому оставим этот вариант как вариант на крайний случай.
Естественно, второй вариант – это воспользоваться текстовым редактором Microsoft Word. Данный редактор приспособлен ко всем нуждам студентов, а его интерфейс довольно прост, поэтому попробуйте самостоятельно понять, как и что делать. Но если не получается – не беда. Объясняем:
- В верхней панели выбираем блок «Вставка»;
- Справа сверху вы увидите блок «Формула», нажимаем и открывается редактор «Работа с формулами»;
- Производим настройку блока, в зависимости от необходимого типа формулы.
В редакторе есть стандартные символы, а есть и конструктор, который позволяет вам создавать свои формулы. Шрифт установлен по умолчанию, но вы, опять же, вольны выбирать тот, который вам наиболее подходит.
Если даже после наших инструкций, у вас не получилось разобраться, или ваша версия программы не позволяет делать и редактировать формулы, то воспользуйтесь функцией технической поддержки, либо обновите пакеты.
Оформление формул в курсовой
Практическая или экспериментальная часть курсового проекта имеет очень важное значение, особенно это касается студентов, которые обучаются на различных механических и технологических факультетах, а также на специальностях физико-математического и естественно научного профиля.
Оформление таких работ тесно связано как с чертежами, так и с математическими расчетами, где формулы являются основой исследования. Конечно, для студентов первых курсов работа с формулами (их правильное написание и оформление) весьма затруднительна, а сам текст курсовика нередко изобилует ошибками.
Студенты старших курсов активно пользуются инновационными достижениями, применяя современные компьютерные программы для составления формул различной степени сложности.
Положение в тексте и правила нумерации
Каждой новой формуле соответствует отдельная строка, которую ограничивают абзацными отступами с двух сторон, обособляя ее от текста работы. В результате вы получаете пустые строки сверху и снизу от формулы. Символьную запись размещают строго по центру строки.
Пример: БК12 = БК12 + УП2 + Са3
Если формулы не сопровождаются текстовыми комментариями, то несколько идущих подряд формул необходимо разделить запятыми.
Пример: РуП = Ммах – Мц, НоРмах =МКмах – К2
Правила нумерации формул предполагают использование арабских цифр. Сначала записываем формулу, а с правой стороны в круглых скобках ставим порядковый номер. По аналогии с нумерацией табличных и графических материалов, формулы нумеруют не только в основной части работы, но и в каждом разделе отдельно.
Тогда вы должны разделить порядковый номер формулы и номер раздела точкой. Следует отметить, что нумерация формул, помещенных в приложения, отличается от обычной.
Не забудьте указать обозначение приложения (используем буквы кириллицы или латиницы) и порядковый номер формулы, в качестве разделителя используем точку.
Пример: РКСАМ = Умах — ГЕП (1) РКСАМ = Умах — ГЕП (5.9)
РКСАМ = Умах — ГЕП (Б.8)
Правила переноса для математических формул
Часто бывает так, то ваши формулы содержат много коэффициентов и буквенных обозначений, поэтому могут не поместиться в одну строку. В таком случае формула переносится на следующую строку.
Для переноса формулы вам необходимо повторить знак действия на новой строке, где будет размещаться вторая часть формулы.
Для переноса символьной записи подходят любые знаки математических действий: «+», «-«, «*», «:», или знак равенства.
Пример: Х = S (12 + R)2 T + + (12 + in/180) (5)
Пояснительная запись и формулы
Как правило, математические формулы имеют различную степень сложности, а также насыщенность числовыми коэффициентами и буквенными обозначениями, которые необходимо сопровождать пояснительными записями. Тогда любой член аттестационной комиссии сможет понять суть ваших расчетов.
Пояснительную запись лучше начинать словом «где», которое размещают на новой строке, абзац и двоеточие ставить не нужно. Далее все значения, как буквенные, так и числовые, сопровождаются комментариями. Пояснение для каждого элемента формулы пишут с новой строки.
Порядок пояснительных записей определяется так: все комментарии дают в том порядке, как обозначения представлены в формуле.
Пример: Формула для расчёта комбинированных процентов, которые могут быть начислены за определенный период (3 — 5 лет):
G= S (1n + x) w (4) где S — сумма долга с процентами; G — сумма кредита; w — число лет;
x — годовой процент в долях.
Формула для расчёта обращения денежных единиц в количественном эквиваленте:
МД = ∑(БТ – 2К +СП – БС)/VS где МД — деньги (масса); Ебт — цена товара (сумма); 2К — товары в кредите; СП — срочные платежи; БС — операции в форме бартера;
VS — годовой оборот денег (показатель скорости)
Оформление ссылок
Связь текста вашей курсовой и математических расчетов или доказательств должна быть выражена в соответствующих ссылках на формулы. Приведем пример. Расчет специальных коэффициентов для начисления местного налога в зависимости от специализации района (туристический сбор и т. д.) в Южном федеральном округе был произведен по формуле (10).
Как правильно писать формулы?
Согласно требованиям ГОСТа для обозначения формул можно использовать кириллицу, латиницу или буквы греческого алфавита. Можно выделить два способа написания формул в научно-исследовательских работах. Первый способ – рукописный. Формулы пишут от руки черной ручкой (маркером, фломастером, чернилами).
Второй метод более современный, он связан с различным программным обеспечением, при помощи которого можно составлять как простые, так и комбинированные формулы. Для этих целей подойдут редакторы формул Microsoft Equations 3.0, Ooo Math, Formulator MathML Weaver.
Но в работе необходимо соблюдать единый стиль символьных записей (от руки или печатный), сочетание двух типов символов в одной формуле не допускается.
Также нужно знать, что для оформления этой части курсовой, вам понадобится достаточное количество времени, собранность и внимательность, иначе одна описка или опечатка может сделать все ваши расчеты ошибочными.
Оформление формул в научной статье ВАК
Публикация научных статей ВАК в рецензируемом журнале требует от автора не только представления в редакцию уникального оригинального текста, но и его правильного оформления в соответствие с ГОСТ и требованиями журнала. Особенно это касается рукописей, в которых содержится много сокращений, формул и таблиц. В сегодняшнем материале мы приводим основные правила подготовки формул для публикации в журнале ВАК.
Требования ВАК к оформлению формул
Многие авторы статей получают замечания, связанные с неправильным оформлением рукописи. Часто требования редакций журналов ВАК к оформлению формул совпадают с требованиями ГОСТ, поэтому целесообразно руководствоваться положениями последнего при оформлении статьи для публикации.
- Шрифт текста в формулах должен совпадать со шрифтом основного текста. Если формулы вставляются в текст из разных файлов, приведите их к единообразию. Обратите внимание! Многие издательства публикуют требования к тексту рукописи, где указываются параметры шрифта.
- Если вы используете для набора формулы редактор, обратите внимание, что нельзя оформлять формулы согласно ГОСТ во встроенном редакторе формул Microsoft Word 2007. Для набора сложных многострочных формул используйте Microsoft Equation или MathType.
- Если формула многострочная, то перенести ее на следующую строку можно только на знаке выполняемой операции. При этом необходимо повторить знак операции на следующей строке. Если формула переносится на знаке умножения, то следует применить знак «х».
- В одной формуле не разрешается одновременное использование машинописных и рукописных символов. Если формула оформляется рукописно, изучите требования к оформлению рисунков и таблиц.
Если употребляется особая система наименования слов и сокращений, то в тексте должен быть приведен список принятых сокращений, который размещается после основного текста документа перед списком принятых в нем терминов. Перечень допустимых сокращений приведен в ГОСТ 2.316.
В качестве символов в формулах применяются обозначения, установленные ГОСТ. Пояснения к символам, если они не расшифровываются в предшествующем тексте, даются прямо под формулой. Определение каждого символа дается в той последовательности, в которой они стоят в формуле. Верхняя строка пояснений начинается со слова где. Причем двоеточие после него не ставится.
Общие сведения об уравнениях
Уравнения — одна из сложных тем для усвоения, но при этом они являются достаточно мощным инструментом для решения большинства задач.
С помощью уравнений описываются различные процессы, протекающие в природе. Уравнения широко применяются в других науках: в экономике, физике, биологии и химии.
В данном уроке мы попробуем понять суть простейших уравнений, научимся выражать неизвестные и решим несколько уравнений. По мере усвоения новых материалов, уравнения будут усложняться, поэтому понять основы очень важно.
Что такое уравнение?
Уравнение — это равенство, содержащее в себе переменную, значение которой требуется найти. Это значение должно быть таким, чтобы при его подстановке в исходное уравнение получалось верное числовое равенство.
Например выражение 3 + 2 = 5 является равенством. При вычислении левой части получается верное числовое равенство 5 = 5 .
А вот равенство 3 + x = 5 является уравнением, поскольку содержит в себе переменную x , значение которой можно найти. Значение должно быть таким, чтобы при подстановке этого значения в исходное уравнение, получилось верное числовое равенство.
Другими словами, мы должны найти такое значение, при котором знак равенства оправдал бы свое местоположение — левая часть должна быть равна правой части.
Уравнение 3 + x = 5 является элементарным. Значение переменной x равно числу 2. При любом другом значении равенство соблюдáться не будет
Говорят, что число 2 является корнем или решением уравнения 3 + x = 5
Корень или решение уравнения — это значение переменной, при котором уравнение обращается в верное числовое равенство.
Корней может быть несколько или не быть совсем. Решить уравнение означает найти его корни или доказать, что корней нет.
Переменную, входящую в уравнение, иначе называют неизвестным. Вы вправе называть как вам удобнее. Это синонимы.
Примечание. Словосочетание «решить уравнение» говорит самó за себя. Решить уравнение означает «уравнять» равенство — сделать его сбалансированным, чтобы левая часть равнялась правой части.
Выразить одно через другое
Изучение уравнений по традиции начинается с того, чтобы научиться выражать одно число, входящее в равенство, через ряд других. Давайте не будем нарушать эту традицию и поступим также.
Рассмотрим следующее выражение:
Данное выражение является суммой чисел 8 и 2. Значение данного выражения равно 10
Получили равенство. Теперь можно выразить любое число из этого равенства через другие числа, входящие в это же равенство. К примеру, выразим число 2.
Чтобы выразить число 2, нужно задать вопрос: «что нужно сделать с числами 10 и 8, чтобы получить число 2». Понятно, что для получения числа 2, нужно из числа 10 вычесть число 8.
Так и делаем. Записываем число 2 и через знак равенства говорим, что для получения этого числа 2 мы из числа 10 вычли число 8:
Мы выразили число 2 из равенства 8 + 2 = 10 . Как видно из примера, ничего сложного в этом нет.
При решении уравнений, в частности при выражении одного числа через другие, знак равенства удобно заменять на слово «есть». Делать это нужно мысленно, а не в самом выражении.
Так, выражая число 2 из равенства 8 + 2 = 10 мы получили равенство 2 = 10 − 8 . Данное равенство можно прочесть так:
2 есть 10 − 8
То есть знак = заменен на слово «есть». Более того, равенство 2 = 10 − 8 можно перевести с математического языка на полноценный человеческий язык. Тогда его можно будет прочитать следующим образом:
Число 2 есть разность числа 10 и числа 8
Число 2 есть разница между числом 10 и числом 8.
Но мы ограничимся лишь заменой знака равенства на слово «есть», и то будем делать это не всегда. Элементарные выражения можно понимать и без перевода математического языка на язык человеческий.
Вернём получившееся равенство 2 = 10 − 8 в первоначальное состояние:
Выразим в этот раз число 8. Что нужно сделать с остальными числами, чтобы получить число 8? Верно, нужно из числа 10 вычесть число 2
Вернем получившееся равенство 8 = 10 − 2 в первоначальное состояние:
В этот раз выразим число 10. Но оказывается, что десятку выражать не нужно, поскольку она уже выражена. Достаточно поменять местами левую и правую часть, тогда получится то, что нам нужно:
Пример 2. Рассмотрим равенство 8 − 2 = 6
Выразим из этого равенства число 8. Чтобы выразить число 8 остальные два числа нужно сложить:
Вернем получившееся равенство 8 = 6 + 2 в первоначальное состояние:
Выразим из этого равенства число 2. Чтобы выразить число 2, нужно из 8 вычесть 6
Пример 3. Рассмотрим равенство 3 × 2 = 6
Выразим число 3. Чтобы выразить число 3, нужно 6 разделить 2
Вернем получившееся равенство 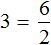
Выразим из этого равенства число 2. Чтобы выразить число 2, нужно 6 разделить 3
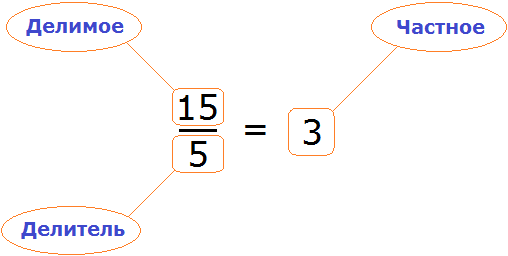
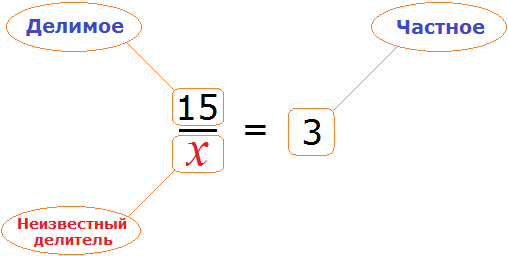
Пример 4. Рассмотрим равенство
Выразим из этого равенства число 15. Чтобы выразить число 15, нужно перемножить числа 3 и 5
Вернем получившееся равенство 15 = 3 × 5 в первоначальное состояние:
Выразим из этого равенства число 5. Чтобы выразить число 5, нужно 15 разделить 3
Правила нахождения неизвестных
Рассмотрим несколько правил нахождения неизвестных. Возможно, они вам знакомы, но не мешает повторить их ещё раз. В дальнейшем их можно будет забыть, поскольку мы научимся решать уравнения, не применяя эти правила.
Вернемся к первому примеру, который мы рассматривали в предыдущей теме, где в равенстве 8 + 2 = 10 требовалось выразить число 2.
В равенстве 8 + 2 = 10 числа 8 и 2 являются слагаемыми, а число 10 — суммой.
Чтобы выразить число 2, мы поступили следующим образом:
То есть из суммы 10 вычли слагаемое 8.
Теперь представим, что в равенстве 8 + 2 = 10 вместо числа 2 располагается переменная x
В этом случае равенство 8 + 2 = 10 превращается в уравнение 8 + x = 10 , а переменная x берет на себя роль так называемого неизвестного слагаемого
Наша задача найти это неизвестное слагаемое, то есть решить уравнение 8 + x = 10 . Для нахождения неизвестного слагаемого предусмотрено следующее правило:
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
Что мы в принципе и сделали, когда выражали двойку в равенстве 8 + 2 = 10 . Чтобы выразить слагаемое 2, мы из суммы 10 вычли другое слагаемое 8
А сейчас, чтобы найти неизвестное слагаемое x , мы должны из суммы 10 вычесть известное слагаемое 8:
Если вычислить правую часть получившегося равенства, то можно узнать чему равна переменная x
Мы решили уравнение. Значение переменной x равно 2 . Для проверки значение переменной x отправляют в исходное уравнение 8 + x = 10 и подставляют вместо x. Так желательно поступать с любым решённым уравнением, поскольку нельзя быть точно уверенным, что уравнение решено правильно:
В результате получается верное числовое равенство. Значит уравнение решено правильно.
Это же правило действовало бы в случае, если неизвестным слагаемым было бы первое число 8.
В этом уравнении x — это неизвестное слагаемое, 2 — известное слагаемое, 10 — сумма. Чтобы найти неизвестное слагаемое x , нужно из суммы 10 вычесть известное слагаемое 2
Вернемся ко второму примеру из предыдущей темы, где в равенстве 8 − 2 = 6 требовалось выразить число 8.
В равенстве 8 − 2 = 6 число 8 это уменьшаемое, число 2 — вычитаемое, число 6 — разность
Чтобы выразить число 8, мы поступили следующим образом:
То есть сложили разность 6 и вычитаемое 2.
Теперь представим, что в равенстве 8 − 2 = 6 вместо числа 8 располагается переменная x
В этом случае переменная x берет на себя роль так называемого неизвестного уменьшаемого
Для нахождения неизвестного уменьшаемого предусмотрено следующее правило:
Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое.
Что мы и сделали, когда выражали число 8 в равенстве 8 − 2 = 6 . Чтобы выразить уменьшаемое 8, мы к разности 6 прибавили вычитаемое 2.
А сейчас, чтобы найти неизвестное уменьшаемое x , мы должны к разности 6 прибавить вычитаемое 2
Если вычислить правую часть, то можно узнать чему равна переменная x
Теперь представим, что в равенстве 8 − 2 = 6 вместо числа 2 располагается переменная x
В этом случае переменная x берет на себя роль неизвестного вычитаемого
Для нахождения неизвестного вычитаемого предусмотрено следующее правило:
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.
Что мы и сделали, когда выражали число 2 в равенстве 8 − 2 = 6. Чтобы выразить число 2, мы из уменьшаемого 8 вычли разность 6.
А сейчас, чтобы найти неизвестное вычитаемое x, нужно опять же из уменьшаемого 8 вычесть разность 6
Вычисляем правую часть и находим значение x
Вернемся к третьему примеру из предыдущей темы, где в равенстве 3 × 2 = 6 мы пробовали выразить число 3.
В равенстве 3 × 2 = 6 число 3 — это множимое, число 2 — множитель, число 6 — произведение
Чтобы выразить число 3 мы поступили следующим образом:
То есть разделили произведение 6 на множитель 2.
Теперь представим, что в равенстве 3 × 2 = 6 вместо числа 3 располагается переменная x
В этом случае переменная x берет на себя роль неизвестного множимого.
Для нахождения неизвестного множимого предусмотрено следующее правило:
Чтобы найти неизвестное множимое, нужно произведение разделить на множитель.
Что мы и сделали, когда выражали число 3 из равенства 3 × 2 = 6 . Произведение 6 мы разделили на множитель 2.
А сейчас для нахождения неизвестного множимого x , нужно произведение 6 разделить на множитель 2.
Вычисление правой части позволяет нам найти значение переменной x
Это же правило применимо в случае, если переменная x располагается вместо множителя, а не множимого. Представим, что в равенстве 3 × 2 = 6 вместо числа 2 располагается переменная x .
В этом случае переменная x берет на себя роль неизвестного множителя. Для нахождения неизвестного множителя предусмотрено такое же, что и для нахождения неизвестного множимого, а именно деление произведения на известный множитель:
Чтобы найти неизвестный множитель, нужно произведение разделить на множимое.
Что мы и сделали, когда выражали число 2 из равенства 3 × 2 = 6 . Тогда для получения числа 2 мы разделили произведение 6 на множимое 3.
А сейчас для нахождения неизвестного множителя x мы разделили произведение 6 на множимое 3.
Вычисление правой части равенства 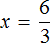
Множимое и множитель вместе называют сомножителями. Поскольку правила нахождения множимого и множителя совпадают, мы можем сформулировать общее правило нахождения неизвестного сомножителя:
Чтобы найти неизвестный сомножитель, нужно произведение разделить на известный сомножитель.
Например, решим уравнение 9 × x = 18 . Переменная x является неизвестным сомножителем. Чтобы найти этот неизвестный сомножитель, нужно произведение 18 разделить на известный сомножитель 9
Отсюда 
Решим уравнение x × 3 = 27 . Переменная x является неизвестным сомножителем. Чтобы найти этот неизвестный сомножитель, нужно произведение 27 разделить на известный сомножитель 3
Отсюда 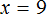
Вернемся к четвертому примеру из предыдущей темы, где в равенстве 
Чтобы выразить число 15 мы поступили следующим образом:
То есть умножили частное 3 на делитель 5.
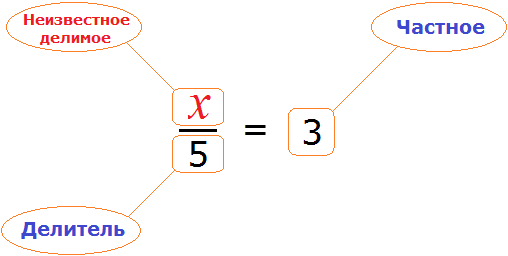
Теперь представим, что в равенстве 
В этом случае переменная x берет на себя роль неизвестного делимого.
Для нахождения неизвестного делимого предусмотрено следующее правило:
Чтобы найти неизвестное делимое, нужно частное умножить на делитель.
Что мы и сделали, когда выражали число 15 из равенства 
А сейчас, чтобы найти неизвестное делимое x , нужно частное 3 умножить на делитель 5
Вычислим правую часть получившегося равенства. Так мы узнаем чему равна переменная x .
Теперь представим, что в равенстве 
В этом случае переменная x берет на себя роль неизвестного делителя.
Для нахождения неизвестного делителя предусмотрено следующее правило:
Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
Что мы и сделали, когда выражали число 5 из равенства 
А сейчас, чтобы найти неизвестный делитель x , нужно делимое 15 разделить на частное 3
Вычислим правую часть получившегося равенства. Так мы узнаем чему равна переменная x .
Итак, для нахождения неизвестных мы изучили следующие правила:
- Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое;
- Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое;
- Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность;
- Чтобы найти неизвестное множимое, нужно произведение разделить на множитель;
- Чтобы найти неизвестный множитель, нужно произведение разделить на множимое;
- Чтобы найти неизвестное делимое, нужно частное умножить на делитель;
- Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
Компоненты
Компонентами мы будем называть числа и переменные, входящие в равенство
Так, компонентами сложения являются слагаемые и сумма
Компонентами вычитания являются уменьшаемое, вычитаемое и разность
Компонентами умножения являются множимое, множитель и произведение
Компонентами деления являются делимое, делитель и частное
В зависимости от того, с какими компонентами мы будем иметь дело, будут применяться соответствующие правила нахождения неизвестных. Эти правила мы изучили в предыдущей теме. При решении уравнений желательно знать эти правило наизусть.
Пример 1. Найти корень уравнения 45 + x = 60
45 — слагаемое, x — неизвестное слагаемое, 60 — сумма. Имеем дело с компонентами сложения. Вспоминаем, что для нахождения неизвестного слагаемого, нужно из суммы вычесть известное слагаемое:
Вычислим правую часть, получим значение x равное 15
Значит корень уравнения 45 + x = 60 равен 15.
Чаще всего неизвестное слагаемое необходимо привести к виду при котором его можно было бы выразить.
Пример 2. Решить уравнение
Здесь в отличие от предыдущего примера, неизвестное слагаемое нельзя выразить сразу, поскольку оно содержит коэффициент 2. Наша задача привести это уравнение к виду при котором можно было бы выразить x
В данном примере мы имеем дело с компонентами сложения — слагаемыми и суммой. 2x — это первое слагаемое, 4 — второе слагаемое, 8 — сумма.
При этом слагаемое 2x содержит переменную x . После нахождения значения переменной x слагаемое 2x примет другой вид. Поэтому слагаемое 2x можно полностью принять за неизвестное слагаемое:
Теперь применяем правило нахождения неизвестного слагаемого. Вычитаем из суммы известное слагаемое:
Вычислим правую часть получившегося уравнения:
Мы получили новое уравнение 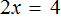
При этом переменная x является не просто множителем, а неизвестным множителем
Чтобы найти этот неизвестный множитель, нужно произведение разделить на множимое:
Вычислим правую часть, получим значение переменной x
Для проверки найденный корень отправим в исходное уравнение 
Получили верное числовое равенство. Значит уравнение решено правильно.
Пример 3. Решить уравнение 3x + 9x + 16x = 56
Cразу выразить неизвестное x нельзя. Сначала нужно привести данное уравнение к виду при котором его можно было бы выразить.
Приведем подобные слагаемые в левой части данного уравнения:
Имеем дело с компонентами умножения. 28 — множимое, x — множитель, 56 — произведение. При этом x является неизвестным множителем. Чтобы найти неизвестный множитель, нужно произведение разделить на множимое:
Отсюда x равен 2
Равносильные уравнения
В предыдущем примере при решении уравнения 3x + 9x + 16x = 56 , мы привели подобные слагаемые в левой части уравнения. В результате получили новое уравнение 28x = 56 . Старое уравнение 3x + 9x + 16x = 56 и получившееся новое уравнение 28x = 56 называют равносильными уравнениями, поскольку их корни совпадают.
Уравнения называют равносильными, если их корни совпадают.
Проверим это. Для уравнения 3x + 9x + 16x = 56 мы нашли корень равный 2 . Подставим этот корень сначала в уравнение 3x + 9x + 16x = 56 , а затем в уравнение 28x = 56 , которое получилось в результате приведения подобных слагаемых в левой части предыдущего уравнения. Мы должны получить верные числовые равенства
Согласно порядку действий, в первую очередь выполняется умножение:
Подставим корень 2 во второе уравнение 28x = 56
Видим, что у обоих уравнений корни совпадают. Значит уравнения 3x + 9x + 16x = 56 и 28x = 56 действительно являются равносильными.
Для решения уравнения 3x + 9x + 16x = 56 мы воспользовались одним из тождественных преобразований — приведением подобных слагаемых. Правильное тождественное преобразование уравнения позволило нам получить равносильное уравнение 28x = 56 , которое проще решать.
Из тождественных преобразований на данный момент мы умеем только сокращать дроби, приводить подобные слагаемые, выносить общий множитель за скобки, а также раскрывать скобки. Существуют и другие преобразования, которые следует знать. Но для общего представления о тождественных преобразованиях уравнений, изученных нами тем вполне хватает.
Рассмотрим некоторые преобразования, которые позволяют получить равносильное уравнение
Если к обеим частям уравнения прибавить одно и то же число, то получится уравнение равносильное данному.
Если из обеих частей уравнения вычесть одно и то же число, то получится уравнение равносильное данному.
Другими словами, корень уравнения не изменится, если к обеим частям данного уравнения прибавить (или вычесть из обеих частей) одно и то же число.
Пример 1. Решить уравнение
Вычтем из обеих частей уравнения число 10
Приведем подобные слагаемые в обеих частях:
Получили уравнение 5x = 10 . Имеем дело с компонентами умножения. Чтобы найти неизвестный сомножитель x , нужно произведение 10 разделить на известный сомножитель 5.
Отсюда 
Вернемся к исходному уравнению 
Получили верное числовое равенство. Значит уравнение решено правильно.
Решая уравнение 
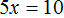

Пример 2. Решить уравнение 4(x + 3) = 16
Раскроем скобки в левой части равенства:
Вычтем из обеих частей уравнения число 12
Приведем подобные слагаемые в обеих частях уравнения:
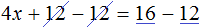
Получили уравнение 4x = 4 . Имеем дело с компонентами умножения. Чтобы найти неизвестный сомножитель x , нужно произведение 4 разделить на известный сомножитель 4
Отсюда
Вернемся к исходному уравнению 4(x + 3) = 16 и подставим вместо x найденное значение 1
Получили верное числовое равенство. Значит уравнение решено правильно.
Решая уравнение 4(x + 3) = 16 мы вычли из обеих частей уравнения число 12 . В результате получили равносильное уравнение 4x = 4 . Корень этого уравнения, как и уравнения 4(x + 3) = 16 так же равен 1
Пример 3. Решить уравнение
Раскроем скобки в левой части равенства:
Прибавим к обеим частям уравнения число 8
Приведем подобные слагаемые в обеих частях уравнения:
В левой части останется 2x , а в правой части число 9
В получившемся уравнении 2x = 9 выразим неизвестное слагаемое x
Отсюда
Вернемся к исходному уравнению 
Получили верное числовое равенство. Значит уравнение решено правильно.
Решая уравнение 
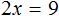

Следующее правило, которое позволяет получить равносильное уравнение, выглядит следующим образом
Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение равносильное данному.
То есть корень уравнения не изменится, если мы перенесем слагаемое из одной части уравнения в другую, изменив его знак. Это свойство является одним из важных и одним из часто используемых при решении уравнений.
Рассмотрим следующее уравнение:
Корень данного уравнения равен 2. Подставим вместо x этот корень и проверим получается ли верное числовое равенство
Получается верное равенство. Значит число 2 действительно является корнем уравнения 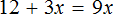
Теперь попробуем поэкспериментировать со слагаемыми этого уравнения, перенося их из одной части в другую, изменяя знаки.
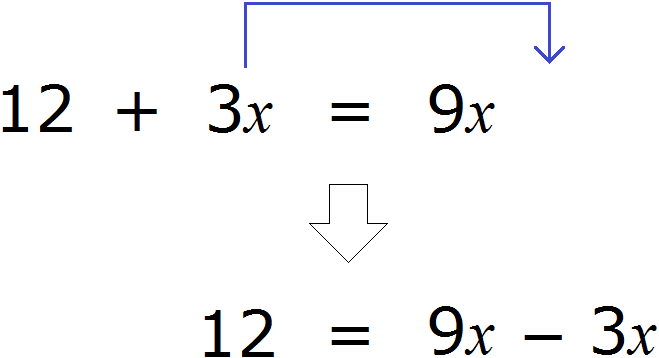
Например, слагаемое 3x располагается в левой части равенства. Перенесём его в правую часть, изменив знак на противоположный:
Получилось уравнение 12 = 9x − 3x . Приведем подобные слагаемые в правой части данного уравнения:
Имеем дело с компонентами умножения. Переменная x является неизвестным сомножителем. Найдём этот известный сомножитель:
Отсюда x = 2 . Как видим, корень уравнения не изменился. Значит уравнения 12 + 3x = 9x и 12 = 9x − 3x являются равносильными.
На самом деле данное преобразование является упрощенным методом предыдущего преобразования, где к обеим частям уравнения прибавлялось (или вычиталось) одно и то же число.
Мы сказали, что в уравнении 12 + 3x = 9x слагаемое 3x было перенесено в правую часть, изменив знак. В реальности же происходило следующее: из обеих частей уравнения вычли слагаемое 3x
Затем в левой части были приведены подобные слагаемые и получено уравнение 12 = 9x − 3x. Затем опять были приведены подобные слагаемые, но уже в правой части, и получено уравнение 12 = 6x.
Но так называемый «перенос» более удобен для подобных уравнений, поэтому он и получил такое широкое распространение. Решая уравнения, мы часто будем пользоваться именно этим преобразованием.
Равносильными также являются уравнения 12 + 3x = 9x и 3x − 9x = −12 . В этот раз в уравнении 12 + 3x = 9x слагаемое 12 было перенесено в правую часть, а слагаемое 9x в левую. Не следует забывать, что знаки этих слагаемых были изменены во время переноса
Следующее правило, которое позволяет получить равносильное уравнение, выглядит следующим образом:
Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю, то получится уравнение равносильное данному.
Другими словами, корни уравнения не изменятся, если обе его части умножить или разделить на одно и то же число. Это действие часто применяется тогда, когда нужно решить уравнение содержащее дробные выражения.
Сначала рассмотрим примеры, в которых обе части уравнения будут умножаться на одно и то же число.
Пример 1. Решить уравнение
При решении уравнений, содержащих дробные выражения, сначала принято упростить это уравнение.
В данном случае мы имеем дело именно с таким уравнением. В целях упрощения данного уравнения обе его части можно умножить на 8:
Мы помним, что для умножения дроби на число, нужно числитель данной дроби умножить на это число. У нас имеются две дроби и каждая из них умножается на число 8. Наша задача умножить числители дробей на это число 8
Теперь происходит самое интересное. В числителях и знаменателях обеих дробей содержится множитель 8, который можно сократить на 8. Это позволит нам избавиться от дробного выражения:
В результате останется простейшее уравнение
Ну и нетрудно догадаться, что корень этого уравнения равен 4
Вернемся к исходному уравнению 
Получается верное числовое равенство. Значит уравнение решено правильно.
При решении данного уравнения мы умножили обе его части на 8. В результате получили уравнение 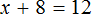

Множитель на который умножаются обе части уравнения принято записывать перед частью уравнения, а не после неё. Так, решая уравнение 
От этого корень уравнения не изменился, но если бы мы сделали это находясь в школе, то нам сделали бы замечание, поскольку в алгебре множитель принято записывать перед тем выражением, с которым он перемножается. Поэтому умножение обеих частей уравнения 
Пример 2. Решить уравнение
Умнóжим обе части уравнения на 15
В левой части множители 15 можно сократить на 15, а в правой части множители 15 и 5 можно сократить на 5
Перепишем то, что у нас осталось:
Раскроем скобки в правой части уравнения:
Перенесем слагаемое x из левой части уравнения в правую часть, изменив знак. А слагаемое 15 из правой части уравнения перенесем в левую часть, опять же изменив знак:
Приведем подобные слагаемые в обеих частях, получим
Имеем дело с компонентами умножения. Переменная x является неизвестным сомножителем. Найдём этот известный сомножитель:
Отсюда
Вернемся к исходному уравнению 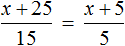
Получается верное числовое равенство. Значит уравнение решено правильно. При решении данного уравнения мы умножили обе го части на 15 . Далее выполняя тождественные преобразования, мы получили уравнение 10 = 2x . Корень этого уравнения, как и уравнения 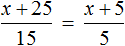
Пример 3. Решить уравнение
Умнóжим обе части уравнения на 3
В левой части можно сократить две тройки, а правая часть будет равна 18
Останется простейшее уравнение 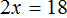
Отсюда
Вернемся к исходному уравнению 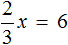
Получается верное числовое равенство. Значит уравнение решено правильно.
Пример 4. Решить уравнение
Умнóжим обе части уравнения на 6
В левой части уравнения раскроем скобки. В правой части множитель 6 можно поднять в числитель:
Сократим в обеих частях уравнениях то, что можно сократить:
Перепишем то, что у нас осталось:
Раскроем скобки в обеих частях уравнения:
Воспользуемся переносом слагаемых. Слагаемые, содержащие неизвестное x , сгруппируем в левой части уравнения, а слагаемые свободные от неизвестных — в правой:
Приведем подобные слагаемые в обеих частях:
Теперь найдем значение переменной x . Для этого разделим произведение 28 на известный сомножитель 7
Вернемся к исходному уравнению 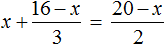
Получилось верное числовое равенство. Значит уравнение решено правильно.
Пример 5. Решить уравнение
Раскроем скобки в обеих частях уравнения там, где это можно:
Умнóжим обе части уравнения на 15
Раскроем скобки в обеих частях уравнения:
Сократим в обеих частях уравнения, то что можно сократить:
Перепишем то, что у нас осталось:
Раскроем скобки там, где это можно:
Воспользуемся переносом слагаемых. Слагаемые, содержащие неизвестное, сгруппируем в левой части уравнения, а слагаемые, свободные от неизвестных — в правой. Не забываем, что во время переноса, слагаемые меняют свои знаки на противоположные:
Приведем подобные слагаемые в обеих частях уравнения:
Найдём значение x
В получившемся ответе можно выделить целую часть:
Вернемся к исходному уравнению и подставим вместо x найденное значение
Получается довольно громоздкое выражение. Воспользуемся переменными. Левую часть равенства занесем в переменную A , а правую часть равенства в переменную B
Наша задача состоит в том, чтобы убедиться равна ли левая часть правой. Другими словами, доказать равенство A = B
Найдем значение выражения, находящегося в переменной А.
Значение переменной А равно 

Видим, что значение переменной B , как и значение переменной A равно 
Теперь попробуем не умножать обе части уравнения на одно и то же число, а делить.
Рассмотрим уравнение 30x + 14x + 14 = 70x − 40x + 42 . Решим его обычным методом: слагаемые, содержащие неизвестные, сгруппируем в левой части уравнения, а слагаемые, свободные от неизвестных — в правой. Далее выполняя известные тождественные преобразования, найдем значение x
Подставим найденное значение 2 вместо x в исходное уравнение:
Теперь попробуем разделить все слагаемые уравнения 30x + 14x + 14 = 70x − 40x + 42 на какое-нибудь число. Замечаем, что все слагаемые этого уравнения имеют общий множитель 2. На него и разделим каждое слагаемое:
Выполним сокращение в каждом слагаемом:
Перепишем то, что у нас осталось:
Решим это уравнение, пользуясь известными тождественными преобразованиями:
Получили корень 2 . Значит уравнения 15x + 7x + 7 = 35x − 20x + 21 и 30x + 14x + 14 = 70x − 40x + 42 равносильны.
Деление обеих частей уравнения на одно и то же число позволяет освобождать неизвестное от коэффициента. В предыдущем примере когда мы получили уравнение 7x = 14 , нам потребовалось разделить произведение 14 на известный сомножитель 7. Но если бы мы в левой части освободили неизвестное от коэффициента 7, корень нашелся бы сразу. Для этого достаточно было разделить обе части на 7
Этим методом мы тоже будем пользоваться часто.
Умножение на минус единицу
Если обе части уравнения умножить на минус единицу, то получится уравнение равносильное данному.
Это правило следует из того, что от умножения (или деления) обеих частей уравнения на одно и то же число, корень данного уравнения не меняется. А значит корень не поменяется если обе его части умножить на −1 .
Данное правило позволяет поменять знаки всех компонентов, входящих в уравнение. Для чего это нужно? Опять же, чтобы получить равносильное уравнение, которое проще решать.
Рассмотрим уравнение 
Прибавим к обеим частям уравнения число 5
Приведем подобные слагаемые:
А теперь вспомним про коэффициент буквенного выражения. Что же представляет собой левая часть уравнения 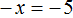
То есть минус, стоящий перед переменной x, относится не к самой переменной x , а к единице, которую мы не видим, поскольку коэффициент 1 принято не записывать. Это означает, что уравнение 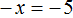
Имеем дело с компонентами умножения. Чтобы найти х , нужно произведение −5 разделить на известный сомножитель −1 .
или разделить обе части уравнения на −1 , что еще проще
Итак, корень уравнения 
Получилось верное числовое равенство. Значит уравнение решено верно.
Теперь попробуем умножить обе части уравнения 
После раскрытия скобок в левой части образуется выражение 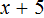
Корень этого уравнения, как и уравнения 
Значит уравнения 
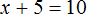
Пример 2. Решить уравнение
В данном уравнении все компоненты являются отрицательными. С положительными компонентами работать удобнее, чем с отрицательными, поэтому поменяем знаки всех компонентов, входящих в уравнение 
Понятно, что от умножения на −1 любое число поменяет свой знак на противоположный. Поэтому саму процедуру умножения на −1 и раскрытие скобок подробно не расписывают, а сразу записывают компоненты уравнения с противоположными знаками.
Так, умножение уравнения 
либо можно просто поменять знаки всех компонентов:
Получится то же самое, но разница будет в том, что мы сэкономим себе время.
Итак, умножив обе части уравнения 
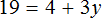
Когда корень найден, переменную обычно записывают в левой части, а её значение в правой, что мы и сделали.
Пример 3. Решить уравнение
Умнóжим обе части уравнения на −1 . Тогда все компоненты поменяют свои знаки на противоположные:
Из обеих частей получившегося уравнения вычтем 2x и приведем подобные слагаемые:
Прибавим к обеим частям уравнения единицу и приведем подобные слагаемые:
Приравнивание к нулю
Недавно мы узнали, что если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение равносильное данному.
А что будет если перенести из одной части в другую не одно слагаемое, а все слагаемые? Верно, в той части откуда забрали все слагаемые останется ноль. Иными словами, не останется ничего.
В качестве примера рассмотрим уравнение 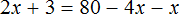
Теперь попробуем решить это же уравнение, приравняв все его компоненты к нулю. Для этого перенесем все слагаемые из правой части в левую, изменив знаки:
Приведем подобные слагаемые в левой части:
Прибавим к обеим частям 77 , и разделим обе части на 7
Альтернатива правилам нахождения неизвестных
Очевидно, что зная о тождественных преобразованиях уравнений, можно не заучивать наизусть правила нахождения неизвестных.
К примеру, для нахождения неизвестного в уравнении 
Но если в уравнении 
Уравнения вида 
Но можно воспользоваться тождественными преобразованиями, которые мы сегодня изучили. В уравнении 
Далее разделить обе части на 2
В левой части уравнения сократятся две двойки. Правая часть будет равна 2. Отсюда 
Либо можно было из обеих частей уравнения вычесть 4. Тогда получилось бы следующее:
В случае с уравнениями вида 
Первое решение намного короче и аккуратнее. Второе решение можно значительно укоротить, если выполнить деление в уме.
Тем не менее, необходимо знать оба метода, и только затем использовать тот, который больше нравится.
Когда корней несколько
Уравнение может иметь несколько корней. Например уравнение x(x + 9) = 0 имеет два корня: 0 и −9 .
В уравнении x(x + 9) = 0 нужно было найти такое значение x при котором левая часть была бы равна нулю. В левой части этого уравнения содержатся выражения x и (x + 9) , которые являются сомножителями. Из законов умножения мы знаем, что произведение равно нулю, если хотя бы один из сомножителей равен нулю (или первый сомножитель или второй).
То есть в уравнении x(x + 9) = 0 равенство будет достигаться, если x будет равен нулю или (x + 9) будет равно нулю.
Приравняв к нулю оба этих выражения, мы сможем найти корни уравнения x(x + 9) = 0 . Первый корень, как видно из примера, нашелся сразу. Для нахождения второго корня нужно решить элементарное уравнение x + 9 = 0 . Несложно догадаться, что корень этого уравнения равен −9 . Проверка показывает, что корень верный:
Пример 2. Решить уравнение
Данное уравнение имеет два корня: 1 и 2. Левая часть уравнения является произведение выражений (x − 1) и (x − 2) . А произведение равно нулю, если хотя бы один из сомножителей равен нулю (или сомножитель (x − 1) или сомножитель (x − 2) ).
Найдем такое x при котором выражения (x − 1) или (x − 2) обращаются в нули:
Подставляем по-очереди найденные значения в исходное уравнение 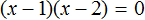
Когда корней бесконечно много
Уравнение может иметь бесконечно много корней. То есть подставив в такое уравнение любое число, мы получим верное числовое равенство.
Пример 1. Решить уравнение
Корнем данного уравнения является любое число. Если раскрыть скобки в левой части уравнения и привести подобные слагаемые, то получится равенство 14 = 14 . Это равенство будет получаться при любом x
Пример 2. Решить уравнение
Корнем данного уравнения является любое число. Если раскрыть скобки в левой части уравнения, то получится равенство 10x + 12 = 10x + 12. Это равенство будет получаться при любом x
Когда корней нет
Случается и так, что уравнение вовсе не имеет решений, то есть не имеет корней. Например уравнение 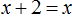
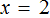
Пусть
Пример 2. Решить уравнение
Раскроем скобки в левой части равенства:
Приведем подобные слагаемые:
Видим, что левая часть не равна правой части. И так будет при любом значении y . Например, пусть y = 3 .
Буквенные уравнения
Уравнение может содержать не только числа с переменными, но и буквы.
Например, формула нахождения скорости является буквенным уравнением:
Данное уравнение описывает скорость движения тела при равноускоренном движении.
Полезным навыком является умение выразить любой компонент, входящий в буквенное уравнение. Например, чтобы из уравнения 
Умнóжим обе части уравнения 
В правой части переменные t сократим на t и перепишем то, что у нас осталось:
В получившемся уравнении левую и правую часть поменяем местами:
У нас получилась формула нахождения расстояния, которую мы изучали ранее.
Попробуем из уравнения 
Умнóжим обе части уравнения на t
В правой части переменные t сократим на t и перепишем то, что у нас осталось:
В получившемся уравнении v × t = s обе части разделим на v
В левой части переменные v сократим на v и перепишем то, что у нас осталось:
У нас получилась формула определения времени, которую мы изучали ранее.
Предположим, что скорость поезда равна 50 км/ч
А расстояние равно 100 км
Тогда буквенное уравнение 
Из этого уравнения можно найти время. Для этого нужно суметь выразить переменную t . Можно воспользоваться правилом нахождения неизвестного делителя, разделив делимое на частное и таким образом определить значение переменной t
либо можно воспользоваться тождественными преобразованиями. Сначала умножить обе части уравнения на t
Затем разделить обе части на 50
Пример 2. Дано буквенное уравнение 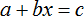
Вычтем из обеих частей уравнения a
Разделим обе части уравнения на b
Теперь, если нам попадется уравнение вида a + bx = c , то у нас будет готовое решение. Достаточно будет подставить в него нужные значения. Те значения, которые будут подставляться вместо букв a, b, c принято называть параметрами. А уравнения вида a + bx = c называют уравнением с параметрами. В зависимости от параметров, корень будет меняться.
Решим уравнение 2 + 4x = 10 . Оно похоже на буквенное уравнение a + bx = c . Вместо того, чтобы выполнять тождественные преобразования, мы можем воспользоваться готовым решением. Сравним оба решения:
Видим, что второе решение намного проще и короче.
Для готового решения необходимо сделать небольшое замечание. Параметр b не должен быть равным нулю (b ≠ 0) , поскольку деление на ноль на допускается.
Пример 3. Дано буквенное уравнение 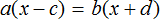
Раскроем скобки в обеих частях уравнения
Воспользуемся переносом слагаемых. Параметры, содержащие переменную x , сгруппируем в левой части уравнения, а параметры свободные от этой переменной — в правой.
В левой части вынесем за скобки множитель x
Разделим обе части на выражение a − b
В левой части числитель и знаменатель можно сократить на a − b . Так окончательно выразится переменная x
Теперь, если нам попадется уравнение вида a(x − c) = b(x + d) , то у нас будет готовое решение. Достаточно будет подставить в него нужные значения.
Допустим нам дано уравнение 4(x − 3) = 2(x + 4) . Оно похоже на уравнение a(x − c) = b(x + d) . Решим его двумя способами: при помощи тождественных преобразований и при помощи готового решения:
Для удобства вытащим из уравнения 4(x − 3) = 2(x + 4) значения параметров a, b, c, d . Это позволит нам не ошибиться при подстановке:
Как и в прошлом примере знаменатель здесь не должен быть равным нулю (a − b ≠ 0) . Если нам встретится уравнение вида a(x − c) = b(x + d) в котором параметры a и b будут одинаковыми, мы сможем не решая его сказать, что у данного уравнения корней нет, поскольку разность одинаковых чисел равна нулю.
Например, уравнение 2(x − 3) = 2(x + 4) является уравнением вида a(x − c) = b(x + d) . В уравнении 2(x − 3) = 2(x + 4) параметры a и b одинаковые. Если мы начнём его решать, то придем к тому, что левая часть не будет равна правой части:
Пример 4. Дано буквенное уравнение 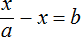
Приведем левую часть уравнения к общему знаменателю:
Умнóжим обе части на a
В левой части x вынесем за скобки
Разделим обе части на выражение (1 − a)
Линейные уравнения с одним неизвестным
Рассмотренные в данном уроке уравнения называют линейными уравнениями первой степени с одним неизвестным.
Если уравнение дано в первой степени, не содержит деления на неизвестное, а также не содержит корней из неизвестного, то его можно назвать линейным. Мы еще не изучали степени и корни, поэтому чтобы не усложнять себе жизнь, слово «линейный» будем понимать как «простой».
Большинство уравнений, решенных в данном уроке, в конечном итоге сводились к простейшему уравнению, в котором нужно было произведение разделить на известный сомножитель. Таковым к примеру является уравнение 2 (x + 3) = 16 . Давайте решим его.
Раскроем скобки в левой части уравнения, получим 2 x + 6 = 16. Перенесем слагаемое 6 в правую часть, изменив знак. Тогда получим 2 x = 16 − 6. Вычислим правую часть, получим 2x = 10. Чтобы найти x , разделим произведение 10 на известный сомножитель 2. Отсюда x = 5.
Уравнение 2 (x + 3) = 16 является линейным. Оно свелось к уравнению 2x = 10 , для нахождения корня которого потребовалось разделить произведение на известный сомножитель. Такое простейшее уравнение называют линейным уравнением первой степени с одним неизвестным в каноническом виде. Слово «канонический» является синонимом слов «простейший» или «нормальный».
Линейное уравнение первой степени с одним неизвестным в каноническом виде называют уравнение вида ax = b.
Полученное нами уравнение 2x = 10 является линейным уравнением первой степени с одним неизвестным в каноническом виде. У этого уравнения первая степень, одно неизвестное, оно не содержит деления на неизвестное и не содержит корней из неизвестного, и представлено оно в каноническом виде, то есть в простейшем виде при котором легко можно определить значение x . Вместо параметров a и b в нашем уравнении содержатся числа 2 и 10. Но подобное уравнение может содержать и другие числа: положительные, отрицательные или равные нулю.
Если в линейном уравнении a = 0 и b = 0 , то уравнение имеет бесконечно много корней. Действительно, если a равно нулю и b равно нулю, то линейное уравнение ax = b примет вид 0x = 0 . При любом значении x левая часть будет равна правой части.
Если в линейном уравнении a = 0 и b ≠ 0 , то уравнение корней не имеет. Действительно, если a равно нулю и b равно какому-нибудь числу, не равному нулю, скажем числу 5, то уравнение ax = b примет вид 0x = 5 . Левая часть будет равна нулю, а правая часть пяти. А ноль не равен пяти.
Если в линейном уравнении a ≠ 0 , и b равно любому числу, то уравнение имеет один корень. Он определяется делением параметра b на параметр a
Действительно, если a равно какому-нибудь числу, не равному нулю, скажем числу 3 , и b равно какому-нибудь числу, скажем числу 6 , то уравнение 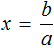
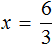
Отсюда 
Существует и другая форма записи линейного уравнения первой степени с одним неизвестным. Выглядит она следующим образом: ax − b = 0 . Это то же самое уравнение, что и ax = b , но параметр b перенесен в левую часть с противоположным знаком. Такие уравнение мы тоже решали в данном уроке. Например, уравнение 7x − 77 = 0 . Уравнение вида ax − b = 0 называют линейным уравнением первой степени с одним неизвестным в общем виде.
В будущем после изучения рациональных выражений, мы рассмотрим такие понятия, как посторонние корни и потеря корней. А пока рассмотренного в данном уроке будет достаточным.
http://ifepoz.ru/kursovye-raboty/oformlenie-formul-trebovaniya-i-primery-v-dissertatsii.html
http://spacemath.xyz/obshhie-svedeniya-ob-uravneniyah/