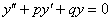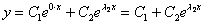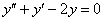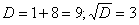Заполните таблицу дифференциальное уравнение характеристическое уравнение

823, 26.03.2020 «Решение дифференциальных уравнений 2-го порядка».

Изучить материал, составить конспект, выполнить задание, фото выполненной работы прислать в ВК.

Просмотр содержимого документа
«823, 26.03.2020 «Решение дифференциальных уравнений 2-го порядка».»

Практическая работа по теме: «Решение дифференциальных уравнений II-го порядка»

Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами

В теории и практике различают два типа таких уравнений – однородное уравнение и неоднородное уравнение.

Однородное ДУ второго порядка с постоянными коэффициентами имеет следующий вид:

, где и – константы (числа), а в правой части – строго ноль.

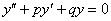
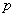
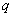
Неоднородное ДУ второго порядка с постоянными коэффициентами имеет вид:
, где и – константы, а – функция, зависящая только от «икс». В простейшем случае функция может быть числом, отличным от нуля.

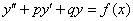
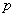
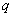
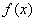
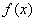
Какая мысль приходит в голову после беглого взгляда? Неоднородное уравнение кажется сложнее. На этот раз первое впечатление не подводит!

Кроме того, чтобы научиться решать неоднородные уравнения необходимо уметь решать однородные уравнения. По этой причине сначала рассмотрим алгоритм решения линейного однородного уравнения второго порядка:

Для того чтобы решить данное ДУ, нужно составить так называемое характеристическое уравнение:

По какому принципу составлено характеристическое уравнение, отчётливо видно:
вместо второй производной записываем ;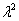
вместо первой производной записываем просто «лямбду»;
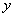
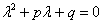
вместо функции ничего не записываем.

– это обычное квадратное уравнение, которое предстоит решить.

Существуют три варианта развития событий.
Они доказаны в курсе математического анализа, и на практике мы будет использовать готовые формулы.

Характеристическое уравнение имеет два различных действительных корня

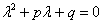
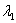
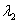
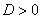
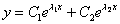
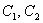
Если характеристическое уравнение имеет два различных действительных корня , (т.е., если дискриминант ), то общее решение однородного уравнения выглядит так:
, где – константы.

В случае если один из корней равен нулю, решение очевидным образом упрощается; пусть, например, 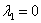, тогда общее решение:

Решить дифференциальное уравнение

Решение: составим и решим характеристическое уравнение:

,

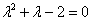
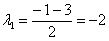
Ответ: общее решение:

Характеристическое уравнение имеет два кратных действительных корня

Если характеристическое уравнение 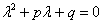имеет два кратных (совпавших) действительных корня (дискриминант ), то общее решение однородного уравнения принимает вид:
, где 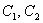– константы.
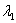
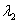
Вместо в формуле можно было нарисовать , корни всё равно одинаковы.

Если оба корня равны нулю , то общее решение опять же упрощается: . Кстати, является общим решением того самого примитивного уравнения , о котором я упоминал в начале урока. Почему? Составим характеристическое уравнение: – действительно, данное уравнение как раз и имеет совпавшие нулевые корни .

Решить дифференциальное уравнение

Решение: составим и решим характеристическое уравнение:

Здесь можно вычислить дискриминант, получить ноль и найти кратные корни. Но можно невозбранно применить известную школьную формулу сокращенного умножения:

Получены два кратных действительных корня

Ответ: общее решение:

Характеристическое уравнение имеет сопряженные комплексные корни

Если характеристическое уравнение 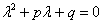имеет сопряженные комплексные корни , (дискриминант ), то общее решение однородного уравнения принимает вид:
, где 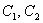– константы.
Примечание: Сопряженные комплексные корни почти всегда записывают кратко следующим образом:

Если получаются чисто мнимые сопряженные комплексные корни: , то общее решение упрощается:

Решить однородное дифференциальное уравнение второго порядка

Решение: Составим и решим характеристическое уравнение:

– получены сопряженные комплексные корни

Ответ: общее решение:

Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям ,

Решение: составим и решим характеристическое уравнение:

,
Получены два различных действительных корня, поэтому общее решение:

Алгоритм нахождения частного решения следующий:

Сначала используем начальное условие :

Согласно начальному условию, получаем первое уравнение: или просто

Далее берём наше общее решение и находим производную:

Используем второе начальное условие :

Согласно второму начальному условию, получаем второе уравнение: или просто

Составим и решим систему из двух найденных уравнений:

Подставим найденные значения констант в общее решение :

Ответ: частное решение:

Найти общее решение дифференциального уравнения 2-го порядка.

Найти частное решение дифференциального уравнения 2-го порядка.

Дифференциальные уравнения высших порядков: ЛОДУ, примеры решения.

Можно выделить 5 возможных метода для определения y₀ — общего решения линейного однородного дифференциального уравнения n-ого порядка с постоянными коэффициентами:

1. В случае, когда все решения характеристического уравнения являются действительными и различными, значит, линейно независимые частные решения принимают вид:

,

а общее решение линейного однородного дифференциального уравнения n-ого порядка с постоянными коэффициентами записывают так:

.

Найти общее решение ЛОДУ 3-го порядка с постоянными коэффициентами:

.

Для начала записываем характеристическое уравнение и находим его корни, перед этим произведя разложение многочлена в левой части равенства на множители методом группировки:

Каждый из трех корней характеристического уравнения являются действительными и различными, значит, общее решение линейного однородного дифференциального уравнения 3-го порядка с постоянными коэффициентами принимает вид:

.

2. Когда каждое решение характеристического уравнения оказывается действительными и одинаковыми, т.е.,

,

значит, линейно независимые частные решения ЛОДУ n-ого порядка с постоянными коэффициентами принимают вид:

,

а общее решение линейного однородного дифференциального уравнения (ДУ) принимает вид:

Найти общее решение ДУ

.

Характеристическое уравнение этого линейного однородного дифференциального уравнения 4-го порядка выглядит так:

.

Обратившись к формуле бинома Ньютона, переписываем характеристическое уравнение как , из чего видим четырехкратный корень k₀ = 2.

Т.о., общим решением заданного ЛОДУ с постоянными коэффициентами является:

.

3. Когда решениями характеристического уравнения ЛОДУ n-ого порядка с постоянными коэффициентами оказываются разные комплексно сопряженные пары , n=2m, тогда линейно независимые частные решения такого линейного однородного дифференциального уравнения принимает вид:

а общее решение записывается так:

Проинтегрировать ЛОДУ 4-го порядка с постоянными коэффициентами .

Характеристическое уравнение этого линейного однородного дифференциального уравнения:

.

Произведя некоторые несложные преобразования и группирования имеем:

Откуда находим 2 пары комплексно сопряженных корней характеристического уравнения и . Тогда, общим решением заданного ЛОДУ n-ого порядка с постоянными коэффициентами является:

4. Когда решениями характеристического уравнения оказываются совпадающие комплексно сопряженные пары , тогда линейно независимые частные решения ЛОДУ n-ого порядка с постоянными коэффициентами выглядят так:

,

а общим решением этого линейного однородного дифференциального уравнения является:

Найти общее решение линейного однородного дифференциального уравнения с постоянными коэффициентами:

.

Первым шагом записываем характеристическое уравнение этого ЛОДУ с постоянными коэффициентами и определяем его корни:

Т.е., решением характеристического уравнения является двукратная комплексно сопряженная пара . Тогда общее решение заданного ЛОДУ с постоянными коэффициентами будет:

.

5. Могут возникнуть любые комбинации случаев, описанных выше, т.е., некоторые корни характеристического уравнения ЛОДУ n-ого порядка с постоянными коэффициентами являются действительными и различными, некоторые являются действительными и совпадающими, некоторые являются различными комплексно сопряженными парами и некоторые совпадающими комплексно сопряженными парами.

Найти общее решение ДУ

.

Характеристическое уравнение этого ЛОДУ с постоянными коэффициентами выглядит так:

.

Многочлен в левой части равенства можно разложить на множители. Из делителей свободного члена вычисляем двукратный корень k₁=k₂=2 и корень k₃=-3. Далее, применяя схему Горнера, приходим к разложению:

.

Из квадратного уравнения находим оставшиеся корни .

Т.о., общее решение заданного ЛОДУ с постоянными коэффициентами выглядит как:

.

Практическая работа по математике на тему: «Дифференциальные уравнения»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Практическая работа № 5.

Тема : Решение дифференциальных уравнений I -го и II -го порядка .

Цель : Проверить на практике знание понятия дифференциального уравнения, виды дифференциальных уравнений, умение решать дифференциальные уравнения I и II –го порядков, находить общее и частное решение.
Обеспечение практической работы :
Теоретический материал методической рекомендации к практической работе.

Практические задания по вариантам.

Теоретический материал и примеры решения дифференциальных уравнений.

1. Дифференциальное уравнение первого порядка, содержит:
1) независимую переменную ;
2) зависимую переменную (функцию);
3) первую производную функции: .

Решить дифференциальное уравнение – это значит, найти множество функций , которые удовлетворяют данному уравнению. Такое множество функций называется общим решением дифференциального уравнения.

Решить дифференциальное уравнение

.

В рассматриваемом примере переменные легко разделяются перекидыванием множителей по правилу пропорции:

Переменные разделены. В левой части – только «игреки», в правой части – только «иксы».

Следующий этап – интегрирование дифференциального уравнения. Интегрируем обе части:

Решение дифференциального уравнения в неявном виде называется общим интегралом дифференциального уравнения. То есть, – это общий интеграл.

Вместо записи обычно пишут .

В данном случае:

Функция представлена в явном виде. Это и есть общее решение.

Множество функций является общим решением дифференциального уравнения .

Придавая константе различные значения, можно получить бесконечно много частных решений дифференциального уравнения.

Найти частное решение дифференциального уравнения , удовлетворяющее начальному условию

По условию требуется найти частное решение ДУ, удовлетворяющее начальному условию. Такая постановка вопроса также называется задачей Коши.

Сначала находим общее решение.

Интегрируем уравнение:

Итак, общее решение: . На завершающем этапе нужно найти частное решение, удовлетворяющее заданному начальному условию .

Необходимо подобрать такое значение константы , чтобы выполнялось заданное начальное условие .

В общее решение вместо «икса» подставляем ноль, а вместо «игрека» двойку:

В общее решение подставляем найденное значение константы :
– это и есть нужное нам частное решение.

Решить дифференциальное уравнение

Решение: Переписываем производную в нужном нам виде:

Переносим второе слагаемое в правую часть со сменой знака:

Переменные разделены, интегрируем обе части:

Решение распишу очень подробно:

Ответ: общий интеграл:

Примечание: общий интеграл любого уравнения можно записать не единственным способом. Таким образом, если у вас не совпал результат с заранее известным ответом, то это еще не значит, что вы неправильно решили уравнение.

Найти частное решение дифференциального уравнения , удовлетворяющее начальному условию . Выполнить проверку.

Решение: Сначала найдем общее решение. Данное уравнение уже содержит готовые дифференциалы и , а значит, решение упрощается. Разделяем переменные:

Интегрируем уравнение:

общее решение:

Найдем частное решение, соответствующее заданному начальному условию

Подставляем найденное значение константы в общее решение.

Ответ: частное решение:

2.Линейные дифференциальные уравнения второго порядка
с постоянными коэффициентами

В теории и практике различают два типа таких уравнений – однородное уравнение и неоднородное уравнение.

Однородное ДУ второго порядка с постоянными коэффициентами имеет следующий вид:

, где и – константы (числа), а в правой части – строго ноль.

Неоднородное ДУ второго порядка с постоянными коэффициентами и меет вид:
, где и – константы, а – функция, зависящая только от «икс» . В простейшем случае функция может быть числом, отличным от нуля .

Какая мысль приходит в голову после беглого взгляда? Неоднородное уравнение кажется сложнее. На этот раз первое впечатление не подводит!

Кроме того, чтобы научиться решать неоднородные уравнения необходимо уметь решать однородные уравнения. По этой причине сначала рассмотрим алгоритм решения линейного однородного уравнения второго порядка:

Для того чтобы решить данное ДУ, нужно составить так называемое характеристическое уравнение:

По какому принципу составлено характеристическое уравнение, отчётливо видно:
вместо второй производной записываем ;
вместо первой производной записываем просто «лямбду»;
вместо функции ничего не записываем.

– это обычное квадратное уравнение, которое предстоит решить.

Существуют три варианта развития событий.
Они доказаны в курсе математического анализа, и на практике мы будет использовать готовые формулы.

Характеристическое уравнение имеет два различных действительных корня

Если характеристическое уравнение имеет два различных действительных корня , (т.е., если дискриминант ), то общее решение однородного уравнения выглядит так:
, где – константы.

В случае если один из корней равен нулю, решение очевидным образом упрощается; пусть, например, , тогда общее решение:

Решить дифференциальное уравнение

Решение: составим и решим характеристическое уравнение:

,

Ответ: общее решение:

Характеристическое уравнение имеет два кратных действительных корня

Если характеристическое уравнение имеет два кратных (совпавших) действительных корня (дискриминант ), то общее решение однородного уравнения принимает вид:
, где – константы.
Вместо в формуле можно было нарисовать , корни всё равно одинаковы.

Если оба корня равны нулю , то общее решение опять же упрощается: . Кстати, является общим решением того самого примитивного уравнения , о котором я упоминал в начале урока. Почему? Составим характеристическое уравнение: – действительно, данное уравнение как раз и имеет совпавшие нулевые корни .

Решить дифференциальное уравнение

Решение: составим и решим характеристическое уравнение:

Здесь можно вычислить дискриминант, получить ноль и найти кратные корни. Но можно невозбранно применить известную школьную формулу сокращенного умножения:

Получены два кратных действительных корня

Ответ: общее решение:

Характеристическое уравнение имеет сопряженные комплексные корни

Если характеристическое уравнение имеет сопряженные комплексные корни , (дискриминант ), то общее решение однородного уравнения принимает вид:
, где – константы.
Примечание: Сопряженные комплексные корни почти всегда записывают кратко следующим образом:

Если получаются чисто мнимые сопряженные комплексные корни: , то общее решение упрощается:

Решить однородное дифференциальное уравнение второго порядка

Решение: Составим и решим характеристическое уравнение:


– получены сопряженные комплексные корни

Ответ: общее решение:

Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям ,

Решение: составим и решим характеристическое уравнение:

,
Получены два различных действительных корня, поэтому общее решение:

Алгоритм нахождения частного решения следующий:

Сначала используем начальное условие :

Согласно начальному условию, получаем первое уравнение: или просто

Далее берём наше общее решение и находим производную:

Используем второе начальное условие :

Согласно второму начальному условию, получаем второе уравнение: или просто

Составим и решим систему из двух найденных уравнений:

Подставим найденные значения констант в общее решение :

Ответ: частное решение:

1. Найти общее решение дифференциального уравнения к разделяющимися переменными.

2. Найти частное решение дифференциального уравнения с разделяющимися переменными.

3.Найти решение однородного дифференциального уравнения первого порядка.

4. Найти общее решение дифференциального уравнения 2-го порядка.

5. Найти частное решение дифференциального уравнения 2-го порядка.

1. Найти общее решение дифференциального уравнения c разделяющимися переменными.

2. Найти частное решение дифференциального уравнения с разделяющимися переменными.

3.Найти решение однородного дифференциального уравнения первого порядка.

4. Найти общее решение дифференциального уравнения 2-го порядка.

5. Найти частное решение дифференциального уравнения 2-го порядка.

1. Найти общее решение дифференциального уравнения c разделяющимися переменными.

2. Найти частное решение дифференциального уравнения с разделяющимися переменными.

3.Найти решение однородного дифференциального уравнения первого порядка.

4. Найти общее решение дифференциального уравнения 2-го порядка.

5. Найти частное решение дифференциального уравнения 2-го порядка.

1. Найти общее решение дифференциального уравнения c разделяющимися переменными.

2. Найти частное решение дифференциального уравнения с разделяющимися переменными.

3.Найти решение однородного дифференциального уравнения первого порядка.

4. Найти общее решение дифференциального уравнения 2-го порядка.

5. Найти частное решение дифференциального уравнения 2-го порядка.

1. Найти общее решение дифференциального уравнения к разделяющимися переменными.

2. Найти частное решение дифференциального уравнения с разделяющимися переменными.

3.Найти решение однородного дифференциального уравнения первого порядка.

4. Найти общее решение дифференциального уравнения 2-го порядка.

5. Найти частное решение дифференциального уравнения 2-го порядка.

1. Найти общее решение дифференциального уравнения к разделяющимися переменными.

2. Найти частное решение дифференциального уравнения с разделяющимися переменными.

3.Найти решение однородного дифференциального уравнения первого порядка.

4. Найти общее решение дифференциального уравнения 2-го порядка.

5. Найти частное решение дифференциального уравнения 2-го порядка.

Критерии оценки практической работы обучающихся

Оценка «5» ставится, если:

работа выполнена полностью;

в логических рассуждениях и обосновании решения нет пробелов и ошибок;

в решении нет математических ошибок (возможна одна неточность, описка, не являющаяся следствием незнания или непонимания учебного материала).

Оценка «4» ставится, если:

работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);

допущена одна ошибка или два-три недочета в выкладках, рисунках, чертежах или графиках (если эти виды работы не являлись специальным объектом проверки).

Оценка «3» ставится, если:

допущены более одной ошибки или более двух-трех недочетов в выкладках, чертежах или графиках, но учащийся владеет обязательными умениями по проверяемой теме.

Оценка «2» ставится, если:

допущены существенные ошибки, показавшие, что учащийся не владеет

обязательными умениями по данной теме в полной мере

Оценка «1» ставится, если:

работа показала полное отсутствие у учащегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.