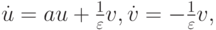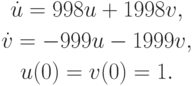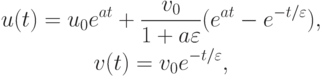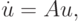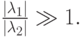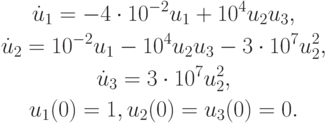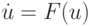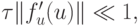Жесткие дифференциальные уравнения что это

Жесткие дифференциальные уравнения что это

В вычислительной практике часто встречаются системы дифференциальных уравнений, которые принято называть жесткими.
Не приводя точного определения жесткой системы, проиллюстрируем содержание этого понятия и возникающие проблемы на примере жесткой линейной системы двух дифференциальных уравнений с постоянными коэффициентами.

Пусть требуется численно решить задачу Коши
y‘₁ = -2y₁ — 998 y₂ ,
y‘₂ = — 1000y₂ ,
y₁ (0) = 2, y₂ (0)=1.
Эту задачу можно записать в матричной форме в виде:

где

искомое решение,

матрица системы,

значение решения в начальной точке x = 0 — начальное условие.

Легко видеть, что точное решение системы имеет вид:
y₁ (x) = exp(-2x) + exp(-1000x),
y₂ (x) = exp(-1000x).
Слагаемое
exp(-1000x)
убывает очень быстро,
а слагаемое exp(-2x) — гораздо медленнее.

Попытаемся найти решение этой задачи методом Рунге-Кутты с различными шагами. Графики полученных решений и графики точного решения приведены ниже (график точного решения — справа).

Видно, что полученные приближенные решения уже на первых шагах содержат большие ошибки. Для получения правдоподобного результата на отрезке [0, 0.1] нужно выбирать шаг, меньший 0.003. Это означает, что для достаточно большого интервала интегрирования потребуется выполнить вычисления для очень большого числа шагов. Казалось бы, можно избежать интегрирования на всем промежутке с малым шагом: вести вычисления с малым шагом до тех пор, пока компонента
exp(-1000x)
станет пренебрежимо малой, а затем увеличить шаг и до конца промежутка интегрирования вести вычисления с большим шагом. Оказывается, что на самом деле это совсем не так. Вторая компонента заставляет вести интегрирование с малым шагом на всем промежутке интегрирования. Это и означает, что система жесткая. Жесткость системы проявляется тогда, когда длина промежутка интегрирования T удовлетворяет соотношению
где l _max — наибольшее по абсолютной величине собственное число матрицы системы A. Для интегрирования жестких систем необходимо применять специально разработанные методы.

ПРИМЕР 1. Интегрирование жесткой системы дифференциальных уравнений.

В примере рассмотрена линейная жесткая система. Однако специальные методы решения жестких систем, как правило, универсальны, т.е. применяются для решения как линейных так и нелинейных систем.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Лекция 10: Численные методы решения жестких систем обыкновенных дифференциальных уравнений

9.1. Явление жесткости. Предварительные сведения

Рассмотрим в качестве примера две задачи Коши для систем обыкновенных дифференциальных уравнений (ОДУ) [9.1], [9.2]:

с начальными данными u(0) = u₀, v(0) = v₀ ; здесь 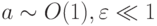; и линейную систему с постоянными коэффициентами

Решением первой задачи Коши являются функции

В обоих случаях решение состоит из двух экспонент: быстро убывающей и относительно медленно изменяющейся. Отметим, что абсолютные величины собственных значений матриц рассматриваемых линейных систем ОДУ при их представлении в виде

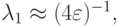
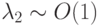
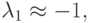
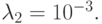
( u — вектор — столбец, A — матрица с постоянными коэффициентами) существенно различаются. Так, в первом случае ; во втором: В обоих случаях имеем:

При моделировании физических процессов причина такой разницы в собственных числах заключена в существенно различных характерных временах процессов, описываемых системами ОДУ. Наиболее часто подобные системы встречаются при моделировании процессов в ядерных реакторах, при решении задач радиофизики, астрофизики, физики плазмы, биофизики, химической кинетики. Последние задачи часто могут быть записаны в виде [9.3]:

где u_k — концентрации веществ, участвующих в химических реакциях, скорости протекания которых характеризуются коэффициентами 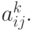В качестве примера приведем одну из систем химической кинетики, описывающую изменение концентрации трех веществ, участвующих в реакции для случая полного перемешивания [9.1].

Пример 1. Обозначим концентрации трех веществ, участвующих в реакции, через u₁ , u₂ и u₃ , тогда

Участки решения, характеризующиеся быстрым и медленным его изменением, называются пограничным слоем и квазистационарным режимом, соответственно.

Трудности численного решения подобных систем ОДУ , получивших название жестких ( определение жесткой системы приведено ниже), связаны с выбором шага интегрирования. Дело в том, что характерные времена исследуемых процессов могут различаться более чем в 10 12 раз. Следовательно, если при численном решении системы

выбирать шаг из условия

то он будет соответствовать самому быстрому процессу. В данном случае затраты машинного времени для исследования самых медленных процессов будут неоправданно велики. По этой причине имеются следующие альтернативы в выборе подхода к численному решению рассматриваемых задач.

1. Численно решать систему ОДУ с шагом

т.е. с учетом характерных времен всех процессов, описываемых данной системой.

Понятие о жестких дифференциальных уравнениях.

, (1.35)

где A = const. Точное решение этого уравнения:

.

Если A —большая положительная величина, то решение задачи (1.35) неустойчиво. Если A —малая величина, то решение задачи (1.35) нейтрально устойчиво. Если A —большая по модулю и отрицательная величина, то каким бы ни было выбрано u₀ через достаточно малый промежуток, называемый переходным участком (или пограничным слоем), кривая решения становится тождественной кривой частного решения p(x) уравнения (1.35). Эта сверхустойчивость решения дифференциальной задачи является идеальной в смысле распространения наследственной ошибки в дифференциальном уравнении, но она создает ряд трудностей численного интегрирования на ЭВМ. Одна из них состоит в том, что хотя решение (1.36) за пределами переходного участка ведет себя как и функция p(x) и практически не зависит от A (при A 6 ).

Это определение “жесткости” системы нам кажется не совсем точным. Действительно, если max Re(-l_i) = 10 -2 , а min Re(-l_i) = 10 -8 , так что их отношение равно 10 6 , то по определению система является “жесткой”. В то же время такая система позволяет из условий устойчивости выбрать шаг интегрирования порядка 100.

Определение, возможно, надо дополнить словами: большие по модулю собственные значения имеют большую отрицательную часть.