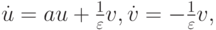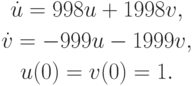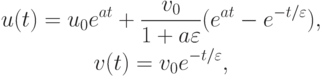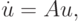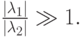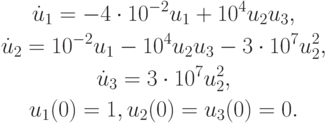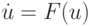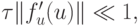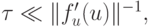Жесткость системы дифференциальных уравнений это

Лекция 10: Численные методы решения жестких систем обыкновенных дифференциальных уравнений

9.1. Явление жесткости. Предварительные сведения

Рассмотрим в качестве примера две задачи Коши для систем обыкновенных дифференциальных уравнений (ОДУ) [9.1], [9.2]:

с начальными данными u(0) = u₀, v(0) = v₀ ; здесь 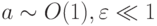; и линейную систему с постоянными коэффициентами

Решением первой задачи Коши являются функции

В обоих случаях решение состоит из двух экспонент: быстро убывающей и относительно медленно изменяющейся. Отметим, что абсолютные величины собственных значений матриц рассматриваемых линейных систем ОДУ при их представлении в виде

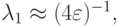
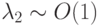
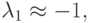
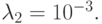
( u — вектор — столбец, A — матрица с постоянными коэффициентами) существенно различаются. Так, в первом случае ; во втором: В обоих случаях имеем:

При моделировании физических процессов причина такой разницы в собственных числах заключена в существенно различных характерных временах процессов, описываемых системами ОДУ. Наиболее часто подобные системы встречаются при моделировании процессов в ядерных реакторах, при решении задач радиофизики, астрофизики, физики плазмы, биофизики, химической кинетики. Последние задачи часто могут быть записаны в виде [9.3]:

где u_k — концентрации веществ, участвующих в химических реакциях, скорости протекания которых характеризуются коэффициентами 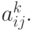В качестве примера приведем одну из систем химической кинетики, описывающую изменение концентрации трех веществ, участвующих в реакции для случая полного перемешивания [9.1].

Пример 1. Обозначим концентрации трех веществ, участвующих в реакции, через u₁ , u₂ и u₃ , тогда

Участки решения, характеризующиеся быстрым и медленным его изменением, называются пограничным слоем и квазистационарным режимом, соответственно.

Трудности численного решения подобных систем ОДУ , получивших название жестких ( определение жесткой системы приведено ниже), связаны с выбором шага интегрирования. Дело в том, что характерные времена исследуемых процессов могут различаться более чем в 10 12 раз. Следовательно, если при численном решении системы

выбирать шаг из условия

то он будет соответствовать самому быстрому процессу. В данном случае затраты машинного времени для исследования самых медленных процессов будут неоправданно велики. По этой причине имеются следующие альтернативы в выборе подхода к численному решению рассматриваемых задач.

1. Численно решать систему ОДУ с шагом

т.е. с учетом характерных времен всех процессов, описываемых данной системой.

Жесткость системы дифференциальных уравнений это

Глава 5. Решение дифференциальных уравнений

5.6 Жесткие системы дифференциальных уравнений

Система дифференциальных уравнений, записанная в матричном виде, Y = A X , считается жесткой, если матрица коэффициентов почти вырожденная. В этом случае решение, возвращаемое функцией rkfixed , может быть неустойчивым. При решении жесткой системы необходимо использовать одну из трех функций, специально разработанных для решения жестких систем дифференциальных уравнений. К ранее существовавшим функциям Stiffb и Stiffr , реализующим методы Булирша – Штера или Розенброка соответственно, в MathCAD 2001 i добавилась функция Radau , реализующая метод RADAU 5. рассмотрим вначале функции Stiffb и Stiffr .

Вид матрицы, возвращаемой этими функциями, совпадает с возвращаемым функцией rkfixed . Однако функции Stiffb и Stiffr требуют дополнительно задания якобиана системы уравнений.

Обращение к этим функциям:

Здесь у – вектор начальных условий размерности m , где m – порядок ОДУ или число уравнений в системе ОДУ; х₁ и х₂ – начало и конец интервала интегрирования, на котором ищется решение системы ОДУ; начальные условия, заданные вектором у, – это значение решения системы в точке х₁; n – число точек (не считая начальной), в которой ищется решение; D ( x , y ) – m – мерный вектор, который содержит первые производные неизвестных функций; J ( x , y ) – функция, которая возвращает матрицу размером . Первый столбец ее содержит производные F ( t , y ) по у. Остальные столбцы представляют собой матрицу Якоби системы ОДУ.

Пример решения жесткой системы ОДУ приведен на рис. 5.14.

Рис. 5. 14 Пример решения жесткой системы ОДУ

Следует заметить, что увеличение числа шагов в 1000 раз позволяет решить приведенную систему с помощью функции rkfixed ( рис. 5.15), но это оттого, что заданная система не слишком жесткая. Если увеличить разницу в коэффициентах уравнений, то функция rkfixed потребует гигантского числа шагов и в принципе не сможет решить систему.

Рис. 5. 15 Решение жесткой системы ОДУ функцией rkfixed

Новая функция Radau , введенная в MathCAD 2001 i , имеет такой же список аргументов, как и функция Rkadapt и Bulstoer , а именно: Radau (у, x ₁ , x ₂ , D ).

Функция Radau предназначена для решения систем жестких ОДУ, как и функции Stiffr и Stiffb . Преимуществом функции Radau перед Stiffr и Stiffb является то, что она требует указания якобиана в качестве параметра функции.

Сравнение результатов расчета жесткой системы ОДУ с помощью функций Radau и Stiffr приведено на рис. 5 . 16 . Численные результаты, естественно, совпадают, но использование функции Radau проще.

Рис. 5. 1 6 Решение жесткой системы уравнений функциями Radau и Stiffr

На рис. 5 . 17 показано решение той же системы ОДУ с использованием функции Odesolve (в контекстном меню выбран способ решения Stiff ).

Given

Рис. 5. 1 7 Решение жесткой системы уравнений функцией Odesolve

Жесткость системы дифференциальных уравнений это

В вычислительной практике часто встречаются системы дифференциальных уравнений, которые принято называть жесткими.
Не приводя точного определения жесткой системы, проиллюстрируем содержание этого понятия и возникающие проблемы на примере жесткой линейной системы двух дифференциальных уравнений с постоянными коэффициентами.

Пусть требуется численно решить задачу Коши
y‘₁ = -2y₁ — 998 y₂ ,
y‘₂ = — 1000y₂ ,
y₁ (0) = 2, y₂ (0)=1.
Эту задачу можно записать в матричной форме в виде:

где

искомое решение,

матрица системы,

значение решения в начальной точке x = 0 — начальное условие.

Легко видеть, что точное решение системы имеет вид:
y₁ (x) = exp(-2x) + exp(-1000x),
y₂ (x) = exp(-1000x).
Слагаемое
exp(-1000x)
убывает очень быстро,
а слагаемое exp(-2x) — гораздо медленнее.

Попытаемся найти решение этой задачи методом Рунге-Кутты с различными шагами. Графики полученных решений и графики точного решения приведены ниже (график точного решения — справа).

Видно, что полученные приближенные решения уже на первых шагах содержат большие ошибки. Для получения правдоподобного результата на отрезке [0, 0.1] нужно выбирать шаг, меньший 0.003. Это означает, что для достаточно большого интервала интегрирования потребуется выполнить вычисления для очень большого числа шагов. Казалось бы, можно избежать интегрирования на всем промежутке с малым шагом: вести вычисления с малым шагом до тех пор, пока компонента
exp(-1000x)
станет пренебрежимо малой, а затем увеличить шаг и до конца промежутка интегрирования вести вычисления с большим шагом. Оказывается, что на самом деле это совсем не так. Вторая компонента заставляет вести интегрирование с малым шагом на всем промежутке интегрирования. Это и означает, что система жесткая. Жесткость системы проявляется тогда, когда длина промежутка интегрирования T удовлетворяет соотношению
где l _max — наибольшее по абсолютной величине собственное число матрицы системы A. Для интегрирования жестких систем необходимо применять специально разработанные методы.

ПРИМЕР 1. Интегрирование жесткой системы дифференциальных уравнений.

В примере рассмотрена линейная жесткая система. Однако специальные методы решения жестких систем, как правило, универсальны, т.е. применяются для решения как линейных так и нелинейных систем.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter