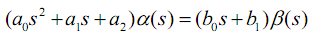Значение дифференциальных уравнений в физике

Значение дифференциальных уравнений в физике

Дифференциальные уравнения в физике. Общие понятия

Многие задачи физики приводят к необходимости решения дифференциальных уравнений. Это обусловлено тем, что практически все физические законы, описывающие физические процессы являются дифференциальными уравнениями, относительно некоторых функций, характеризующих эти процессы. Данные физические законы представляют собой теоретическое обобщение многочисленных экспериментов и описывают эволюцию искомых величин в общем случае, как в пространстве, так и во времени. В частности, второй закон Ньютона, является не чем иным, как дифференциальным уравнением второго порядка:

(1)

и основной задачей динамики является определение закона движения материальной точки по заданным силам , действующим на эту точку, что в математическом отношении означает решение уравнения (1) и определение координат материальной точки как функций времени: .

С учётом сказанного, учитывая важность дифференциальных уравнений для изучения как общей, так и теоретической физики, рассмотрим основные понятия и приёмы интегрирования некоторых видов дифференциальных уравнений, наиболее часто встречающихся в физических приложениях, сопровождая изложение материала конкретными примерами.

Дифференциальным уравнением называется уравнение, которое кроме независимых переменных и неизвестных функций этих переменных, содержит ещё и производные неизвестных функций.

Если функции, входящие в дифференциальное уравнение зависят от одной независимой переменной, то уравнение называется обыкновенным дифференциальным уравнением.

Если же в уравнение входят частные производные неизвестных функций по нескольким независимым переменным, то уравнение называют дифференциальным уравнением с частными производными.

Наивысший порядок производных неизвестной функции, входящих в дифференциальное уравнение называется порядком дифференциального уравнения.

Мы будем рассматривать лишь обыкновенные дифференциальные уравнения. При этом, поскольку при описании динамики физических процессов, все величины, характеризующие эти процессы, зависят от времени, то при изложении материала, независимое переменное обозначим через t .

Классическая механика: о диффурах «на пальцах»

Введение

В этой статье я продолжаю тему цифровой обработки сигналов. В ней я постараюсь простым языком рассказать о концепции игровой механики (физики) с использованием подхода на основе дифференциальных уравнений. В будущем я собираюсь оценить действительно ли реализация такого подхода приведет к резкому увеличению вычислительной нагрузки. В рамках этой статьи не получится — слишком большой объем. В этой я собираюсь описать назначение коэффициентов, входящих в математическую модель динамического объекта, описать их физический смысл, т.е. их влияние на поведение динамического объекта.
Начнем пожалуй…

Физический смысл

В своей статье про Фильтр Калмана я описал что такое уравнения вида «вход-выход», передаточная функция и операторная форма записи дифференциальных уравнений (см. раздел «Основные понятия» в [2]). Примером части математической модели динамического объекта в операторной форме записи может служить следующее уравнение:
(1)
Это распространенная упрощенная модель динамических систем. Опережая напишу, что модель тела в движке «Farseer» использует урезанный аналог представленной выше модели (динамического звена второго порядка). Ниже представлено описание принятых в ней обозначений.

• а0, а1, а2 — коэффициенты инерции, демпфирования и жесткости, соответственно.
• b0, b1 — коэффициенты входного воздействия.
• s — оператор Лапласса (d/dt).
• α(s), β(s) — выходная и входная переменные, как функции оператора Лапласса.

Представленное уравнение описывает динамическую систему типа «один вход — один выход» (SISO). Ее можно использовать для описания динамики объекта по одной из его степеней свободы. Как Вам, возможно, известно, у свободного тела есть шесть степеней свободы — три поступательные (линейное движение вдоль трех осей системы координат (СК) ) и три вращательные (повороты вокруг осей СК). Таким образом, полная модель физического тела будет описываться шестью такими уравнениями (или четырьмя для 2D случая). Вы сразу можете сказать, что уже это свидетельствует о слишком высокой сложности такого подхода. Но на самом деле в Farseer, к примеру, класс тела (Body) содержит и линейные координаты тела (по сути это пара α(s) по OX и OY), и линейные скорости (пара s*α(s) по OX и OY) и параметры ориентации и угловой скорости. Эти параметры обсчитываются раздельно для каждой из осей, т.е. количество уравнений такое же — два уравнения по оси OX (линейное и угловое движение) и два для оси OY. Разница лишь в форме уравнений.
Алгоритм в движке Farseer — приближенный и упрощенный, но позволяет работать с варьируемыми квантами времени. В функцию обсчета параметров движения (Island.Solve(ref TimeStep step, ref Vector2 gravity)) передается время, прошедшее после последнего обсчета параметров. Это позволяет при недостаточной производительности компьютера держать скорость течения игрового времени примерно постоянным в ущерб плавности и реалистичности движения игровых объектов.
При построении дискретной модели на основе диференциальных уравнений мы четко завязываемся на фиксированный квант времени. Уравнения интегрируются для изначально заданной частоты дискретезации, и если с момента последнего обсчета по какой-то причине прошло времени больше, чем заданный квант (в англоязычной литературе его называют «time sample»), то мы либо должны произвести обсчет несколько раз, либо получим замедление движения объекта. Последнее я как раз и наблюдал в игре «Command Cortex» на слабой машине. Движения акторов были плавными но медленными (акторы, управляемые человеком, получают преимущество). Таким образом, нельзя говорить об исключительном преимуществе одного из этих подходов.
Теперь о том, за что отвечают коэффициенты представленного выше уравнения. Это уравнение описывает движение физического тела относительно положения равновесия при α(s) = 0. Это еще одна из причин кажущегося неудобства применения такой модели в игровой механике. При отсутствии приложенных внешних сил данная модель рано или поздно возвратит (при условии устойчивости модели) тело в положение равновесия. Представьте игровой мир, наполненный шариками, которые все время стремятся в начало координат (например, в левый верхний угол экрана). К такому поведению приводит наличие коэффициента жесткости (см. а2 выше). Представьте, что тело соединено с началом координат пружиной. Пока на тело действуют силы, пружина растянута, но стоит убрать внешнее воздействие и тело устремится к нулю. Тела в движке Farseer таким поведением не обладают. Если мы зададим коэффициент a2 равным нулю, то и в данном случае тела не будут стремиться к началу координат (см. выше я писал, что модели в Farseer по сути урезанные варианты этой модели). Ну и зачем этот коэффициент тогда нужен, спросите Вы. Если раскрыть скобки в левой части уравнения (1) и вместо слагаемого
a2*α(s)
напишем
a2*(α(s) — α0)
то через α0 мы получим возможность задать положение, к которому игровой объект будет стремиться. Величина коэффициента а2 отвечает за то, насколько быстро тело переместится в заданное положение равновесия (чем больше значение, тем выше жесткость пружины). Как такое реализовывается в Farseer я пока не выяснил, но думаю придется создать дополнительный источник воздействия.
Теперь коэффициент a1. Это коэффициент демпфирования. Чем больше значение этого коэффициента, тем быстрее гасится скорость (линейная или угловая). Аналогия из жизни — вязкие жидкости, такие как масло, мед, эпоксидная смола. Эти жидкости очень вязкие (имеют большое значение коэффициента демпфирования). Чем выше скорость движения тела в них, тем выше сопротивление этому движения. Если медленно двигать в них ложку, например, то преодолеть сопротивление большого труда не составит, а вот если ударить с размаху, то удар будет жестким.
Величина коэффициента а0 характеризует инерцию объекта. При описании линейного движения в качестве коэффициента а0 используется масса. Чем выше его значение, тем медленнее тело набирает скорость при приложении к нему внешних сил.
Теперь о коэффициентах в правой части уравнения (1). Тут нужно заметить, что данная модель расширенная на случай, когда входное воздействие определяется не только самим значением внешней силы, но и ее изменением. Для описания динамики игровых объектов это, возможно, будет излишним. Однако в промышленных системах управление встречаются и такие модели. Каков же их физический смысл? Коэффициент b1 это по сути коэффициент передачи внешней силы вовнутрь объекта. Обычно он равен еденице, т.е. сила передается как есть.
Коэффициент b0 интересен. Он играет роль форсирующего коэффициента. Представьте очень инерционный объект, к которому прикладывают силу, плавно нарастающую со временем. Если скорость нарастания и конечная величина силы будут малы, то объект очень медленно набирать скорость. Но если силу сделать большой, то после достижения внешней силой заданного значения объект не остановится в каком-то положении, а будет колебаться под действием инерции. Форсирование — это воздействие, пропорциональное скорости нарастания внешней силы. Если мы выберем его большим, то даже при малой скорости нарастания внешней силы наш объект будет достаточно быстро набирать скорость, а когда внешняя сила достигнет заданного значения, форсирование отключится. Вот такой вот хитрый этот «b0».

Динамика в картинках

Чтобы наглядно показать влияние коэффициентов дифф. уравнения на поведение динамического объекта решил построить графики переходного процесса при ступенчатом (step response) и импульсном (impulse response) входных воздействиях. Всего представлено 6 групп графиков (по одной группе для каждого коэффициента). Графики построены в пакете Octave (v. 3.4) с установленным пакетом «Signal Processing».
Итак, в качестве исходной возьмем модель вида:
=========================================
>>> w = tf([1 1],[1 1 1])

Transfer function «w» from input «u1» to output…

y1: (s + 1)/(s^2 + s + 1)

Continuous-time model.
=========================================


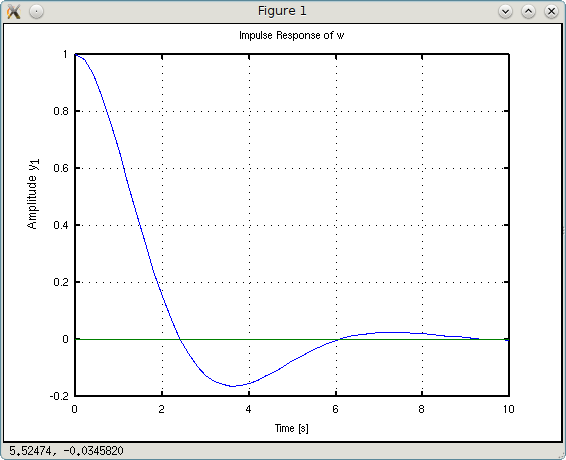
Код «w = tf([1 1],[1 1 1])» в символьном виде имеет вид:
>>> w = tf([b0 b1],[a0 a1 a2])
На скриншотах внизу-справа — примерное время стабилизации (коридором стабильности считаем ± 5% от заданной величины).

Попробуем поиграться с коэффициентом жесткости a2.
>>> w1 = 0.1*tf([1 1],[1 1 0.1])
y1: (s + 1)/(s^2 + s + 0.1)

>>> w2 = 10*tf([1 1],[1 1 10])
y1: (s + 1)/(s^2 + s + 10)
Примечание: пришлось подшаманить с коэффициентами усиления, чтобы результирующий коэффициент усиления был равен единице.


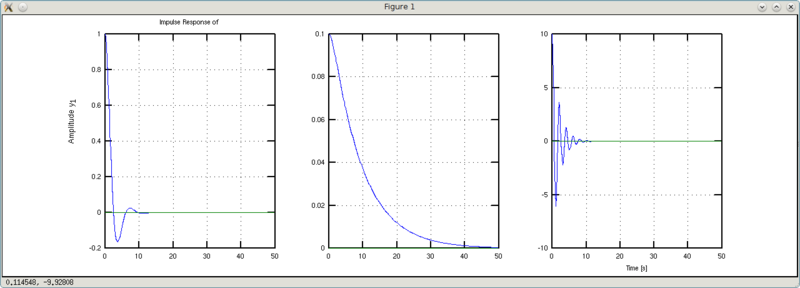
Что видно на графиках? Слева-направо представлены графики для w, w1 и w2, соответственно. Графики w1 более плавные и медленнее достигают установившегося значения. Графики w2 имеют более колебательный характер, но быстрее достигают установившегося значения. Вывод: жестче пружина — больше колебаний, но короче переходный процесс.

Попробуем поиграться с демпфированием (а1).
>>> w1 = tf([1 1],[1 0.25 1])
y1: (s + 1)/(s^2 + 0.25s + 1)

>>> w2 = tf([1 1],[1 2 1])
y1: (s + 1)/(s^2 + 2s + 1)


Сразу вывод: больше вязкость — быстрее затухают колебания.

Попробуем поиграться с инерцией (а0).
>>> w1 = tf([1 1],[0.1 1 1])
y1: (s + 1)/(0.1s^2 + s + 1)

>>> w2 = tf([1 1],[2 1 1])
y1: (s + 1)/(2s^2 + s + 1)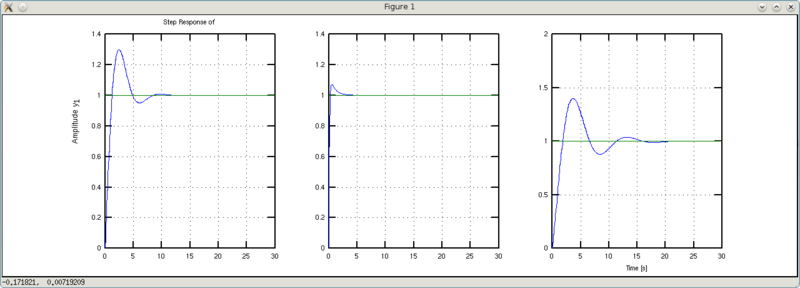


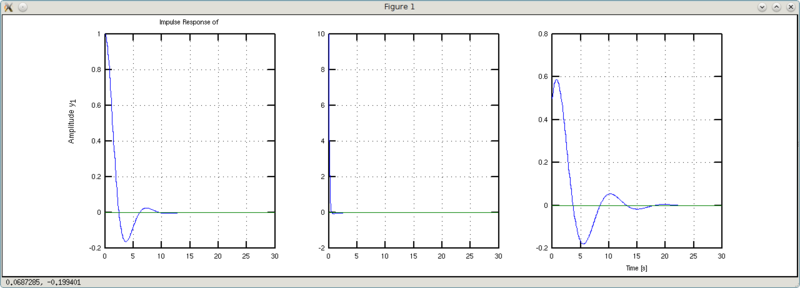
Вывод: меньше масса чугуняки — меньше болтанки и короче переходный процесс.

Перейдем к правой части и поиграемся с b1.
>>> w1 = 10*tf([1 0.1],[1 1 1])
y1: (10 s + 1)/(s^2 + s + 1)

>>> w2 = 0.25*tf([1 4],[1 1 1])
y1: (0.25 s + 1)/(s^2 + s + 1)


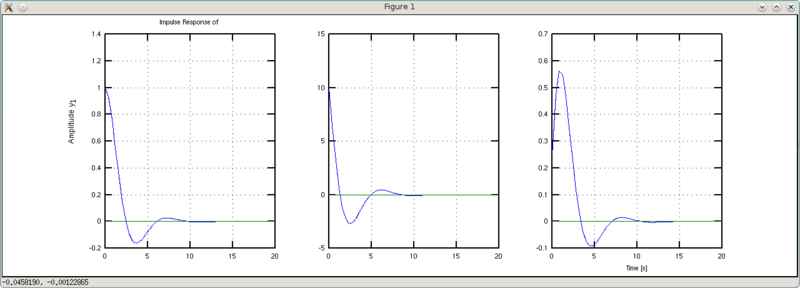
Вроде бы разница еле заметна, если смотреть на графики Step Response. Но на графиках Impulse Response хорошо виден эффект этого коэффициента. Если он равен единице, то график импульсного переходного процесса начинается с единицы (на самом деле он выходит из нуля, но не суть важно — второе значение в графике еденица). График w1 «начинается» со значения 10 (обратная величина от 0.1), а график w2 — начинается со значения 0.25 (обратное к 4). Таким образом, коэффициент b1 можно «обозвать» коэффициентом эффективности управления (входного воздействия).

И напоследок вкусненькое — игры с коэффициентом b0. Это хитрый коэффициент, потому и сравнение будет не таким как было выше. Чтобы показать его эффект придется варьровать несколько коэффициентов.
>>> w1 = tf([6 1],[1 1 1])
y1: (6 s + 1)/(s^2 + s + 1)

>>> w2 = tf([6 1],[1 3 1])
y1: (6 s + 1)/(s^2 + 3 s + 1)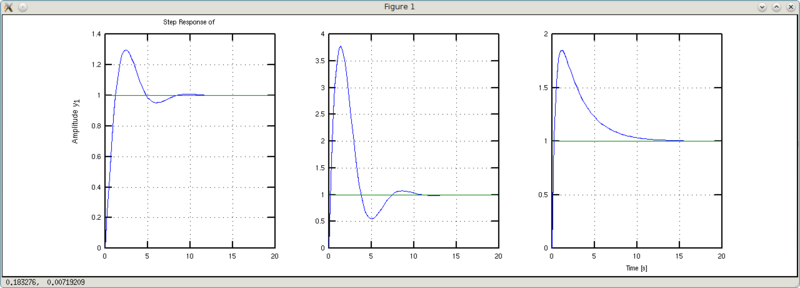


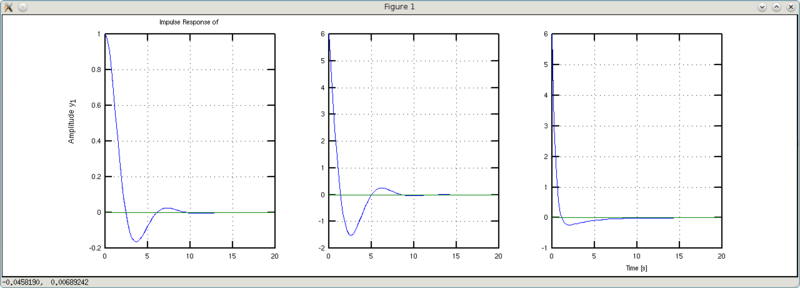
Чем отличаются друг от друга w1 и w2? У w2 в три раза больше коэффициент демпфирования. В результате получаем интересные выводы. Графики w1 и w2 раньше пересекают уровень установившегося значения чем дефолтный график. Однако график w1 сохраняет форму дефолтного с его колебательностью, а график w2 за счет увеличенного демпфирования более сглаженный. Таким образом, играясь с форсированием и демпфированием мы можем заставить даже чугунный утюг порхать по рингу как бабочка без колебаний туда-сюда.

На правах PS

В данной статье я рассматривал лишь положительные значения коэффициентов. Их положительность — необходимое условие устойчивости мат. модели. Однако можно попробовать поиграться и с отрицательными значениями. Неустойчивой системой также можно управлять. Вспомните о самолетах пятого поколения (например, наш Беркут). Обратная стреловидность крыла — это неустойчивый планер, но зато высокая маневренность. Автоматика способна скорректировать эту неустойчивость и при этом, когда нужно, закладывать крутые виражи.
Если получится, состряпаю игрушку, с которой можно будет наглядно увидеть все эти эффекты.

Конспект урока по теме: «Дифференциальные уравнения в физике.»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Конспект урока алгебры и начала анализа в 11 классе

Тема урока: Дифференциальные уравнения в физике.

Цель урока: Создать условия для систематизации расширения углубленных знаний и умений учащихся по данной теме.

закрепить полученные знания;

расширить понятие о дифференциальных уравнениях.

развитие у обучающихся умений сопоставлять, анализировать, выделять главное, обобщать, формулировать выводы;

развитие пространственного воображения.

воспитание познавательной активности, умений самостоятельно добывать знания;

формирование культуры общения.

Тип урока : закрепление изученного материала.

знание дифференциальных уравнений;

знание методики решения дифференциальных уравнений;

умение составлять и решать дифференциальные уравнения.

способность принимать и сохранять цели и задачи учебной деятельности, находить способы её осуществления;

умение планировать, контролировать и оценивать учебные действия в соответствии с поставленной задачей и условиями её выполнения;

умение включаться в диалог с учителем и сверстниками, в коллективное обсуждение проблем;

умение оценивать себя и результаты своей работы.

Колягин, Ю.М. Алгебра и начала математического анализа. 11 класс: учеб. для учащихся общеобразоват. учреждений (профильный уровень) [Текст]/ Ю.М. Колягин, Ю.В. Сидоров, М.В. Ткачева и др. – 8-е изд., стер. -М.: Мнемозина, 2010. – 94 с.

Приветствие учеников, проверка посещаемости, проверка готовности классной комнаты и учащихся к уроку.

Актуализация опорных знаний

Проверка домашнего задания, решить задачи,

которые вызвали затруднения.

Решить дифференциальные уравнения

Постановка темы и цели урока

Учитель: Изучая различные физические явления, в первую очередь, создают его математическую идеализацию или, иными словами, математическую модель, то есть, отбрасывая второстепенные характеристики явления, так же записывают основные законы, управляющие этим явлением, в математической форме. Почти всегда эти законы можно записать в виде дифференциальных уравнений. К примеру, модели различных явлений механики непрерывной среды, химических реакций, электрических и магнитных явлений и др.

Учитель: Можете назвать тему нашего урока? И какая цель урока?

Учащиеся: Дифференциальные уравнения в физике. Расширить свои знания, уметь составлять дифференциальные уравнения по условию физической задачи и решать эти уравнения.

2.1. Первичное закрепление в измененной ситуации

Составим дифференциальное уравнение для гармонического колебания. Учитель на доске записывает решение, ученики в тетрадях.

Задача 1. В практике часто встречаются процессы, которые периодически повторяются, например колебательные движения маятника, струны, пружины и т.д.; процессы, связанные с переменным электрическим током, магнитным полем и т.п. Решение многих таких задач сводится к решению дифференциального уравнения

где заданное положительное число.

Решениями уравнения (1) являются функции

где постоянные, определяемые условиями конкретной задачи. Уравнение (1) называют дифференциальным уравнением гармонических колебаний, а равенство (2) называют уравнением гармонических колебаний.

Например, если отклонение точки свободно колеблющейся струны от положения равновесия в момент времени то

где амплитуда колебания, частота, начальная фаза. Графиком гармонического колебания является синусоида.

Задача 2 (о радиоактивном распаде). Эксперименты показывают, что скорость распада радиоактивного вещества пропорциональна имеющемуся количеству этого вещества.

Следовательно, если масса вещества в момент времени , то

где положительная постоянная.

Знак «-» в уравнении (3) обусловлен тем, что ,а , так как с течением времени количество вещества уменьшается.

Как и для уравнения проверяется, что функции

являются решениями уравнения (3).

Если задано начальное условие

то из равенств (4) и (5) имеем . Следовательно, функция

Является решением дифференциального уравнения (3) при начальном условии (5).

Заметим, что на практике скорость распада радиоактивного вещества характеризуется периодом полураспада, т.е. промежутком времени, в течение которого распадается половина исходного вещества.

Пусть период полураспада, тогда из равенства (6) при находим откуда

Подставляя найденное значение в формулу (20), получаем

В частности, если то .

2.2. Творческое применение и добывание знаний в новой ситуации

Задача 4. На вертикальной пружине закреплён груз массой . Груз выводят из положения равновесия в вертикальном направлении и потом отпускают. Найти закон движения груза, пренебрегая массой пружины и сопротивлением воздуха.

Решение. Направим ось О X вниз по вертикальной прямой, проходящей через точку подвеса груза, которую и примем за начало координат.

Составим дифференциальное уравнение, опираясь на II закон Ньютона:

здесь – масса груза, – ускорение движения, – результирующая всех сил, приложенных к телу.

В положении равновесия сила тяжести, проекция которой на ось О X равна , уравнивается упругой силой пружины, которая согласно закону Гука пропорциональна удлинению пружины:

здесь ω* — коэффициент жёсткости пружины.

Обозначим через отклонение груза от положения равновесия. В момент времени на тело будут действовать две силы: сила тяжести , тянущая груз вниз, и упругая сила пружины, равная и направленная вверх.

Результирующая сила будет равна:

На основании закона Ньютона получаем:

В случае прямолинейного движения вдоль оси О X ускорение равно . Равенство можно записать в виде , откуда

Получили дифференциальное уравнение движения тела – линейное однородное уравнение второго порядка с постоянными коэффициентами.

Корнями его характеристического уравнения являются комплексные числа , поэтому общее решение уравнения

Для выяснения физического смысла полученного решения преобразуем его:

Тогда общее решение уравнения запишется так:

где и – новые произвольные постоянные.

Величина называется амплитудой колебания, аргумент – фазой колебания, его значение при – начальной фазой, – частотой колебания.

Пусть в начальный момент времени отклонение груза от положения равновесия равно , а скорость движения , т.е. , По этим начальным условиям можно найти амплитуду и начальную фазу.

В силу условий при , учитывая равенство получаем:, откуда

Подставив найденные значения и получим:

Формула выражает закон движения груза. Из неё видно, что груз совершает гармонические колебания около положения равновесия.

Частота и период колебания соответственно равны:

Как видно, частота и период колебания зависят только от жёсткости пружины и массы груза, т. е. определяются свойствами самой системы.

Амплитуда же колебаний и начальная фаза зависят также от начальных условий .

Задача 5. В замкнутую электрическую цепь последовательно включены источник тока с электродвижущей силой (ЭДС) , меняющейся с течением времени, активное сопротивление и катушка с индуктивностью . Выведем закон изменения силы тока с течением времени, если вначале (при ) она равнялась нулю.

Решение. Из курса физики знаем, что , где – напряжение на активном участке цепи, выражаемое по закону Ома , а пропорционально скорости изменения силы тока с коэффициентом пропорциональности , . Тогда имеет место равенство

Мы получили дифференциальное уравнение для силы тока с начальным условием .

Данное уравнение является линейным ( и входят в него в первых степенях). Решая его, находим:

Разберем два частных случая:

Электродвижущая сила постоянна, . В этом случае имеем:

В силу начального условия , т.е. откуда получим: и потому

При получаем, что , т.е. после включения постоянной электродвижущей силы значение возрастает от нуля до значения , даваемого законом Ома.

Электродвижущая сила периодически изменяется по синусоидальному закону: . В этом случае имеем:

Вычисляя интеграл, получаем, что

Из начального условия находим, что и потому

С течением времени при второе слагаемое стремится к нулю, и мы получаем, что

то это равенство можно записать в виде

Иными словами, синусоидальные колебания ЭДС дают в пределе синусоидальные колебания силы тока (со сдвигом фазы)

Подведение итога урока.

Учитель: Зачем нужны дифференциальные уравнения в физике? Нужны ли вообще дифференциальные уравнения?

Учащиеся: отвечают на поставленные вопросы. Обсуждают результаты урока.

Учащиеся устно должны закончить предложение:

На сегодняшнем уроке я понял, я узнал, я разобрался…

Я похвалил бы себя…

Особенно мне понравилось…

Сегодня мне удалось…

Я почувствовал, что…

Информация о выполнении домашнего задания.

Дома самостоятельно рассмотреть задачи 3*-4*, на стр. 95-96.

3.4.Оценка содержательного аспекта деятельности обучающихся на уроке.

Учитель выставляет оценки за урок, комментируя ошибки и недочеты.