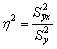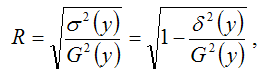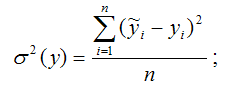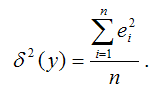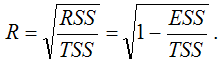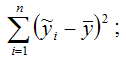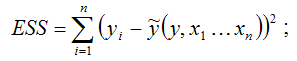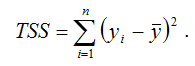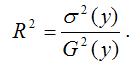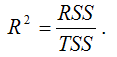Пример нахождения коэффициента детерминации
Коэффициент детерминации рассчитывается для оценки качества подбора уравнения регрессии. Для приемлемых моделей предполагается, что коэффициент детерминации должен быть хотя бы не меньше 50%. Модели с коэффициентом детерминации выше 80% можно признать достаточно хорошими. Значение коэффициента детерминации R 2 = 1 означает функциональную зависимость между переменными.
Для линейной зависимости коэффициент детерминации равен квадрату коэффициента корреляции rxy: R 2 = rxy 2 .
2 «>Рассчитать свое значение
Например, значение R 2 = 0.83, означает, что в 83% случаев изменения х приводят к изменению y . Другими словами, точность подбора уравнения регрессии — высокая.
В общем случае, коэффициент детерминации находится по формуле: 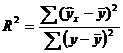
В этой формуле указаны дисперсии: 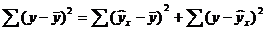
где ∑(y- y ) 2 — общая сумма квадратов отклонений;
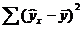
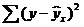
В случае нелинейной регрессии коэффициент детерминации рассчитывается через этот калькулятор. При множественной регрессии, коэффициент детемрминации можно найти через сервис Множественная регрессия
Пример . Дано:
- доля денежных доходов, направленных на прирост сбережений во вкладах, займах, сертификатах и в покупку валюты, в общей сумме среднедушевого денежного дохода, % (Y)
- среднемесячная начисленная заработная плата, тыс. руб. (X)
Следует выполнить: 1. построить поле корреляции и сформировать гипотезу о возможной форме и направлении связи; 2. рассчитать параметры уравнений линейной и A1; 3. выполнить расчет прогнозного значения результата, предполагая, что прогнозные значения факторов составят B2 % от их среднего уровня; 4. оценить тесноту связи с помощью показателей корреляции и детерминации, проанализировать их значения; 5. Дать с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом; 6. Оценить с помощью средней ошибки аппроксимации качество уравнений; 7. Оценить надежность уравнений в целом через F-критерий Фишера для уровня значимости а = 0,05. По значениям характеристик, рассчитанных в пп. 5,6 и данном пункте, выберете лучшее уравнение регрессии и дайте его обоснование.
- Решение онлайн
- Видео решение
Уравнение имеет вид y = ax + b
1. Параметры уравнения регрессии.
Средние значения
Связь между признаком Y фактором X сильная и прямая.
Уравнение регрессии
Коэффициент детерминации для линейной регрессии равен квадрату коэффициента корреляции.
R 2 = 0.91 2 = 0.83, т.е. в 83% случаев изменения х приводят к изменению y. Другими словами — точность подбора уравнения регрессии — высокая
| x | y | x 2 | y 2 | x ∙ y | y(x) | (y-y cp ) 2 | (y-y(x)) 2 | (x-x p ) 2 |
| 15.1 | 255 | 228.01 | 65025 | 3850.5 | 505.26 | 527451.17 | 62630.22 | 420.25 |
| 17 | 261 | 289 | 68121 | 4437 | 549.38 | 518772.07 | 83161.41 | 345.96 |
| 12 | 293 | 144 | 85849 | 3516 | 433.28 | 473699.53 | 19678.51 | 556.96 |
| 10 | 310 | 100 | 96100 | 3100 | 386.84 | 450587.75 | 5904.58 | 655.36 |
| 74 | 1425 | 5476 | 2030625 | 105450 | 1872.88 | 196906.67 | 200600 | 1474.56 |
| 83 | 1985 | 6889 | 3940225 | 164755 | 2081.86 | 1007497.33 | 9381.6 | 2246.76 |
| 85 | 2549 | 7225 | 6497401 | 216665 | 2128.3 | 2457813.93 | 176990.6 | 2440.36 |
| 81 | 2012 | 6561 | 4048144 | 162972 | 2035.42 | 1062428.38 | 548.49 | 2061.16 |
| 22 | 1562 | 484 | 2439844 | 34364 | 665.47 | 337260.88 | 803758.38 | 184.96 |
| 10 | 386 | 100 | 148996 | 3860 | 386.84 | 354332.48 | 0.71 | 655.36 |
| 4 | 383 | 16 | 146689 | 1532 | 247.52 | 357913.03 | 18353.53 | 998.56 |
| 14.1 | 354.1 | 198.81 | 125386.81 | 4992.81 | 482.04 | 393327.58 | 16368.87 | 462.25 |
| 427.2 | 11775.1 | 27710.82 | 19692405.81 | 709494.31 | 11775.1 | 8137990.81 | 1397376.9 | 12502.5 |
Значимость коэффициента корреляции
По таблице Стьюдента находим Tтабл
Tтабл (n-m-1;a) = (10;0.05) = 1.812
Поскольку Tнабл > Tтабл , то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициента корреляции статистически — значим
Анализ точности определения оценок коэффициентов регрессии
S a = 3.3432
Доверительные интервалы для зависимой переменной
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X = 1
(-557.64;913.38)
Проверка гипотез относительно коэффициентов линейного уравнения регрессии
1) t-статистика
Статистическая значимость коэффициента регрессии a подтверждается (6.95>1.812).
Статистическая значимость коэффициента регрессии b не подтверждается (0.96 Fkp, то коэффициент детерминации статистически значим
Показатели корреляции и детерминации для нелинейных моделей регрессии
Индексом корреляции для нелинейных форм связи называется коэффициент корреляции, который вычисляется для оценки качества построенной нелинейной модели регрессии.
Индекс корреляции для нелинейных форм вычисляется с помощью теоремы о разложении дисперсий по формуле:
где G 2 (y) – это общая дисперсия зависимой переменной;
σ 2 (y) – это объяснённая с помощью построенной модели регрессии дисперсия переменной у, которая рассчитывается по формуле:
δ 2 (y) – необъяснённая или остаточная дисперсия переменной у, которая рассчитывается по формуле:
Также индекс корреляции для нелинейных форм можно рассчитать с помощью теоремы о разложении сумм квадратов по формуле:
где RSS (Regression Sum Square) – сумма квадратов объяснённой регрессии:
ESS (Error Sum Square) – сумма квадратов остатков модели множественной регрессии с n независимыми переменными:
TSS (TotalSumSquare) – общая сумма квадратов модели множественной регрессии с n независимыми переменными:
Индекс корреляции для нелинейных форм связи изменяется в пределах от нуля до единицы. С его помощью нельзя охарактеризовать направление связи между результативной и факторными переменными. Чем ближе значение индекса корреляции для нелинейных форм связи к единице, тем сильнее взаимосвязь между результативной и независимыми переменными, и наоборот, чем ближе значение индекса корреляции для нелинейных форм связи к нулю, тем слабее взаимосвязь между результативной и независимыми переменными.
Индексом детерминации называется квадрат индекса корреляции для нелинейных форм связи.
Расчёт индекса детерминации с помощью теоремы о разложении дисперсий:
Расчёт индекса детерминации с помощью теоремы о разложении сумм квадратов:
Индекс детерминации характеризует, на сколько процентов построенная модель регрессии объясняет вариацию значений результативной переменной относительно своего среднего уровня, т. е. показывает долю общей дисперсии результативной переменной, объяснённой вариацией факторных переменных, включённых в модель регрессии.
Коэффициент множественной детерминации также называется количественной характеристикой объяснённой построенной моделью регрессии дисперсии результативной переменной. Чем больше значение коэффициента множественной детерминации, тем лучше построенная модель регрессии характеризует взаимосвязь между переменными.
Коэффициент детерминации: формулы, расчет, интерпретация, примеры
Коэффициент детерминации: формулы, расчет, интерпретация, примеры — Наука
Содержание:
В коэффициент детерминации — число от 0 до 1, которое представляет долю точек (X, Y), которые следуют за линией регрессии соответствия набора данных с двумя переменными.
Он также известен как степень соответствия и обозначается R 2 . Для его вычисления берется частное между дисперсией данных Ŷi, оцененных с помощью регрессионной модели, и дисперсией данных Yi, соответствующих каждому Xi данных.
Если 100% данных находятся на линии функции регрессии, то коэффициент детерминации будет равен 1.
Напротив, если для набора данных и некоторой функции настройки коэффициент R 2 оказывается равным 0,5, то можно сказать, что посадка на 50% удовлетворительна или хороша.
Аналогично, когда регрессионная модель возвращает значения R 2 ниже 0,5, это означает, что выбранная функция настройки не адаптируется удовлетворительно к данным, поэтому необходимо искать другую функцию настройки.
И когда ковариация или коэффициент корреляции стремится к нулю, то переменные X и Y в данных не связаны, и поэтому R 2 он также будет стремиться к нулю.
Как рассчитать коэффициент детерминации?
В предыдущем разделе было сказано, что коэффициент детерминации рассчитывается путем нахождения частного между дисперсиями:
-Оценено функцией регрессии переменной Y
-То переменной Yi, соответствующей каждой переменной Xi из N пар данных.
Математически это выглядит так:
Из этой формулы следует, что R 2 представляет собой долю дисперсии, объясняемую регрессионной моделью. В качестве альтернативы R можно рассчитать 2 используя следующую формулу, полностью эквивалентную предыдущей:
Где Sε представляет собой дисперсию остатков εi = Ŷi — Yi, а Sy представляет собой дисперсию набора значений Yi данных. Для определения Ŷi применяется функция регрессии, что означает утверждение, что Ŷi = f (Xi).
Дисперсия набора данных Yi, где i от 1 до N, рассчитывается следующим образом:
Sy = [Σ (Yi — ) 2 ) / (N-1)]
А затем поступаем аналогичным образом для Sŷ или для Sε.
Иллюстративный случай
Чтобы показать детали того, как расчет коэффициент детерминации Мы возьмем следующий набор из четырех пар данных:
Для этого набора данных предлагается линейная регрессия, полученная с помощью метода наименьших квадратов:
Применяя эту функцию регулировки, крутящие моменты получаются:
Затем мы вычисляем среднее арифметическое для X и Y:
= (1 + 2 + 3 + 4) / 4 = 2.5
= (1 + 3 + 6 + 7) / 4 = 4.25
Дисперсия Sy
Sy = [(1–4,25) 2 + (3 – 4.25) 2 + (6 – 4.25) 2 +…. ….(7 – 4.25) 2 ] / (4-1)=
= [(-3.25) 2 + (-1.25) 2 + (1.75) 2 + (2.75) 2 ) / (3)] = 7.583
Дисперсия Sŷ
Sŷ = [(1,1 — 4,25) 2 + (3.2 – 4.25) 2 + (5.3 – 4.25) 2 +…. ….(7.4 – 4.25) 2 ] / (4-1)=
= [(-3.25) 2 + (-1.25) 2 + (1.75) 2 + (2.75) 2 ) / (3)] = 7.35
Коэффициент детерминации R 2
р 2 = Sŷ / Sy = 7,35 / 7,58 = 0,97
Интерпретация
Коэффициент детерминации для иллюстративного случая, рассмотренного в предыдущем сегменте, оказался равным 0,98. Другими словами, линейная регулировка через функцию:
Он на 98% надежен в объяснении данных, с которыми он был получен с использованием метода наименьших квадратов.
Помимо коэффициента детерминации, есть коэффициент линейной корреляции или также известный как коэффициент Пирсона. Этот коэффициент, обозначаемый какр, рассчитывается по следующей зависимости:
Здесь числитель представляет собой ковариацию между переменными X и Y, а знаменатель — это произведение стандартного отклонения для переменной X и стандартного отклонения для переменной Y.
Коэффициент Пирсона может принимать значения от -1 до +1. Когда этот коэффициент стремится к +1, существует прямая линейная корреляция между X и Y. Если вместо этого он стремится к -1, существует линейная корреляция, но когда X увеличивается, Y уменьшается. Наконец, он близок к нулю, между двумя переменными нет корреляции.
Следует отметить, что коэффициент детерминации совпадает с квадратом коэффициента Пирсона, только если первый был рассчитан на основе линейной аппроксимации, но это равенство не действует для других нелинейных аппроксимаций.
Примеры
— Пример 1
Группа старшеклассников решила определить эмпирический закон для периода маятника в зависимости от его длины. Для достижения этой цели они проводят серию измерений, в которых измеряют время колебания маятника на разной длине, получая следующие значения:
| Длина (м) | Период (ы) |
|---|---|
| 0,1 | 0,6 |
| 0,4 | 1,31 |
| 0,7 | 1,78 |
| 1 | 1,93 |
| 1,3 | 2,19 |
| 1,6 | 2,66 |
| 1,9 | 2,77 |
| 3 | 3,62 |
Требуется построить диаграмму рассеяния данных и выполнить линейную аппроксимацию через регрессию. Также покажите уравнение регрессии и его коэффициент детерминации.
Решение
Наблюдается довольно высокий коэффициент детерминации (95%), поэтому можно подумать, что линейная аппроксимация является оптимальной. Однако, если рассматривать точки вместе, оказывается, что они имеют тенденцию изгибаться вниз. Эта деталь не рассматривается в линейной модели.
— Пример 2
Для тех же данных в Примере 1 сделайте диаграмму рассеяния данных.В этом случае, в отличие от примера 1, требуется корректировка регрессии с использованием потенциальной функции.
Также покажите функцию подгонки и ее коэффициент детерминации R 2 .
Решение
Потенциальная функция имеет вид f (x) = Ax B , где A и B — константы, определяемые методом наименьших квадратов.
На предыдущем рисунке показана потенциальная функция и ее параметры, а также коэффициент детерминации с очень высоким значением 99%. Обратите внимание на то, что данные соответствуют кривизне линии тренда.
— Пример 3
Используя те же данные из примера 1 и примера 2, выполните полиномиальную аппроксимацию второй степени. Показать график, подобрать полином и коэффициент детерминации R 2 корреспондент.
Решение
При подборе полинома второй степени вы можете увидеть линию тренда, которая хорошо соответствует кривизне данных. Кроме того, коэффициент детерминации выше линейного соответствия и ниже потенциального соответствия.
Сравнение пригодности
Из трех показанных подгонок тот, у которого самый высокий коэффициент детерминации, является потенциальным подгонкой (пример 2).
Подгонка потенциала совпадает с физической теорией маятника, которая, как известно, устанавливает, что период маятника пропорционален квадратному корню из его длины, а коэффициент пропорциональности равен 2π / √g, где g — ускорение свободного падения.
Этот тип потенциального соответствия не только имеет самый высокий коэффициент детерминации, но и показатель степени и константа пропорциональности соответствуют физической модели.
Выводы
— Регулировка регрессии определяет параметры функции, которая направлена на объяснение данных с использованием метода наименьших квадратов. Этот метод состоит в минимизации суммы квадратов разницы между значением Y настройки и значением Yi данных для значений Xi данных. Это определяет параметры функции настройки.
-Как мы видели, наиболее распространенной функцией настройки является линия, но она не единственная, поскольку настройки также могут быть полиномиальными, потенциальными, экспоненциальными, логарифмическими и другими.
-В любом случае коэффициент детерминации зависит от данных и типа корректировки и является показателем качества примененной корректировки.
-Наконец, коэффициент детерминации указывает процент общей изменчивости между значением Y данных по отношению к значению соответствия для данного X.
http://be5.biz/ekonomika/e008/45.html
http://ru1.warbletoncouncil.org/coeficiente-de-determinacion-11466