Значение коэффициента детерминации линейное уравнение регрессии

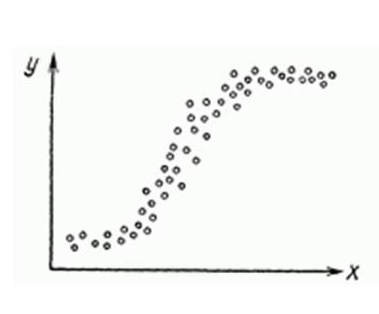
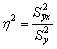Пример нахождения коэффициента детерминации

Коэффициент детерминации рассчитывается для оценки качества подбора уравнения регрессии. Для приемлемых моделей предполагается, что коэффициент детерминации должен быть хотя бы не меньше 50%. Модели с коэффициентом детерминации выше 80% можно признать достаточно хорошими. Значение коэффициента детерминации R 2 = 1 означает функциональную зависимость между переменными.

Для линейной зависимости коэффициент детерминации равен квадрату коэффициента корреляции r_xy: R 2 = r_xy 2 .
2 «>Рассчитать свое значение
Например, значение R 2 = 0.83, означает, что в 83% случаев изменения х приводят к изменению y . Другими словами, точность подбора уравнения регрессии — высокая.

В общем случае, коэффициент детерминации находится по формуле: 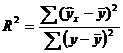или
В этой формуле указаны дисперсии: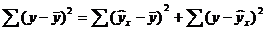
,
где ∑(y- y ) 2 — общая сумма квадратов отклонений;
— сумма квадратов отклонений, обусловленная регрессией («объясненная» или «факторная»);
— остаточная сумма квадратов отклонений.

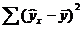
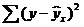
В случае нелинейной регрессии коэффициент детерминации рассчитывается через этот калькулятор. При множественной регрессии, коэффициент детемрминации можно найти через сервис Множественная регрессия

Пример . Дано:

• доля денежных доходов, направленных на прирост сбережений во вкладах, займах, сертификатах и в покупку валюты, в общей сумме среднедушевого денежного дохода, % (Y)
• среднемесячная начисленная заработная плата, тыс. руб. (X)

Следует выполнить: 1. построить поле корреляции и сформировать гипотезу о возможной форме и направлении связи; 2. рассчитать параметры уравнений линейной и A1; 3. выполнить расчет прогнозного значения результата, предполагая, что прогнозные значения факторов составят B2 % от их среднего уровня; 4. оценить тесноту связи с помощью показателей корреляции и детерминации, проанализировать их значения; 5. Дать с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом; 6. Оценить с помощью средней ошибки аппроксимации качество уравнений; 7. Оценить надежность уравнений в целом через F-критерий Фишера для уровня значимости а = 0,05. По значениям характеристик, рассчитанных в пп. 5,6 и данном пункте, выберете лучшее уравнение регрессии и дайте его обоснование.

• Решение онлайн
• Видео решение

Уравнение имеет вид y = ax + b
1. Параметры уравнения регрессии.
Средние значения

Связь между признаком Y фактором X сильная и прямая.
Уравнение регрессии

Коэффициент детерминации для линейной регрессии равен квадрату коэффициента корреляции.
R 2 = 0.91 2 = 0.83, т.е. в 83% случаев изменения х приводят к изменению y. Другими словами — точность подбора уравнения регрессии — высокая

x	y	x 2	y 2	x ∙ y	y(x)	(y-y cp ) 2	(y-y(x)) 2	(x-x p ) 2
15.1	255	228.01	65025	3850.5	505.26	527451.17	62630.22	420.25
17	261	289	68121	4437	549.38	518772.07	83161.41	345.96
12	293	144	85849	3516	433.28	473699.53	19678.51	556.96
10	310	100	96100	3100	386.84	450587.75	5904.58	655.36
74	1425	5476	2030625	105450	1872.88	196906.67	200600	1474.56
83	1985	6889	3940225	164755	2081.86	1007497.33	9381.6	2246.76
85	2549	7225	6497401	216665	2128.3	2457813.93	176990.6	2440.36
81	2012	6561	4048144	162972	2035.42	1062428.38	548.49	2061.16
22	1562	484	2439844	34364	665.47	337260.88	803758.38	184.96
10	386	100	148996	3860	386.84	354332.48	0.71	655.36
4	383	16	146689	1532	247.52	357913.03	18353.53	998.56
14.1	354.1	198.81	125386.81	4992.81	482.04	393327.58	16368.87	462.25
427.2	11775.1	27710.82	19692405.81	709494.31	11775.1	8137990.81	1397376.9	12502.5

2. Оценка параметров уравнения регрессии
Значимость коэффициента корреляции

По таблице Стьюдента находим Tтабл
T_табл (n-m-1;a) = (10;0.05) = 1.812
Поскольку Tнабл > Tтабл , то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициента корреляции статистически — значим

Анализ точности определения оценок коэффициентов регрессии

S _a = 3.3432
Доверительные интервалы для зависимой переменной

Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X = 1
(-557.64;913.38)
Проверка гипотез относительно коэффициентов линейного уравнения регрессии
1) t-статистика

Статистическая значимость коэффициента регрессии a подтверждается (6.95>1.812).

Статистическая значимость коэффициента регрессии b не подтверждается (0.96 Fkp, то коэффициент детерминации статистически значим

R — значит регрессия

Статистика в последнее время получила мощную PR поддержку со стороны более новых и шумных дисциплин — Машинного Обучения и Больших Данных. Тем, кто стремится оседлать эту волну необходимо подружится с уравнениями регрессии. Желательно при этом не только усвоить 2-3 приемчика и сдать экзамен, а уметь решать проблемы из повседневной жизни: найти зависимость между переменными, а в идеале — уметь отличить сигнал от шума.

Для этой цели мы будем использовать язык программирования и среду разработки R, который как нельзя лучше приспособлен к таким задачам. Заодно, проверим от чего зависят рейтинг Хабрапоста на статистике собственных статей.

Введение в регрессионный анализ

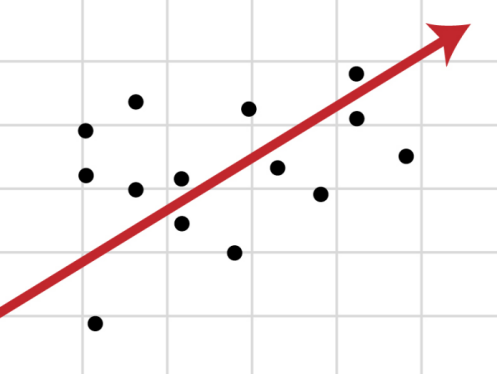
Если имеется корреляционная зависимость между переменными y и x , возникает необходимость определить функциональную связь между двумя величинами. Зависимость среднего значения называется регрессией y по x .

Основу регрессионного анализа составляет метод наименьших квадратов (МНК), в соответствии с которым в качестве уравнения регресии берется функция такая, что сумма квадратов разностей минимальна.

Карл Гаусс открыл, или точнее воссоздал, МНК в возрасте 18 лет, однако впервые результаты были опубликованы Лежандром в 1805 г. По непроверенным данным метод был известен еще в древнем Китае, откуда он перекочевал в Японию и только затем попал в Европу. Европейцы не стали делать из этого секрета и успешно запустили в производство, обнаружив с его помощью траекторию карликовой планеты Церес в 1801 г.

Вид функции , как правило, определен заранее, а с помощью МНК подбираются оптимальные значения неизвестных параметров. Метрикой рассеяния значений вокруг регрессии является дисперсия.

• k — число коэффициентов в системе уравнений регрессии.

Чаще всего используется модель линейной регрессии, а все нелинейные зависимости приводят к линейному виду с помощью алгебраических ухищрений, различных преобразования переменных y и x .

Линейная регрессия

Уравнения линейной регрессии можно записать в виде

В матричном виде это выгладит

• y — зависимая переменная;
• x — независимая переменная;
• β — коэффициенты, которые необходимо найти с помощью МНК;
• ε — погрешность, необъяснимая ошибка и отклонение от линейной зависимости;

Случайная величина может быть интерпретирована как сумма из двух слагаемых:

• — полная дисперсия (TSS).
• — объясненная часть дисперсии (ESS).
• — остаточная часть дисперсии (RSS).

Еще одно ключевое понятие — коэффициент корреляции R 2 .

Ограничения линейной регрессии

Для того, чтобы использовать модель линейной регрессии необходимы некоторые допущения относительно распределения и свойств переменных.

1. Линейность, собственно. Увеличение, или уменьшение вектора независимых переменных в k раз, приводит к изменению зависимой переменной также в k раз.
2. Матрица коэффициентов обладает полным рангом, то есть векторы независимых переменных линейно независимы.
3. Экзогенность независимых переменных — . Это требование означает, что математическое ожидание погрешности никоим образом нельзя объяснить с помощью независимых переменных.
4. Однородность дисперсии и отсутствие автокорреляции. Каждая ε_i обладает одинаковой и конечной дисперсией σ 2 и не коррелирует с другой ε_i. Это ощутимо ограничивает применимость модели линейной регрессии, необходимо удостовериться в том, что условия соблюдены, иначе обнаруженная взаимосвязь переменных будет неверно интерпретирована.

Как обнаружить, что перечисленные выше условия не соблюдены? Ну, во первых довольно часто это видно невооруженным глазом на графике.

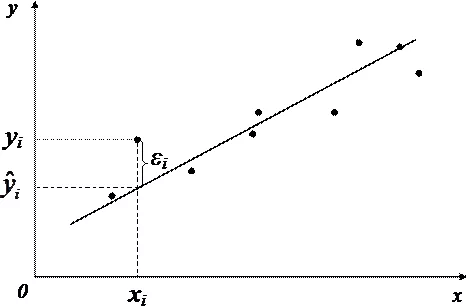
Неоднородность дисперсии

При возрастании дисперсии с ростом независимой переменной имеем график в форме воронки.

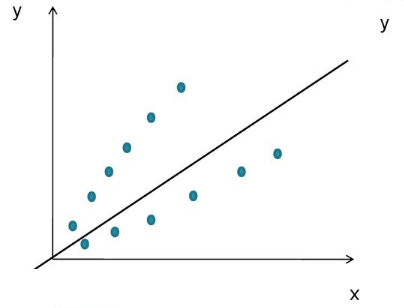
Нелинейную регрессии в некоторых случая также модно увидеть на графике довольно наглядно.

Тем не менее есть и вполне строгие формальные способы определить соблюдены ли условия линейной регрессии, или нарушены.

• Автокорреляция проверяется статистикой Дарбина-Уотсона (0 ≤ d ≤ 4). Если автокорреляции нет, то значения критерия d≈2, при позитивной автокорреляции d≈0, при отрицательной — d≈4.
• Неоднородность дисперсии — Тест Уайта, , при \chi<^2>_<\alpha;m-1>$» data-tex=»inline»/> нулевая гипотеза отвергается и констатируется наличие неоднородной дисперсии. Используя ту же можно еще применить тест Бройша-Пагана.
• Мультиколлинеарность — нарушения условия об отсутствии взаимной линейной зависимости между независимыми переменными. Для проверки часто используют VIF-ы (Variance Inflation Factor).

В этой формуле — коэффициент взаимной детерминации между и остальными факторами. Если хотя бы один из VIF-ов > 10, вполне резонно предположить наличие мультиколлинеарности.

Почему нам так важно соблюдение всех выше перечисленных условий? Все дело в Теореме Гаусса-Маркова, согласно которой оценка МНК является точной и эффективной лишь при соблюдении этих ограничений.

Как преодолеть эти ограничения

Нарушения одной или нескольких ограничений еще не приговор.

1. Нелинейность регрессии может быть преодолена преобразованием переменных, например через функцию натурального логарифма ln .
2. Таким же способом возможно решить проблему неоднородной дисперсии, с помощью ln , или sqrt преобразований зависимой переменной, либо же используя взвешенный МНК.
3. Для устранения проблемы мультиколлинеарности применяется метод исключения переменных. Суть его в том, что высоко коррелированные объясняющие переменные устраняются из регрессии, и она заново оценивается. Критерием отбора переменных, подлежащих исключению, является коэффициент корреляции. Есть еще один способ решения данной проблемы, который заключается в замене переменных, которым присуща мультиколлинеарность, их линейной комбинацией. Этим весь список не исчерпывается, есть еще пошаговая регрессия и другие методы.

К сожалению, не все нарушения условий и дефекты линейной регрессии можно устранить с помощью натурального логарифма. Если имеет место автокорреляция возмущений к примеру, то лучше отступить на шаг назад и построить новую и лучшую модель.

Линейная регрессия плюсов на Хабре

Итак, довольно теоретического багажа и можно строить саму модель.
Мне давно было любопытно от чего зависит та самая зелененькая цифра, что указывает на рейтинг поста на Хабре. Собрав всю доступную статистику собственных постов, я решил прогнать ее через модель линейно регрессии.

Загружает данные из tsv файла.

• points — Рейтинг статьи
• reads — Число просмотров.
• comm — Число комментариев.
• faves — Добавлено в закладки.
• fb — Поделились в социальных сетях (fb + vk).
• bytes — Длина в байтах.

Вопреки моим ожиданиям наибольшая отдача не от количества просмотров статьи, а от комментариев и публикаций в социальных сетях. Я также полагал, что число просмотров и комментариев будет иметь более сильную корреляцию, однако зависимость вполне умеренная — нет надобности исключать ни одну из независимых переменных.

Теперь собственно сама модель, используем функцию lm .

В первой строке мы задаем параметры линейной регрессии. Строка points

. определяет зависимую переменную points и все остальные переменные в качестве регрессоров. Можно определить одну единственную независимую переменную через points

reads , набор переменных — points

Перейдем теперь к расшифровке полученных результатов.

• Intercept — Если у нас модель представлена в виде , то тогда — точка пересечения прямой с осью координат, или intercept .
• R-squared — Коэффициент детерминации указывает насколько тесной является связь между факторами регрессии и зависимой переменной, это соотношение объясненных сумм квадратов возмущений, к необъясненным. Чем ближе к 1, тем ярче выражена зависимость.
• Adjusted R-squared — Проблема с в том, что он по любому растет с числом факторов, поэтому высокое значение данного коэффициента может быть обманчивым, когда в модели присутствует множество факторов. Для того, чтобы изъять из коэффициента корреляции данное свойство был придуман скорректированный коэффициент детерминации .
• F-statistic — Используется для оценки значимости модели регрессии в целом, является соотношением объяснимой дисперсии, к необъяснимой. Если модель линейной регрессии построена удачно, то она объясняет значительную часть дисперсии, оставляя в знаменателе малую часть. Чем больше значение параметра — тем лучше.
• t value — Критерий, основанный на t распределении Стьюдента . Значение параметра в линейной регрессии указывает на значимость фактора, принято считать, что при t > 2 фактор является значимым для модели.
• p value — Это вероятность истинности нуль гипотезы, которая гласит, что независимые переменные не объясняют динамику зависимой переменной. Если значение p value ниже порогового уровня (.05 или .01 для самых взыскательных), то нуль гипотеза ложная. Чем ниже — тем лучше.

Можно попытаться несколько улучшить модель, сглаживая нелинейные факторы: комментарии и посты в социальных сетях. Заменим значения переменных fb и comm их степенями.

Проверим значения параметров линейной регрессии.

Как видим в целом отзывчивость модели возросла, параметры подтянулись и стали более шелковистыми , F-статистика выросла, так же как и скорректированный коэффициент детерминации .

Проверим, соблюдены ли условия применимости модели линейной регрессии? Тест Дарбина-Уотсона проверяет наличие автокорреляции возмущений.

И напоследок проверка неоднородности дисперсии с помощью теста Бройша-Пагана.

В заключение

Конечно наша модель линейной регрессии рейтинга Хабра-топиков получилось не самой удачной. Нам удалось объяснить не более, чем половину вариативности данных. Факторы надо чинить, чтобы избавляться от неоднородной дисперсии, с автокорреляцией тоже непонятно. Вообще данных маловато для сколь-нибудь серьезной оценки.

Но с другой стороны, это и хорошо. Иначе любой наспех написанный тролль-пост на Хабре автоматически набирал бы высокий рейтинг, а это к счастью не так.

Коэффициент детерминации

Коэффициент детерминации (R2)— это доля объяснённой дисперсии отклонений зависимой переменной от её среднего значения. Зависимая переменная объясняется (прогнозируется) с помощью функции от объясняющих переменных, в частном случае является квадратом коэффициента корреляции между зависимой переменной и её прогнозными значениями с помощью объясняющих переменных. Тогда можно сказать, что R2 показывает, какая доля дисперсии результативного признака объясняется влиянием объясняющих переменных.

Формула для вычисления коэффициента детерминации:

где yi — наблюдаемое значение зависимой переменной, а fi — значение зависимой переменной предсказанное по уравнению регрессии -среднее арифметическое зависимой переменной.

Содержание

· 1 Проблемы и общие свойства R2

o 1.1 Интерпретация

o 1.2 Общие свойства для МНК регрессии

o 1.3 Общие свойства для МНК регрессии со свободным членом (единичным фактором)

o 1.4 Мнимая регрессия

· 2 Решение проблем или модификации R2

o 2.1 R2-скорректированный (adjusted)

o 2.2 R2-распространённый (extended)

o 2.3 R2-истинный (несмещённый)

· 3 Прочие используемые критерии

[править]Проблемы и общие свойства R2

[править]Интерпретация

Иногда показателям тесноты связи можно дать качественную оценку (шкала Чеддока):

Количественная мера тесноты связи

Качественная характеристика силы связи

Функциональная связь возникает при значении равном 1, а отсутствие связи — 0. При значениях показателей тесноты связи меньше 0,7 величина коэффициента детерминации всегда будет ниже 50 %. Это означает, что на долю вариации факторных признаков приходится меньшая часть по сравнению с остальными неучтенными в модели факторами, влияющими на изменение результативного показателя. Построенные при таких условиях регрессионные модели имеют низкое практическое значение.

[править]Общие свойства для МНК регрессии

Линейная множественная регрессия методом наименьших квадратов (МНК) — наиболее распространённый случай использования коэффициента детерминации R2.

Линейная множественная МНК регрессия имеет следующие общие свойства [1]:

1. Чем ближе значение к 1 тем ближе модель к эмпирическим наблюдениям.

2. С увеличением количества объясняющих переменных увеличивается R2.

[править]Общие свойства для МНК регрессии со свободным членом (единичным фактором)

Для случая наличия в такой регрессии свободного члена коэффициент детерминации обладает следующими свойствами: [2]

1. принимает значения из интервала (отрезка) [0;1].

2. в случае парной линейной регрессионной МНК модели коэффициент детерминации равен квадрату коэффициента корреляции, то есть R2 = r2. А в случае множественной МНК регрессии R2 = r(y;f)2. Также это квадрат корреляции Пирсона между двумя переменными. Он выражает количество дисперсии, общей между двумя переменными.[3]

3. R2 можно разложить по вкладу каждого фактора в значение R2, причём вклад каждого такого фактора будет положительным. Используется разложение: , где r0j — выборочный коэффициент корреляции зависимой и соответствующей второму индексу объясняющей переменной.

4. R2 связан с проверкой гипотезы о том, что истинные значения коэффициентов при объясняющих переменных равны нулю, в сравнении с альтернативной гипотезой, что не все истинные значения коэффициентов равны нулю. Тогда случайная величина имеет F-распределение с (k-1) и (n-k) степенями свободы.

[править]Мнимая регрессия

Значения R2, , также могут быть манипулированы, с помощью включения фиктивных факторов. Например, если два показателя имеют возрастающую динамику, то их коэффициент корреляции (который входит в факторное разложение) будет достаточно высок. Поэтому логическая и смысловая адекватность модели имеют первостепенную важность. Только качество модели может быль проверено или сопоставлено с использованием R2 и его модификаций.

[править]Решение проблем или модификации R2

[править]R2-скорректированный (adjusted)

Для того, чтобы исследователи не увеличивали R2 с помощью добавления посторонних факторов, R2 заменяется на скорректированный , который даёт штраф за дополнительно включённые факторы, где n — количество наблюдений, а k — количество объясняющих переменных, включая свободный член.>

[править]R2-распространённый (extended)

В случае отсутствия в линейной множественной МНК регрессии свободного члена все четыре вышеперечисленных свойства могут нарушаться для конкретной реализации. Поэтому регрессию со свободным членом и без него нельзя сравнивать по критерию R2. Эта проблема решается с помощью построения распространённого коэффициента детерминации , который будет совпадать с исходным для случая МНК регрессии со свободным членом, и для которого будут продолжать выполняться четыре свойства перечисленые выше. Суть этого метода заключается рассмотрении проекции единичного вектора на плоскость объясняющих переменных [2].
Для случая регрессии без свободного члена:
,
где X — матрица nxk значений факторов, P(X) = X * (X‘ * X) − 1 * X‘ — проектор на плоскость X, , где in — единичный вектор nx1.

с условием небольшой модификации, также подходит для сравнения между собой регрессий построенных с помощью: МНК, обобщённого метода наименьших квадратов (ОМНК), условного метода наименьших квадратов (УМНК), обобщённо-условного метода наименьших квадратов (ОУМНК).

[править]R2-истинный (несмещённый)

[править]Прочие используемые критерии

AIC — информационный критерий Акаике — применяется исключительно для сравнения между моделями. Чем меньше значение тем лучше. Часто используется в виде сравнения моделей временных рядов с разным количеством лагов.
. Даёт меньший штраф за включение лишних лагов в модель, чем BIC.
BIC — информационный критерий Шварца — используется и интерпретируется аналогично AIC.
. Даёт больший штраф за включение лишних лагов в модель, чем BIC (см. формулу). [1]

[править]См. также

§ Дисперсия случайной величины

§ Метод группового учета аргументов

[править]Примечания

1. ↑ 1 2 , , Эконометрика. Начальный курс.. — 6,7,8-е изд., доп. и перераб.. — Москва: Дело, 2004. — Т. «». — 576 с. — ISBN -X

2. ↑ 1 2 Распространение коэффициента детерминации на общий случай линейной регрессии, оцениваемой с помощью различных версий метода наименьших квадратов (рус., англ.) //ЦЕМИ РАН Экономика и математические методы. — Москва: ЦЕМИ РАН, 2002. — В. 3. — Т. 38. — С. 107-120.

3. ↑ , Прикладная статистика. Основы эконометрики (в 2-х т.). — . — Москва: Юнити-Дана (проект TASIS), 2001. — Т. «1,2». — 1088 с. — ISBN -8

4. ↑ Выбор регрессии максимизирующий несмещённую оценку коэффициента детерминации (рус., англ.) // Прикладная эконометрика. — Москва: Маркет ДС, 2008. — В. 4. — Т. 12. — С. 71-83.