Значение параметра b в уравнение

Уравнения с параметром

Разделы: Математика

Справочный материал

Уравнение вида f(x; a) = 0 называется уравнением с переменной х и параметром а.

Решить уравнение с параметром а – это значит, для каждого значения а найти значения х, удовлетворяющие этому уравнению.

Если 1 – а = 0, т.е. а = 1, то х0 = -2 корней нет

Если 1 – а 0, т.е. а 1, то х =

Пример 4.

Если а = 1, то 0х = 0
х – любое действительное число

Если а = -1, то 0х = -2
Корней нет

Если а 1, а -1, то х = (единственное решение).

Это значит, что каждому допустимому значению а соответствует единственное значение х.

если а = 5, то х = = ;

Дидактический материал

3. а = +

4. + 3(х+1)

5. = –

6. =

Ответы:

1. При а1 х =;

1. При а3 х = ;

1. При а1, а-1, а0 х = ;

при а = 1 х – любое действительное число, кроме х = 1

1. При а2, а0 х = ;

1. При а-3, а-2, а0, 5 х =

1. При а + с0, с0 х = ;

Квадратные уравнения с параметром

Пример 1. Решить уравнение

х = –

В случае а 1 выделим те значения параметра, при которых Д обращается в нуль.

Д = (2(2а + 1)) 2 – 4(а – 1)(4а + 30 = 16а 2 + 16а + 4 – 4(4а 2 + 3а – 4а – 3) = 16а 2 + 16а + 4 – 16а 2 + 4а + 12 = 20а + 16

a =

a =

Если а -4/5 и а 1, то Д > 0,

х =

х = – = –

Пример 2. При каких значениях параметра а уравнение

х 2 + 2(а + 1)х + 9а – 5 = 0 имеет 2 различных отрицательных корня?

В итоге

4(а – 1)(а – 6) > 0 — 2(а + 1) 0

а 6 а > — 1 а > 5/9

6

Пример 3. Найдите значения а, при которых данное уравнение имеет решение.

Д = 4(а – 1) 2 – 4(2а + 10 = 4а 2 – 8а + 4 – 8а – 4 = 4а 2 – 16а

4а 2 – 16 0

4а(а – 4) 0

а(а – 4)) 0

Ответ: а 0 и а 4

Дидактический материал

1. При каком значении а уравнение ах 2 – (а + 1) х + 2а – 1 = 0 имеет один корень?

2. При каком значении а уравнение (а + 2) х 2 + 2(а + 2)х + 2 = 0 имеет один корень?

3. При каких значениях а уравнение (а 2 – 6а + 8) х 2 + (а 2 – 4) х + (10 – 3а – а 2 ) = 0 имеет более двух корней?

4. При каких значениях а уравнение 2х 2 + х – а = 0 имеет хотя бы один общий корень с уравнением 2х 2 – 7х + 6 = 0?

5. При каких значениях а уравнения х 2 +ах + 1 = 0 и х 2 + х + а = 0 имеют хотя бы один общий корень?

Показательные уравнения с параметром

Пример 1.Найти все значения а, при которых уравнение

9 х – (а + 2)*3 х-1/х +2а*3 -2/х = 0 (1) имеет ровно два корня.

Решение. Умножив обе части уравнения (1) на 3 2/х , получим равносильное уравнение

3 2(х+1/х) – (а + 2)*3 х+1/х + 2а = 0 (2)

Пусть 3 х+1/х = у, тогда уравнение (2) примет вид у 2 – (а + 2)у + 2а = 0, или

Если у = 2, т.е. 3 х+1/х = 2 то х + 1/х = log₃2 , или х 2 – хlog₃2 + 1 = 0.

Это уравнение не имеет действительных корней, так как его Д = log 2 ₃2 – 4 х+1/х = а то х + 1/х = log₃а, или х 2 – хlog₃а + 1 = 0. (3)

Уравнение (3) имеет ровно два корня тогда и только тогда, когда

Д = log 2 ₃2 – 4 > 0, или |log₃а| > 2.

Если log₃а > 2, то а > 9, а если log₃а 9.

Пример 2. При каких значениях а уравнение 2 2х – (а – 3) 2 х – 3а = 0 имеет решения?

Для того чтобы заданное уравнение имело решения, необходимо и достаточно, чтобы уравнение t 2 – (a – 3) t – 3a = 0 имело хотя бы один положительный корень. Найдем корни по теореме Виета: х₁ = -3, х₂ = а = >

а – положительное число.

Дидактический материал

1. Найти все значения а, при которых уравнение

25 х – (2а + 5)*5 х-1/х + 10а * 5 -2/х = 0 имеет ровно 2 решения.

2. При каких значениях а уравнение

2 (а-1)х?+2(а+3)х+а = 1/4 имеет единственный корень?

3. При каких значениях параметра а уравнение

4 х — (5а-3)2 х +4а 2 – 3а = 0 имеет единственное решение?

Ответ:

1. 0 25/2
2. при а = 1, а = -2,2
3. 0 0, х1/4 (3)

х = у

Если а = 0, то –

2у + 1 = 0 2у = 1 у = 1/2 х = 1/2 х = 1/4

Не выполняется (2) условие из (3).

Пусть а 0, то ау 2 – 2у + 1 = 0 имеет действительные корни тогда и только тогда, когда Д = 4 – 4а 0, т.е. при а 1.

Если Д = 0 (а = 1), то (4) имеет единственный положительный корень х = 1, удовлетворяющий условиям (3).

Пусть Д > 0 (а 0 уравнение (4) имеет действительные корни разных знаков. Это условие выполняется тогда и только тогда, когда Д > 0 и 1/а х

Выражая х из (1) и подставляя в (2), получаем неравенство

2 – а > 1 – а (3)

Чтобы решить неравенство (3), построим графики функций у = 2 – а и у = 1 – а.

Решения неравенства (3) образуют промежуток (а₀; 2), где а₀ 2

а₀ =

Ответ: x + 9a 3 ) = x имеет ровно два корня.

Ответы:

при а 16.06.2009

Уравнения с параметрами.

Исследование и решение уравнений с параметрами считается не самым простым разделом школьной математики. Однако, параметр, как понятие, часто воспринимается школьниками гораздо более сложным, чем есть в действительности. Здесь в первом пункте представлены очень простые вводные примеры использования параметров в уравнениях. Те, для кого это понятие не составляет большой трудности, могут сразу перейти к решению задач, которые представлены ниже.

Что такое уравнение с параметром?

Допустим нам нужно решить уравнение 2х + 5 = 2 − x.
Решение: 2x + x = 2 − 5; 3x = −3; x = −3/3 = −1.

Теперь нужно решить уравнение 2x + 5 = 3 − x.
Решение: 2x + x = 3 − 5; 3x = −2; x = −2/3

Затем нужно решить уравнение 2x + 5 = 0,5 − x.
Решение: 2x + x = 0,5 − 5; 3x = −4,5; x = −4,5/3 = −1,5.

А потом может потребоваться решить уравнение 2x + 5 = 10,7 − x или уравнение 2x + 5 = −0,19 − x.
Понятно, что уравнения похожи, а потому их решение будет сопровождаться теми же действиями, что выше. Возникает естественный вопрос — сколько можно делать одно и то же?

Уменьшим себе трудозатраты. Заметим, что все эти уравнения отличаются только одним числом в правой части. Обозначим это число символом a .
Получим уравнение 2х + 5 = a − х,
где a — переменная величина, вместо которой можно подставить нужное числовое значение и получить нужное уравнение. Эта переменная и называется параметром.

Решим это уравнение так же, как и все предыдущие.
Решение: 2х + 5 = a − x; 2x + x = a − 5; 3x = a − 5; x = (a − 5)/3.

Теперь для того, чтобы найти ответы для двух последних примеров, мы можем не повторять полностью всё решение каждого уравнения, а просто подставить в полученную формулу для х числовое значение параметра а:
x = (10,7 − 5)/3 = 5,7/3 = 1,9;
x = (−0,19 − 5)/3 = −5,19/3 = −1,73.

Таким образом, под термином «уравнение с параметром», фактически, скрывается целое семейство «почти одинаковых уравнений» , которые отличаются друг от друга только одним числом (одним слагаемым или одним коэффициентом) и одинаково решаются. Параметр — это число, которое меняется от уравнения к уравнению.
Полученную формулу для корня уравнения мы можем запрограммировать на компьютере. Достаточно будет только ввести значение параметра a, чтобы получить решение любого такого уравнения.

Рассмотрим еще один пример.

Замечаем, что они похожи друг на друга и отличаются только первым коэффициентом. Обозначим его, например, символом k.
Решим уравнение kх + 5 = 2 − x с параметром k.

С помощью этой формулы вычислим все ответы для приведенных уравнений.
x = −3/(2 + 1) = −1
x = −3/(3 + 1) = −0,75
x = −3/(−4 + 1) = 1
x = −3/(17 + 1) = −1/6

Можем ли мы теперь запрограммировать эту формулу и сказать, что с её помощью можно решить любое аналогичное уравнение?
Запрограммировать можем. Компьютер справится как с очень большими значениями коэффициента, так и с очень маленькими.
Например, если введём k = 945739721, то для уравнения заданного вида будет получен корень примерно равный −0,0000000031721201195353831188, если k = 0,0000004, то получим корень ≈ −2,9999988000004799998080000768.
Но, если мы введем в программу, казалось бы, более простое значение k = −1, то компьютер зависнет.
Почему?

Посмотрим внимательнее на формулу x = −3/(−1 + 1) = −3/0. Деление на ноль.
Посмотрим на соответствующее уравнение −1·х + 5 = 2 − x.
Преобразуем его −х + x = 2 − 5.
Оказывается, оно равносильно уравнению 0 = −3 (. ) и не может иметь корней.
Таким образом, из общего подхода к решению «почти одинаковых уравнений» могут существовать исключения, о которых нужно позаботиться отдельно. Т.е. провести предварительное исследование всего семейства уравнений. Именно этому и учатся на уроках математики с помощью так называемых задач с параметрами.

Графические способы решения уравнений

Сначала вспомним, что представляет собой графический способ решения обычного уравнения (без параметра).
Пусть дано уравнение вида f(x) = g(x) . Построим графики функций y = f(x) и y = g(x) и найдём точки пересечения этих графиков. Абсциссы точек пересечения и есть корни уравнения.

Для быстрого построения эскизов графиков повторите еще раз графики элементарных функций, которые изучаются в школьном курсе математики, и правила преобразования графиков функций.

Рассмотрим примеры.

1. Решить уравнение
2х + 5 = 2 − x

Ответ: x = −1.

2. Решить уравнение
2х 2 + 4х − 1 = 2х + 3

3. Решить уравнение
log₂х = −0,5х + 4

Ответ: x = 2.

Первые два из приведенных уравнений вы можете решить и аналитически, так как это обычные линейное и квадратное уравнения. Второе уравнение содержит функции разных классов — степенную (здесь линейную) и трансцендентную (здесь логарифмическую). Для таких случаев выбор способов решения у школьников очень ограничен. Фактически, единственным доступным способом является именно графическое решение.

Внимание: Для корней, найденных графическим способом, обязательна проверка! Вы уверены, что на третьем рисунке пересечение именно в точке х = 4 , а не в точке 3,9 или 4,1? А если на реальном экзамене у вас нет возможности построить график достаточно точно? На чертеже «от руки» разброс может быть еще больше. Поэтому алгоритм действий должен быть следующим:

1. Предварительный вывод: х ≈ 4.
2. Проверка: log₂4 = −0,5·4 + 4; 2 = −2 + 4; 2 ≡ 2.
3. Окончательный вывод х = 4.

Чтобы графически решать уравнения с параметрами надо строить не отдельные графики, а их семейства.

Решение уравнений с параметрами с помощью графиков.

Задача 1.

Найти все значения параметра q при которых уравнение |x + 1| − |x − 3| − x = q 2 − 8q + 13 имеет ровно 2 корня.

При каждом значении параметра q можно вычислить значение выражения q 2 − 8q + 13 . Результат обозначим переменной а.
Т.е. примем q 2 − 8q + 13 = a и решим уравнение с параметром |x + 1| − |x − 3| − x = a

Строим график функции y = |x + 1| − |x − 3| − x , расположенной в левой части уравнения.
Для этого разобьём числовую ось на отрезки точками, в которых каждый из встречающихся модулей принимает нулевое значение.

Для каждого из этих участков раскроем модули с учётом знаков.
Вспомним: по определению |x| = x, если х ≥ 0, и |x| = −x, если х Чтобы проверить знаки модулей на участке достаточно подставить любое промежуточное значение x из этого отрезка, например, −2, 0 и 4.

Таким образом на участке I, где −∞ имеем −(x + 1) + (x − 3) − x = − x − 4.
Следовательно, должны построить график функции y = − x − 4 .
Это линейная функция. Её график прямая линия, которую можно построить по двум точкам, например, x = 0, y = −4 и у = 0, x = −4. Cтроим всю прямую бледной линией, а затем выделяем часть графика, относящуюся только к рассматриваемому участку.

Аналогично, разбираемся с оставшимися двумя участками.

На участке II, где −1 имеем (x + 1) + (x − 3) − x = x − 2
и должны построить соответствующую часть графика функции y = x − 2 .

На участке III, где 3 , имеем (x + 1) − (x − 3) − x = − x + 4
и должны построить соответствующую часть графика функции y = − x + 4 .

Последовательное построение итогового графика показано ниже. (Чтобы увеличить рисунок, нужно щелкнуть по нему левой кнопкой мыши.)

Замечание: если вы освоили тему Преобразование графиков функций, то с этой частью задачи сможете справиться быстрее, чем показано в примере.

Итак, построение графика функции, расположенной в левой части уравнения, мы завершили. Посмотрим, что находится в правой части.

График функции y = a представляет собой прямую линию, параллельную оси абсцисс (Ox), и пересекающую ось ординат (Oy) в точке а. Так как а — параметр, который может принимать разные значения, то нужно построить целое семейство таких параллельных линий, пересекающих ось ординат на разной высоте. Очевидно, что все графики семейства построить мы не сможем, поскольку их бесконечное множество. Изобразим для примера несколько штук в районе уже построенного графика функции. Ниже прямые семейства y = a показаны красным цветом.

Из рисунка видно, что количество точек пересечения каждой из красных прямых с ранее построенным (зелёным) графиком зависит от высоты, на которой расположена эта прямая, т.е. от параметра а. Прямые, расположенные ниже y = −3 , пересекают график в одной точке, а значит эти уравнения имеют только одно решение. Прямые, проходящие на уровне −3 имеют по три точки пересечения, значит соответствующие уравнения будут иметь по три решения. Прямые, расположенные выше точки y = 1 , снова имеют только по одной точке пересечения.
Ровно две точки пересечения с зелёным графиком будут иметь только прямые y = 1 и y = −3 . Соответствующие уравнения будут иметь ровно два корня, что и требовалось определить в задании.

Однако мы нашли значения введённого нами параметра а, при котором заданное уравнение имеет 2 корня, а вопрос задачи состоял в том, чтобы найти все значения параметра q. Для этого придётся решить следующую совокупность уравнений:

Это обычные квадратные уравнения, которые решаются через дискриминант или по теореме Виета.

Таким образом, окончательный ответ: <2;4;6>.

Задача 2.

Найти все значения параметра a, при которых уравнение (2 − x)x(x − 4) = a имеет ровно 3 корня.

Рассмотрим функцию y = (2 − x)x(x − 4) . Видно, что если раскрыть скобки, то старший член будет −х 3 . Т.е. графиком функции должна быть кубическая парабола, причем на при x, стремящемcя к +∞, y → −∞, а при x, стремящемся к −∞, y → +∞.
Поскольку уравнение (2 − x)x(x − 4) = 0 имеет три корня 2, 0 и 4, то график функции будет пересекать ось абсцисс трижды.
Понятно, что при упомянутых условиях график непрерывной функции должен иметь участок с «волной». Строим от руки эскиз графика.

Правая часть уравнения y = a такая же, как в предыдущей задаче. Поэтому дальнейшие построения не требуют комментариев. Смотрите рисунки. Чтобы увеличить, используйте щелчок мышью.

Из рисунков видно, что прямые, отделяющие линии с тремя точками пересечения от других случаев, проходят через экстремумы кубической функции. Поэтому определяем значения y_max и y_min через производную. (Исследовать функцию полностью не нужно, так как примерное положение точек экстремума мы видим на эскизе графика.) Обратите внимание на то, что при вычислении значений функции используются точные значения x и формулы сокращенного умножения. Приближенные значения в промежуточных вычислениях не используют.

Ответ:

Задача для самостоятельного решения

Задача 3.

При каком наибольшем отрицательном значении параметра а уравнение имеет один корень?

Ответ: -1,625

Задача реального экзамена ЗНО-2013 (http://www.osvita.ua/).

Переход на главную страницу сайта «Математичка».

Есть вопросы? пожелания? замечания?
Обращайтесь — mathematichka@yandex.ru

Внимание, ©mathematichka. Прямое копирование материалов на других сайтах запрещено. Ставьте гиперссылку.

Подбор параметра в EXCEL

history 18 ноября 2012 г.

Группы статей
• Другие Стандартные Средства

Обычно при создании формулы пользователь задает значения параметров и формула (уравнение) возвращает результат. Например, имеется уравнение 2*a+3*b=x, заданы параметры а=1, b=2, требуется найти x (2*1+3*2=8). Инструмент Подбор параметра позволяет решить обратную задачу: подобрать такое значение параметра, при котором уравнение возвращает желаемый целевой результат X. Например, при a=3, требуется найти такое значение параметра b, при котором X равен 21 (ответ b=5). Подбирать параметр вручную — скучное занятие, поэтому в MS EXCEL имеется инструмент Подбор параметра .

В MS EXCEL 2007-2010 Подбор параметра находится на вкладке Данные, группа Работа с данным .

Простейший пример

Найдем значение параметра b в уравнении 2*а+3*b=x , при котором x=21 , параметр а= 3 .

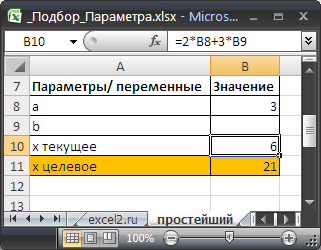
Подготовим исходные данные.

Значения параметров а и b введены в ячейках B8 и B9 . В ячейке B10 введена формула =2*B8+3*B9 (т.е. уравнение 2*а+3*b=x ). Целевое значение x в ячейке B11 введено для информации.

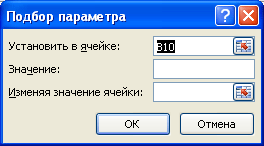
Выделите ячейку с формулой B10 и вызовите Подбор параметра (на вкладке Данные в группе Работа с данными выберите команду Анализ «что-если?» , а затем выберите в списке пункт Подбор параметра …) .

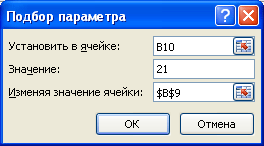
В качестве целевого значения для ячейки B10 укажите 21, изменять будем ячейку B9 (параметр b ).

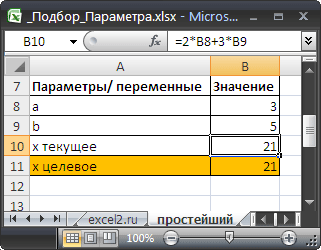
Инструмент Подбор параметра подобрал значение параметра b равное 5.

Конечно, можно подобрать значение вручную. В данном случае необходимо в ячейку B9 последовательно вводить значения и смотреть, чтобы х текущее совпало с Х целевым. Однако, часто зависимости в формулах достаточно сложны и без Подбора параметра параметр будет подобрать сложно .

Примечание : Уравнение 2*а+3*b=x является линейным, т.е. при заданных a и х существует только одно значение b , которое ему удовлетворяет. Поэтому инструмент Подбор параметра работает (именно для решения таких линейных уравнений он и создан). Если пытаться, например, решать с помощью Подбора параметра квадратное уравнение (имеет 2 решения), то инструмент решение найдет, но только одно. Причем, он найдет, то которое ближе к начальному значению (т.е. задавая разные начальные значения, можно найти оба корня уравнения). Решим квадратное уравнение x^2+2*x-3=0 (уравнение имеет 2 решения: x1=1 и x2=-3). Если в изменяемой ячейке введем -5 (начальное значение), то Подбор параметра найдет корень = -3 (т.к. -5 ближе к -3, чем к 1). Если в изменяемой ячейке введем 0 (или оставим ее пустой), то Подбор параметра найдет корень = 1 (т.к. 0 ближе к 1, чем к -3). Подробности в файле примера на листе Простейший .

Еще один путь нахождения неизвестного параметра b в уравнении 2*a+3*b=X — аналитический. Решение b=(X-2*a)/3) очевидно. Понятно, что не всегда удобно искать решение уравнения аналитическим способом, поэтому часто используют метод последовательных итераций, когда неизвестный параметр подбирают, задавая ему конкретные значения так, чтобы полученное значение х стало равно целевому X (или примерно равно с заданной точностью).

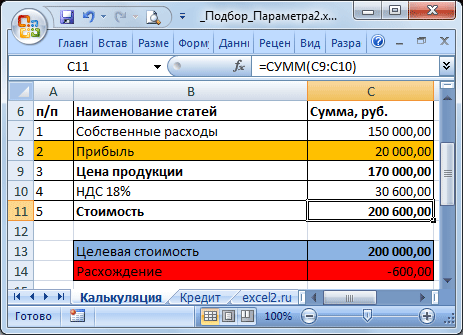
Калькуляция, подбираем значение прибыли

Еще пример. Пусть дана структура цены договора: Собственные расходы, Прибыль, НДС.

Известно, что Собственные расходы составляют 150 000 руб., НДС 18%, а Целевая стоимость договора 200 000 руб. (ячейка С13 ). Единственный параметр, который можно менять, это Прибыль. Подберем такое значение Прибыли ( С8 ), при котором Стоимость договора равна Целевой, т.е. значение ячейки Расхождение ( С14 ) равно 0.

В структуре цены в ячейке С9 (Цена продукции) введена формула Собственные расходы + Прибыль ( =С7+С8 ). Стоимость договора (ячейка С11 ) вычисляется как Цена продукции + НДС (= СУММ(С9:C10) ).

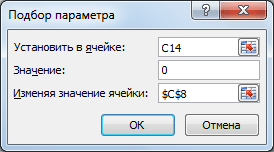
Конечно, можно подобрать значение вручную, для чего необходимо уменьшить значение прибыли на величину расхождения без НДС. Однако, как говорилось ранее, зависимости в формулах могут быть достаточно сложны. В этом случае поможет инструмент Подбор параметра .

Выделите ячейку С14 , вызовите Подбор параметра (на вкладке Данные в группе Работа с данными выберите команду Анализ «что-если?» , а затем выберите в списке пункт Подбор параметра …). В качестве целевого значения для ячейки С14 укажите 0, изменять будем ячейку С8 (Прибыль).

Теперь, о том когда этот инструмент работает. 1. Изменяемая ячейка не должна содержать формулу, только значение.2. Необходимо найти только 1 значение, изменяя 1 ячейку. Если требуется найти 1 конкретное значение (или оптимальное значение), изменяя значения в НЕСКОЛЬКИХ ячейках, то используйте Поиск решения.3. Уравнение должно иметь решение, в нашем случае уравнением является зависимость стоимости от прибыли. Если целевая стоимость была бы равна 1000, то положительной прибыли бы у нас найти не удалось, т.к. расходы больше 150 тыс. Или например, если решать уравнение x2+4=0, то очевидно, что не удастся подобрать такое х, чтобы x2+4=0

Примечание : В файле примера приведен алгоритм решения Квадратного уравнения с использованием Подбора параметра.

Подбор суммы кредита

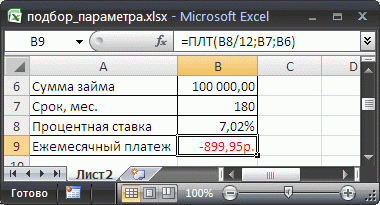
Предположим, что нам необходимо определить максимальную сумму кредита , которую мы можем себе позволить взять в банке. Пусть нам известна сумма ежемесячного платежа в рублях (1800 руб./мес.), а также процентная ставка по кредиту (7,02%) и срок на который мы хотим взять кредит (180 мес).

В EXCEL существует функция ПЛТ() для расчета ежемесячного платежа в зависимости от суммы кредита, срока и процентной ставки (см. статьи про аннуитет ). Но эта функция нам не подходит, т.к. сумму ежемесячного платежа мы итак знаем, а вот сумму кредита (параметр функции ПЛТ() ) мы как раз и хотим найти. Но, тем не менее, мы будем использовать эту функцию для решения нашей задачи. Без применения инструмента Подбор параметра сумму займа пришлось бы подбирать в ручную с помощью функции ПЛТ() или использовать соответствующую формулу.

Введем в ячейку B 6 ориентировочную сумму займа, например 100 000 руб., срок на который мы хотим взять кредит введем в ячейку B 7 , % ставку по кредиту введем в ячейку B8, а формулу =ПЛТ(B8/12;B7;B6) для расчета суммы ежемесячного платежа в ячейку B9 (см. файл примера ).

Чтобы найти сумму займа соответствующую заданным выплатам 1800 руб./мес., делаем следующее:

• на вкладке Данные в группе Работа с данными выберите команду Анализ «что-если?» , а затем выберите в списке пункт Подбор параметра …;
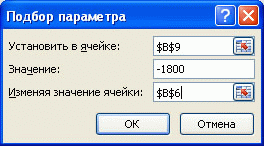
• в поле Установить введите ссылку на ячейку, содержащую формулу. В данном примере — это ячейка B9 ;
• введите искомый результат в поле Значение . В данном примере он равен -1800 ;
• В поле Изменяя значение ячейки введите ссылку на ячейку, значение которой нужно подобрать. В данном примере — это ячейка B6 ;
• Нажмите ОК

Что же сделал Подбор параметра ? Инструмент Подбор параметра изменял по своему внутреннему алгоритму сумму в ячейке B6 до тех пор, пока размер платежа в ячейке B9 не стал равен 1800,00 руб. Был получен результат — 200 011,83 руб. В принципе, этого результата можно было добиться, меняя сумму займа самостоятельно в ручную.

Подбор параметра подбирает значения только для 1 параметра. Если Вам нужно найти решение от нескольких параметров, то используйте инструмент Поиск решения . Точность подбора параметра можно задать через меню Кнопка офис/ Параметры Excel/ Формулы/ Параметры вычислений . Вопросом об единственности найденного решения Подбор параметра не занимается, вероятно выводится первое подходящее решение.

Иными словами, инструмент Подбор параметра позволяет сэкономить несколько минут по сравнению с ручным перебором.