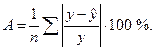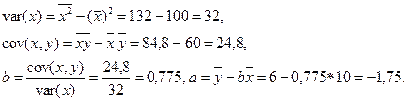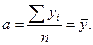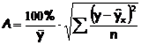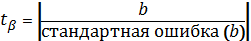Средняя ошибка аппроксимации
По семи территориям Уральского района за 199Х г. известны значения двух признаков.
| Район | Расходы на покупку продовольственных товаров в общих расходах, %, у | Среднедневная заработная плата одного работающего, руб., х |
| Удмуртская респ. | 68,8 | 45,1 |
| Свердловская обл. | 61,2 | 59,0 |
| Башкортостан | 59,9 | 57,2 |
| Челябинская обл. | 56,7 | 61,8 |
| Пермская обл. | 55,0 | 58,8 |
| Курганская обл. | 54,3 | 47,2 |
| Оренбургская обл. | 49,3 | 55,2 |
1. Для характеристики зависимости у от х рассчитать параметры следующих функций:
а) линейной;
б) степенной;
в) показательной;
г) равносторонней гиперболы (так же нужно придумать как предварительно линеаризовать данную модель).
2. Оценить каждую модель через среднюю ошибку аппроксимации Аср и F-критерий Фишера.
Решение проводим при помощь онлайн калькулятора Линейное уравнение регрессии.
а) линейное уравнение регрессии;
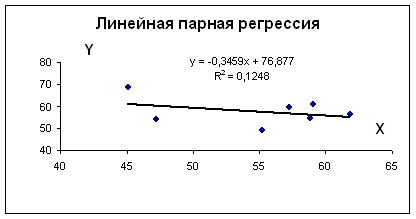
Использование графического метода.
Этот метод применяют для наглядного изображения формы связи между изучаемыми экономическими показателями. Для этого в прямоугольной системе координат строят график, по оси ординат откладывают индивидуальные значения результативного признака Y, а по оси абсцисс — индивидуальные значения факторного признака X.
Совокупность точек результативного и факторного признаков называется полем корреляции.
Для наших данных система уравнений имеет вид
Из первого уравнения выражаем а и подставим во второе уравнение
Получаем b = -0.35, a = 76.88
Уравнение регрессии: y = -0.35 x + 76.88
| x | y | x 2 | y 2 | x • y | y(x) | (y i -y cp ) 2 | (y-y(x)) 2 | |y — y x |:y |
| 45,1 | 68,8 | 2034,01 | 4733,44 | 3102,88 | 61,28 | 119,12 | 56,61 | 0,1094 |
| 59 | 61,2 | 3481 | 3745,44 | 3610,8 | 56,47 | 10,98 | 22,4 | 0,0773 |
| 57,2 | 59,9 | 3271,84 | 3588,01 | 3426,28 | 57,09 | 4,06 | 7,9 | 0,0469 |
| 61,8 | 56,7 | 3819,24 | 3214,89 | 3504,06 | 55,5 | 1,41 | 1,44 | 0,0212 |
| 58,8 | 55 | 3457,44 | 3025 | 3234 | 56,54 | 8,33 | 2,36 | 0,0279 |
| 47,2 | 54,3 | 2227,84 | 2948,49 | 2562,96 | 60,55 | 12,86 | 39,05 | 0,1151 |
| 55,2 | 49,3 | 3047,04 | 2430,49 | 2721,36 | 57,78 | 73,71 | 71,94 | 0,172 |
| 384,3 | 405,2 | 21338,41 | 23685,76 | 22162,34 | 405,2 | 230,47 | 201,71 | 0,5699 |
Примечание: значения y(x) находятся из полученного уравнения регрессии:
y(45.1) = -0.35*45.1 + 76.88 = 61.28
y(59) = -0.35*59 + 76.88 = 56.47
. . .
Ошибка аппроксимации
Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации. Средняя ошибка аппроксимации — среднее отклонение расчетных значений от фактических:
F-статистики. Критерий Фишера.
Проверка значимости модели регрессии проводится с использованием F-критерия Фишера, расчетное значение которого находится как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещенной оценки дисперсии остаточной последовательности для данной модели.
Если расчетное значение с k1=(m) и k2=(n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой.
где m – число факторов в модели.
Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:
1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H0: R 2 =0 на уровне значимости α.
2. Далее определяют фактическое значение F-критерия:
где m=1 для парной регрессии.
3. Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 1 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2.
4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу.
В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом.
Табличное значение критерия со степенями свободы k1=1 и k2=5, Fkp = 6.61
Поскольку фактическое значение F b
в) показательная регрессия;
г) модель равносторонней гиперболы.
Система нормальных уравнений.
Для наших данных система уравнений имеет вид
7a + 0.1291b = 405.2
0.1291a + 0.0024b = 7.51
Из первого уравнения выражаем а и подставим во второе уравнение
Получаем b = 1054.67, a = 38.44
Уравнение регрессии:
y = 1054.67 / x + 38.44
Ошибка аппроксимации.
Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации.
Средняя ошибка аппроксимации
Оценку качества построенной модели дает коэффициент детерминации, а также средняя ошибка аппроксимации.
Средняя ошибка аппроксимации – среднее отклонение расчетных значений зависимой переменной от фактических:
Допустимый предел значений A – не более 8-10 %.
Пример 2.5. Построим регрессионные зависимости: а) расходов на питание (y) и личным доходом (x); б) расходов на питание (y) и временем (t) по следующим данным (усл. ед.):
| Год |
| X |
| Y |
и оценим качество подгонки.
а) Пусть истинная модель описывается выражением y = a + b x + e.
По выборочным наблюдениям определяем оценки (a; b).
Исходные данные и расчетные показатели представим в виде следующей расчетной таблицы:
| Год | X | Y | X 2 | Xy |  |  |  |  |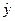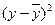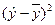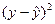
| -0,2 | 38,44 | 1,44 | ||||||
| 2,9 | 9,61 | 0,81 | ||||||
| 9,1 | 9,61 | 3,61 | ||||||
| 12,2 | 38,44 | 0,04 | ||||||
| Итого | 96,1 | 9,9 | ||||||
| Сред. | 84,8 | 21,2 | 19,22 | 1,98 | ||||
 |  |  |  |  |  |  |  |
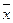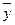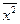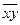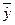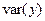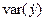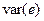Cледовательно,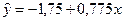 
.
Коэффициент b = 0,775 показывает, что при увеличения дохода на 1 усл. ед расходы на питание увеличиваются в среднем на 0,775 усл. ед.
Замечание.В Excel оценки (a, b) можно также определить с помощью функций:
Условие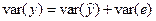 
выполняется.
Качество подгонки оцениваем коэффициентом детерминации:
, т.е. 90,7 % вариации зависимой переменной (расходы на питание) объясняется регрессией.
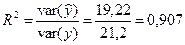
Значимость коэффициента R 2 проверяем по F-тесту
.
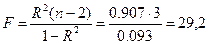
Произведем проверку значимости R 2 двумя способами.
1. При α = 0,05, n1= 1 и n2 = 3 по таблице или с помощью функции FРАСПОБР(α; n1; n2) находим Fкр = 10,13. Поскольку F = 29,2 > Fкр = 10,13, то R 2 = 0,952 значим при 5 % уровне.
2. Наблюдаемому (расчетному) значению критерия F = 29,2 соответствует значимость F =0,0124, которую можно определить в Excel с помощью функции FРАСП(F; n1; n2).
Поскольку значимостьF = 0,0124 2 значим при уровне 5 %.
б) Пусть истинная модель y = a + b t + e, (модель временного ряда). Выборочная регрессия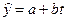 
, где t – время, определяемое как t = 1 для 1990 г., t = 2 для 1991 г. и т.д.
Представим исходные и расчетные показатели в виде расчетной таблицы:
| Год | t | Y | t 2 | ty | |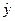
| –0,2 | |||||
| 2,9 | |||||
| 9,1 | |||||
| 12,2 | |||||
| Итого | |||||
| Среднее | 24,2 | ||||
 | |  |  | |
, следовательно, 
.
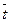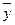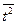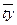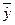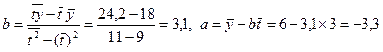
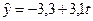
Коэффициент b = 3,1 показывает, что за год расходы на питание в среднем возрастают на 3,1 единиц.
Пример 2.6. Покажем, что в модели регрессии без свободного члена
Y = b X + e оценка МНК дляbесть:
.
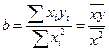
Выборочная регрессия для этой модели есть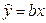 
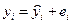
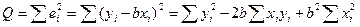
. Наблюдаемые значения зависимой переменной связаны с расчетными уравнением 
. Оценку b найдем из минимизации величины:
.
Запишем необходимые условия экстремума:
, откуда 
.
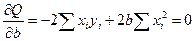
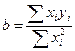
Вычисление R 2 при отсутствии свободного члена некорректно; при этом не выполняется условие .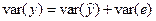
Пример 2.7. Покажем, что в модели регрессии Y = a + e оценка МНК для a есть: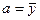 
.
Выборочная регрессия для заданной модели есть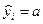 
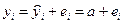
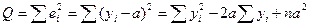
. Наблюдаемые значения зависимой переменной связаны с расчетными значениями уравнением: 
. Оценку a найдем из минимизации величины
.
Запишем необходимые условия экстремума:
откуда 
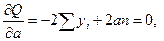
Выборочная регрессия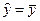 
.
Расчет средней ошибки аппроксимации. Практическое применение
СОА показывает среднее отклонение расчетных данных результативного признака от фактических. Допустимый предел 8-10%.
Величина отклонений фактических и расчетных значений результативного признака 
по каждому наблюдению представляет собой ошибку аппроксимации.
Поскольку 
может быть как величиной положительной, так и отрицательной, то ошибки аппроксимации для каждого наблюдения принято определять в процентах по модулю.
Отклонения можно рассматривать как абсолютную ошибку аппроксимации, а 
— как относительную ошибку аппроксимации
Чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению определяют среднюю ошибку аппроксимации: 
Возможно и иное определение средней ошибки аппроксимации: 
Если А =10-12%, то можно говорить о хорошем качестве модели.
Смысл средней ошибки аппроксимации в том, что это один из многих способов оценить разницу между аппроксимированнм и реальным значениями изучаемой величины. То есть это «квантификатор» потерь (в экономическом смысле) или риска.
27) Эластичность в социально-экономических моделях. Частные коэффициенты эластичности. Практическое применение.
Эластичность — мера чувствительности одной переменной (например: спроса или предложения) к изменению другой (например: цены, дохода), показывающая, на сколько процентов изменится первый показатель при изменении второго на 1 %.
Внимание отдельных факторов в многофакторных моделях может быть охарактеризовано с помощью частных коэффициентов эластичности, которые в случае двухфакторной модели вычисляются по формулам:
Частные коэффициенты эластичности показывают, на сколько процентов измениться результирующий признак, если значение одного из факторных признаков измениться на 1%, а значение другого факторного признака останется не низменным.
В экономических исследованиях широкое применение находит такой показатель, как коэффициент эластичности. Если зависимость между переменными x и y имеет вид y=f(x) , то коэффициент эластичности Э вычисляется по формуле
Коэффициент эластичности Э показывает, на сколько процентов в среднем изменится результативный признак у при изменении фактора х на 1 % от своего номинального значения. Для линейной регрессии коэффициент эластичности равен
28. t-критерий Стьюдента. Алгоритм выполнения. Практическое применение.
t – критерий Стьюдента проводится с целью проверки значимости каждого параметра в отдельности.
Если проверяется значимость каждого параметра, то выбирают t – критерий Стьюдента и гипотеза строится 
… и все остальные параметры при факторе проверяются на = 0 по отдельности.
Алгоритм t – критерия:
1) Выдвигается H0 и H1 гипотезы, рассчитываются значения статистики, лежащей в основе критерия и дающей ему название – t-статистика.
Сконфигурировав линейнуб ф-ию (вызвав «линейн») и вызвав предварительно выбранный диапазон ячеек (2×5) статистику (в поле «статистика» = 1), стандартная ошибка соответствующего коэф-та находится под ним:
| b | A |
| СО (b) | СО (а) |
2) Из таблицы t-распределения с заданным уровнем значимости, кот задает № столбца и числом степеней свободы, рассчитанному на основе числа наблюдений № — кол-во оцениваемых параметров задает № строки, выбирается t-табличное.
| Число степеней свободы Уровни значимости | 1% | 5% | 10% |
| … | |||
| t 1% | t 5% |
N=10; Число степеней свободы = 8. Уровень значимости всегда берется по двустороннему критерию.
3) Сравниваем 
с каждым из табличных значений:
Следовательно, делается вывод о статистической значимости.
28. F-критерий Фишера. Алгоритм выполнения. Практическое применение.
F-критерий Фишера проводится с целью проверки значимости всей модели в целом.
Алгоритм F– критерия:
1) При выдвижении Н0 сравниваются (строятся отношения) дисперсий (Дфак – факторной и Дост – остаточной). И на основе их соотношения рассчитывается F-статистика:
F-статистика – величина, лежащая в основе критерия и дающая ему название.
Дисперсия рассчитывается в рамках дисперсионного анализа (см далее).
| B | A |
| СО (b) | СО (a) |
| R 2 | СО (y) |
| F-статистика | ЧСС |
 |
СО – стандартная ошибка
В нулевой гипотезе (Н0) делается предположение о равенстве дисперсии факторной и дисперсии остаточной.
H1 : Дф 
Дост
В случае, если удастся принять альтернативную гипотезу дополнительно делается сравнение дисперсии через неравенства: Дф 
Дост (делается дополнительно через дисперсионный анализ).
2) Из таблиц F-распределения выбираются критические (табличные) значения F -статистики. Таблица сформирована с учетом:
1. Уровня значимости (в заголовке таблицы);
2. Числа степеней свободы – ЧСС (равно номеру строки, номер строки в таблице F-критерий, t-критерий), для парной модели ЧСС = n -2 (n – число наблюдений);
3. Кол-во независимых переменных – НП (номер столбца).
| Кол-во НП ЧСС |
| = n-2 |
Число степеней свободы рассчитывается в общем виде по формуле:
ЧСС = n-k-1, k – кол-во независимых переменных
3) Выполняется сравнение F-статистики из п. 1 с F-критическими из п. 2 (2 при 1%, и 5%).
Для отклонения нулевой гипотезы требуется выполнение неравенства: 
В противном случае делается вывод о статистической значимости уравнения регрессии в целом.
Дисперсионный анализ
В дисперсионном анализе и в F-критерии Фишера рассматривают условно сконструированные дисперсии на основе соответствующих сумм квадратов. В основе лежит равенство (**) – разложение общей суммы квадратов отклонений СВ от среднего на факторную и остаточную сумму квадратов.
Для перехода к дисперсиям соответствующая сумма квадрата делится на ЧСС (свое для каждой суммы).
Определить ЧСС для расчета среднего значения СВ y, имеющей 5 значений.
| yi | Y1 | y2 | y3 | y4 | y5 |
 | |||||
 | -2 | -1 |
а — СО (а)* t табл 1%
Для линейной парной модели выполняется след связь между F и t критериями:
Таким образом, говорят о равносильности в данном частном случае этих двух критериев на практике.
В ряде прикладных программ и задач требуется оценить значимость коэффициента корреляции. Для этого строится гипотеза:
Н0: r генерал = 0
H1: r генерал не равно 0
Проверка осуществляется на основе расчета t – статистики через выборочный коэф-т корреляции, а затем на основе таблиц t – распределения выполняется сравнение рассчитанного значения с табличным.
Для линейной парной модели r 2 – это формула для расчета коэф-та детерминации: R 2 = r 2 .
Чем ближе R 2 к единице, тем лучше регрессия аппроксимирует эмпирические данные (приближает наблюдаемые данные).
Если R 2 = 1, то эмпирические точки лежат на линии регрессии, и между экзогенной и эндогенной переменными сущ-ет лин функциональная зависимость.
Если R 2 = 0, то изменение эндогенной переменной у всецело опр-ся изменением всех неучтенных в модели факторов (от изменения x не зависит).
| yi = |  | + |  |  |
 R 2 = 0,3 | 1 – R 2 = 0,7 |
В прикладных задачах всегда начинают исследование с линейной функции, затем берут либо степенную, либо показательную. Затем полином второй степени и в редком случае третьей.
http://helpiks.org/7-5944.html
http://lektsii.org/6-58481.html