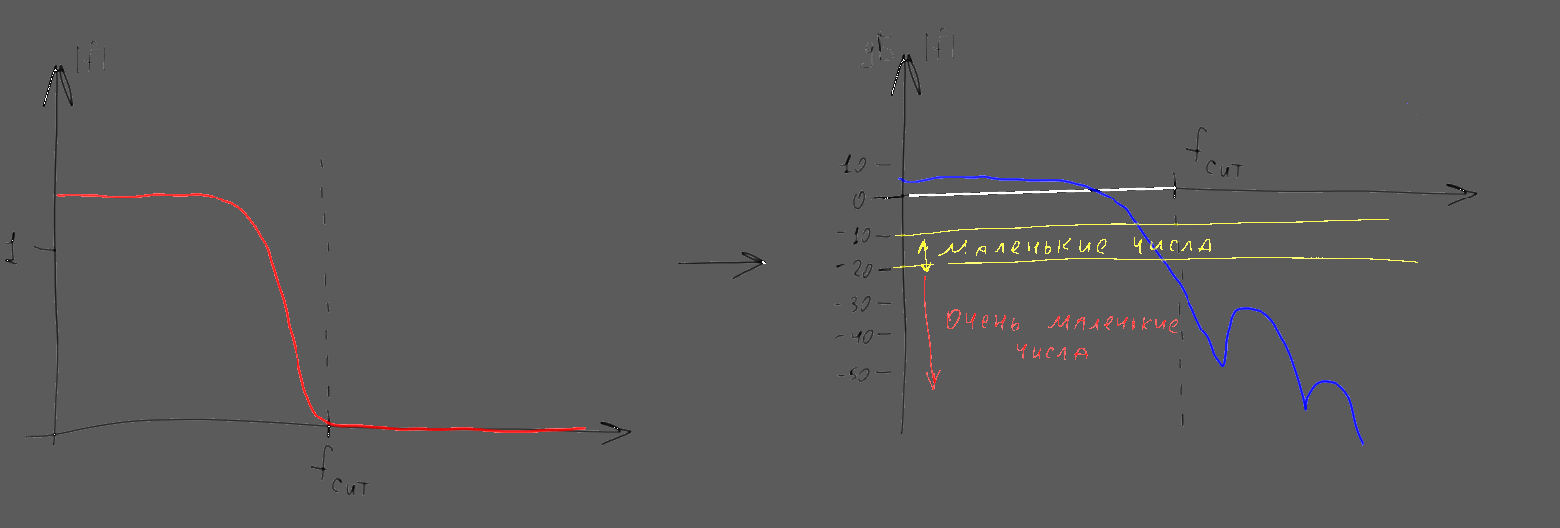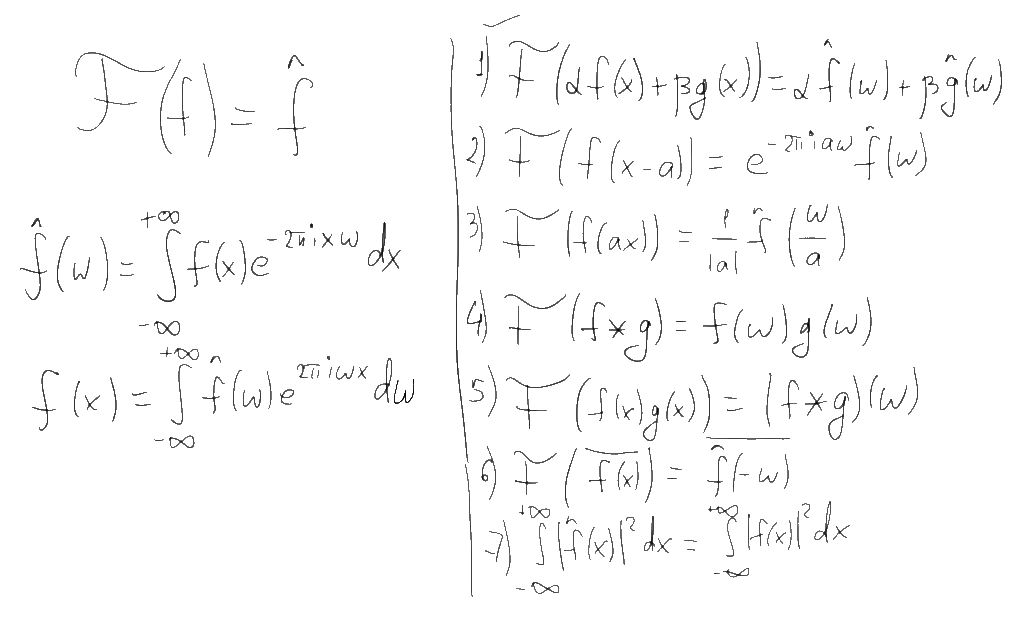Знак в уравнении фурье показывает

Закон Фурье – основной закон теплопроводности.

В 1807 году французский ученый Фурье доказал экспериментально, что во всякой точке тела (вещества) в процессе теплопроводности присуща однозначная взаимосвязь между тепловым потоком и градиентом температуры:

где Q – тепловой поток, выражается в Вт;

grad(T) – градиент температурного поля (совокупности числовых значений температуры в разнообразных местах системы в выбранный момент времени), единицы измерения К/м;

S – площадь поверхности теплообмена, м 2 ;

Градиент температуры получится характеризовать в виде векторной суммы составляющих по осям декартовых координат:

где i, j, k – ортогональные между собой единичные векторы, нацеленные по координатным осям.

Значит, данный закон устанавливает величину теплового потока при переносе тепла посредством теплопроводности.

Закон Фурье для поверхностной плотности теплового потока принимает вид:

Знак « минус» обозначает, что векторы теплового потока и градиента температуры разнонаправленные. Следует понимать, что теплота передается в направлении спада температуры.

И все же не лишним будет указать, что закон Фурье не принимает в расчет инерционность процесса теплопроводности, иначе говоря, в представленной модели колебание температуры в любой точке мгновенно распространяется на всё тело. Закон Фурье некорректно применять для характеристики высокочастотных процессов таких как, к примеру, распространение ультразвука, ударной волны.

Простыми словами о преобразовании Фурье

Я полагаю что все в общих чертах знают о существовании такого замечательного математического инструмента как преобразование Фурье. Однако в ВУЗах его почему-то преподают настолько плохо, что понимают как это преобразование работает и как им правильно следует пользоваться сравнительно немного людей. Между тем математика данного преобразования на удивление красива, проста и изящна. Я предлагаю всем желающим узнать немного больше о преобразовании Фурье и близкой ему теме того как аналоговые сигналы удается эффективно превращать для вычислительной обработки в цифровые.

(с) xkcd

Без использования сложных формул и матлаба я постараюсь ответить на следующие вопросы:

FT, DTF, DTFT — в чем отличия и как совершенно разные казалось бы формулы дают столь концептуально похожие результаты?
Как правильно интерпретировать результаты быстрого преобразования Фурье (FFT)
Что делать если дан сигнал из 179 сэмплов а БПФ требует на вход последовательность по длине равную степени двойки
Почему при попытке получить с помощью Фурье спектр синусоиды вместо ожидаемой одиночной “палки” на графике вылезает странная загогулина и что с этим можно сделать
Зачем перед АЦП и после ЦАП ставят аналоговые фильтры
Можно ли оцифровать АЦП сигнал с частотой выше половины частоты дискретизации (школьный ответ неверен, правильный ответ — можно)
Как по цифровой последовательности восстанавливают исходный сигнал

Я буду исходить из предположения что читатель понимает что такое интеграл, комплексное число (а так же его модуль и аргумент), свертка функций, плюс хотя бы “на пальцах” представляет себе что такое дельта-функция Дирака. Не знаете — не беда, прочитайте вышеприведенные ссылки. Под “произведением функций” в данном тексте я везде буду понимать “поточечное умножение”

Начать надо, наверное, с того что обычное преобразование Фурье — это некая такая штука которая, как можно догадаться из названия, преобразует одни функции в другие, то есть ставит в соответствие каждой функции действительного переменного x(t) её спектр или фурье-образ y(w):

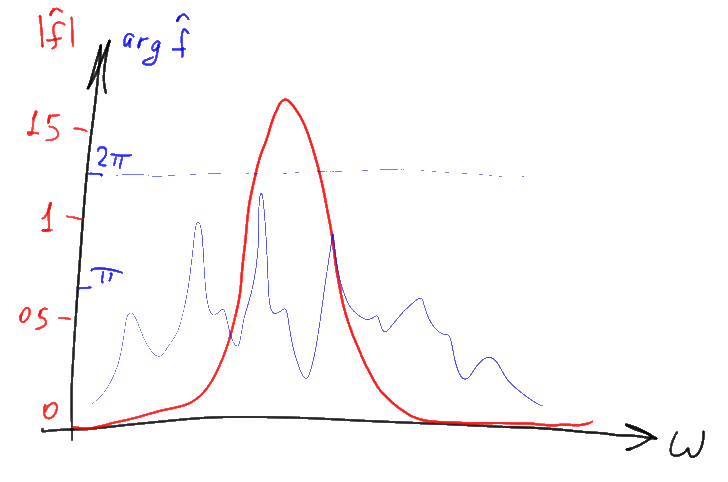
Если приводить аналогии, то примером аналогичного по смыслу преобразования может послужить например дифференцирование, превращающее функцию в её производную. То есть преобразование Фурье — такая же, по сути, операция как и взятие производной, и её часто обозначают схожим образом, рисуя треугольную “шапочку” над функцией. Только в отличие от дифференцирования которое можно определить и для действительных чисел, преобразование Фурье всегда “работает” с более общими комплексными числами. Из-за этого постоянно возникают проблемы с отображением результатов этого преобразования, поскольку комплексные числа определяются не одной, а двумя координатами на оперирующем действительными числами графике. Удобнее всего, как правило, оказывается представить комплексные числа в виде модуля и аргумента и нарисовать их по раздельности как два отдельных графика:

График аргумента комплексного значения часто называют в данном случае “фазовым спектром”, а график модуля — “амплитудным спектром”. Амплитудный спектр как правило представляет намного больший интерес, а потому “фазовую” часть спектра нередко пропускают. В этой статье мы тоже сосредоточимся на “амплитудных” вещах, но забывать про существование пропущенной фазовой части графика не следует. Кроме того, вместо обычного модуля комплексного значения часто рисуют его десятичный логарифм умноженный на 10. В результате получается логарифмический график, значения на котором отображаются в децибелах (дБ).

Обратите внимание что не очень сильно отрицательным числам логарифмического графика (-20 дБ и менее) при этом соответствуют практически нулевые числа на графике “обычном”. Поэтому длинные и широкие “хвосты” разнообразных спектров на таких графиках при отображении в “обычные” координаты как правило практически исчезают. Удобство подобного странного на первый взгляд представления возникает из того что фурье-образы различных функций часто необходимо перемножать между собой. При подобном поточечном умножении комплекснозначных фурье-образов их фазовые спектры складываются, а амплитудные — перемножаются. Первое выполняется легко, а второе — сравнительно сложно. Однако логарифмы амплитуды при перемножении амплитуд складываются, поэтому логарифмические графики амплитуды можно, как и графики фаз, просто поточечно складывать. Кроме того, в практических задачах часто удобнее оперировать не «амплитудой» сигнала, а его «мощностью» (квадратом амплитуды). На логарифмической шкале оба графика (и амплитуды и мощности) выглядят идентично и отличаются только коэффициентом — все значения на графике мощности ровно вдвое больше чем на шкале амплитуд. Соответственно для построения графика распределения мощности по частоте (в децибелах) можно не возводить ничего в квадрат, а посчитать десятичный логарифм и умножить его на 20.

Заскучали? Погодите, еще немного, с занудной частью статьи, объясняющей как интерпретировать графики, мы скоро покончим :). Но перед этим следует понять одну крайне важную вещь: хотя все вышеприведенные графики спектров были нарисованы для некоторых ограниченных диапазонов значений (в частности, положительных чисел), все эти графики на самом деле продолжаются в плюс и минус бесконечность. На графиках просто изображается некоторая “наиболее содержательная” часть графика, которая обычно зеркально отражается для отрицательных значений параметра и зачастую периодически повторяется с некоторым шагом, если рассматривать её в более крупном масштабе.

Определившись с тем, что же рисуется на графиках, давайте вернемся собственно к преобразованию Фурье и его свойствам. Существует несколько разных способов как определить это преобразование, отличающихся небольшими деталями (разными нормировками). Например в наших ВУЗах почему-то часто используют нормировку преобразования Фурье определяющую спектр в терминах угловой частоты (радианов в секунду). Я буду использовать более удобную западную формулировку, определяющую спектр в терминах обычной частоты (герцах). Прямое и обратное преобразование Фурье в этом случае определяются формулами слева, а некоторые свойства этого преобразования которые нам понадобятся — списком из семи пунктов справа:

Первое из этих свойств — линейность. Если мы берем какую-то линейную комбинацию функций, то преобразование Фурье этой комбинации будет такой же линейной комбинацией образов Фурье этих функций. Это свойство позволяет сводить сложные функции и их фурье-образы к более простым. Например, фурье-образ синусоидальной функции с частотой f и амплитудой a является комбинацией из двух дельта-функций расположенных в точках f и -f и с коэффициентом a/2:

Если взять функцию, состоящую из суммы множества синусоид с разными частотами, то согласно свойству линейности, фурье-образ этой функции будет состоять из соответствующего набора дельта-функций. Это позволяет дать наивную, но наглядную интерпретацию спектра по принципу “если в спектре функции частоте f соответствует амплитуда a, то исходную функцию можно представить как сумму синусоид, одной из которых будет синусоида с частотой f и амплитудой 2a”. Строго говоря, эта интерпретация неверна, поскольку дельта-функция и точка на графике — это совершенно разные вещи, но как мы увидим дальше, для дискретных преобразований Фурье она будет не так уж и далека от истины.

Второе свойство преобразования Фурье — это независимость амплитудного спектра от сдвига сигнала по времени. Если мы подвинем функцию влево или вправо по оси x, то поменяется лишь её фазовый спектр.

Третье свойство — растяжение (сжатие) исходной функции по оси времени (x) пропорционально сжимает (растягивает) её фурье-образ по шкале частот (w). В частности, спектр сигнала конечной длительности всегда бесконечно широк и наоборот, спектр конечной ширины всегда соответствует сигналу неограниченной длительности.

Четвертое и пятое свойства самые, пожалуй, полезные из всех. Они позволяют свести свертку функций к поточечному перемножению их фурье-образов и наоборот — поточечное перемножение функций к свертке их фурье-образов. Чуть дальше я покажу насколько это удобно.

Шестое свойство говорит о симметрии фурье-образов. В частности, из этого свойства следует что в фурье-образе действительнозначной функции (т.е. любого “реального” сигнала) амплитудный спектр всегда является четной функцией, а фазовый спектр (если его привести к диапазону -pi. pi) — нечетной. Именно по этой причине на графиках спектров практически никогда не рисуют отрицательную часть спектра — для действительнозначных сигналов она не дает никакой новой информации (но, повторюсь, и нулевой при этом не является).

Наконец последнее, седьмое свойство, говорит о том, что преобразование Фурье сохраняет “энергию” сигнала. Оно осмысленно только для сигналов конечной продолжительности, энергия которых конечна, и говорит о том, что спектр подобных сигналов на бесконечности быстро приближается к нулю. Именно в силу этого свойства на графиках спектров как правило изображают только “основную” часть сигнала, несущую в себе львиную долю энергии — остальная часть графика просто стремится к нулю (но, опять же, нулем не является).

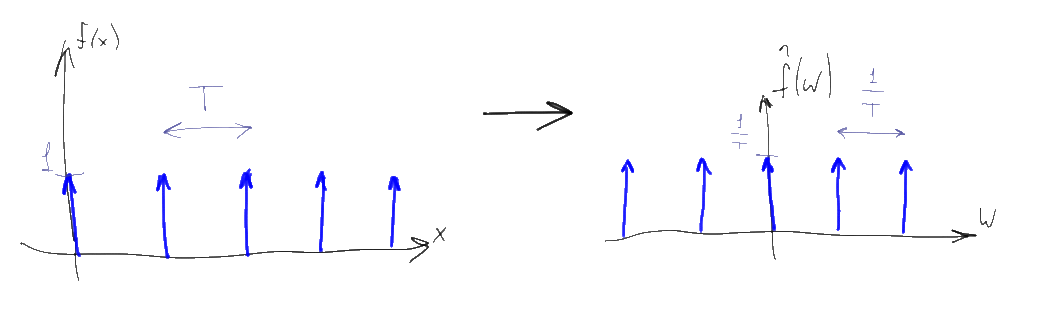
Вооружившись этими 7 свойствами, давайте посмотрим на математику “оцифровки” сигнала, позволяющую перевести непрерывный сигнал в последовательность цифр. Для этого нам понадобится взять функцию, известную как “гребенка Дирака”:

Гребенка Дирака — это просто периодическая последовательность дельта-функций с единичным коэффициентом, начинающаяся в нуле и идущая с шагом T. Для оцифровки сигналов, T выбирают по возможности малым числом, T

Закон Фурье | Все это важно с 6 часто задаваемыми вопросами

Content

Закон теплопроводности Фурье

Закон Фурье теплопроводности может иметь следующий вид:

«Скорость теплопередачи от материала или образца прямо пропорциональна площади поперечного сечения (перпендикулярной площади), через которую проходит тепло, и разности температур вдоль торцевых поверхностей материала».

Мы можем записать это утверждение математически как,

q = скорость теплопередачи в ваттах (Вт или Дж / с)

K = теплопроводность материала или образца (Вт / м · K)

A = Площадь поперечного сечения, через которую проходит тепло, в м 2

dT = разница температур между горячей и холодной сторонами в K (Кельвинах)

dx = Толщина материала в м (толщина между горячей и холодной стороной)

Самое важное: здесь в уравнении отрицательный знак означает, что тепло всегда течет в направлении уменьшения температуры.

Уравнение закона Фурье

Уравнение закона теплопроводности получено выше. Он широко используется для решения задач теплопроводности и анализа. Суть уравнения остается прежней, но параметры меняются в зависимости от формы и положения объекта.

Сферические координаты закона Фурье

Закон теплопроводности, примененный к цилиндру и уравнению, приведен ниже:

Здесь, в любом месте

r — радиус рассматриваемого цилиндрического участка,

Цилиндрические координаты закона Фурье

Закон теплопроводности, применяемый к цилиндру и уравнению, приведен ниже:

в любом месте площадь A = 2πrL,

r — радиус рассматриваемого цилиндрического участка,

Эксперимент с законом Фурье

Обычно у металлов есть свободная подвижность электронов внутри объекта. Это причина его хорошей проводимости.

Рассмотрим двухблочный A и B,

Блок А очень горячий

Блок Б холодный

Предположим, мы соединяем эти два блока и изолируем все остальные внешние поверхности. Изоляция предназначена для уменьшения потерь тепла от блока. Вы можете быстро понять, что тепловая энергия будет перетекать от горячего блока к холодному. Передача тепла будет продолжаться до тех пор, пока оба блока не достигнут одинаковой температуры (температурного равновесия).

Это один из способов передачи тепла в обоих блоках. Это кондуктивный режим теплопередачи. Используя уравнение закона теплопроводности, мы можем рассчитать теплопередачу с помощью этого эксперимента. Выполнение в лаборатории теплопередачи (машиностроение и химическая инженерия) очень информативно и важно с практической точки зрения.

История закона Фурье

Фурье начал свою работу по выражению теплопроводности в 1822 году. Он также дал понятие ряда Фурье и интеграла Фурье. Он был математиком. Его закон теплопроводности хорошо известен благодаря его имени «закон теплопроводности Фурье».

Единицы закона Фурье

Для теплопередачи сформулирован закон Фурье теплопроводности. Итак, мы можем рассматривать для него единицу теплоотдачи. Единицей теплоотдачи является ватт (Дж / с) Вт.

Допущения закона Фурье

Есть некоторые предположения о законе теплопроводности Фурье. Закон применяется только при соблюдении и соблюдении следующих условий.

Кондуктивная теплопередача будет происходить в стационарных условиях объекта.
Поток тепла должен быть однонаправленным.
Температурный градиент должен быть постоянным на протяжении всего процесса, а температурный профиль должен быть линейным.
Внутреннее тепловыделение должно быть нулевым.
Ограничивающие поверхности должны быть должным образом изолированы.
Материал должен быть однородным и изотропным.

Пример закона теплопроводности Фурье

Есть много примеров закона теплопроводности в повседневной жизни. Некоторые примеры обсуждаются ниже.

В кружке горячий кофе. Теперь вы знаете, что тепло будет передаваться с горячей стороны на холодную. Здесь передача тепла происходит от внутренней стенки к внешней стенке кружки. Это кондуктивный перенос тепла, основанный на законе теплопроводности Фурье.

В качестве примера можно рассмотреть стену нашего дома.

Если в стержне происходит внутреннее тепловыделение, тепло будет течь во внутренней части к внешним поверхностям.

Можно потрогать любое электрическое и электронное оборудование. Вы получите немного тепла. Все эти устройства могут быть примером закона Фурье.

Число Фурье

Это безразмерное число, полученное с помощью безразмерного уравнения теплопроводности..

Число Фурье обозначается F_o

L — длина пластины (диаметр в случае цилиндра) в м.

K — коэффициент градиентного переноса

Поток закона Фурье

Согласно информации закон теплопроводности,

Тепловой поток можно определить как тепловой поток на единицу площади в единицу времени прямо пропорционален разнице температур между горячей и холодной стороной (температурный градиент).

Тепловой поток

Уравнение теплового потока

Уравнение теплового потока приведено ниже.,

q- тепловой поток в Вт / м 2

K — теплопроводность, Вт / м · K

ΔT / ΔX — температурный градиент,

Агрегаты теплового потока

Единица теплового потока — Вт / м 2

Часто задаваемые вопросы

Что такое закон Фурье

«Скорость теплопередачи через материал или образец прямо пропорциональна площади поперечного сечения, через которую проходит тепло, и разности температур вдоль торцевых поверхностей материала».

Мы можем записать это утверждение математически как,

q = скорость теплопередачи в ваттах (Вт или Дж / с)

K = теплопроводность материала или образца (Вт / м · K)

A = Площадь поперечного сечения, через которую проходит тепло, в м 2

dT = разница температур между горячей и холодной сторонами в K (Кельвинах)

dx = Толщина материала в м (толщина между горячей и холодной стороной)

Каковы предположения закона теплопроводности Фурье?

Есть некоторые предположения о законе теплопроводности Фурье. Закон применяется только при соблюдении и соблюдении следующих условий. Закон теплопроводности Фурье можно сравнить с законом охлаждения Ньютона и законом диффузии Фика. Допущения в каждом законе разные.

Кондуктивная теплопередача будет происходить в стационарных условиях объекта.
Поток тепла должен быть однонаправленным.

Температурный градиент не изменится, а температурный профиль должен быть линейным.
Внутреннее тепловыделение должно быть нулевым.
Ограничивающие поверхности должны быть должным образом изолированы.
Материал должен быть однородным и изотропным.

Что является доказательством закона теплопроводности Фурье и отрицательного градиента?

Доказательство закона теплопроводности Фурье уже дано в теме «Закон Фурье».

Отрицательный градиент используется, потому что тепло всегда течет при понижении температуры.

Этот вопрос очень важен для собеседования, потому что интервьюер всегда старается проверить ваши фундаментальные знания.

Чем закон теплопроводности Фурье противоречит теории относительности?

Закон Фурье противоречит теории относительности из-за его мгновенного распространения тепла через диффузию тепла. Если мы рассмотрим зависящую от времени диффузию тепла с помощью уравнения в частных производных, то рост теплового потока будет со временем релаксации. На этот раз порядка 10 -11 . Распространение тепла в природе занимает бесконечное время. Время релаксации незначительно.

Если исключить время релаксации, уравнение станет законом теплопроводности Фурье. Это нарушает популярную теорию Эйнштейна (теория относительности). Скорость света в вакууме составляет 2.998 * 10. 8

Чем физика, лежащая в основе закона Фурье, отличается от физики, лежащей в основе закона охлаждения Ньютона

Как мы уже знаем, закон Фурье используется для теплопроводности, а закон охлаждения Ньютона — для конвективной теплопередачи. Предположим, у вас есть вопрос, почему для анализа скорости теплопередачи требуются два разных закона. Причина в том, что режимы теплопередачи отличаются от индивидуальной физики.

Перенос тепла проводимостью происходит за счет микроскопической диффузии и столкновений молекул или квазичастиц внутри объекта из-за разницы температур. Если мы видим микроскопически, то диффузный и сталкивающийся любой материал включает в себя молекулы, электроны, атомы. Они передают друг другу кинетическую и потенциальную энергию микроскопически. Эта энергия известна как внутренняя энергия объекта. Закон гласит, что теплопроводность является законом Фурье.

Конвекционную теплопередачу в любом объекте можно определить как теплопередачу от одной молекулы к другой за счет перемещения жидкостей или потока жидкости. Закон охлаждения Ньютона определяет конвекционную теплопередачу.

Физика, используемая для отдельного процесса, различна. Следовательно, регулирующий закон для человека отличается.

В чем сходство между законом вязкости Ньютона, законом теплопроводности Фурье и законом диффузии Фика?

Это аналогия между этими уравнениями.

Закон Фурье теплопроводности

В нем описан процесс теплопроводности. Уравнение можно записать следующим образом:

Уравнение теплового потока приведено ниже.,

q- тепловой поток в Вт / м 2

K — теплопроводность, Вт / м · K

ΔT / ΔX — температурный градиент,

Закон диффузии Фика

Он используется для описания и определения процесса массопереноса. Уравнение массопереноса можно записать следующим образом:

(dC / dx) — градиент концентрации

D — коэффициент диффузии транспортных свойств

Закон вязкости Ньютона

Он используется для передачи импульса и широко используется для изучения вязкости любой жидкости.

Здесь (du / dx) — градиент скорости

μ — вязкость жидкости

Таким образом, вы можете сразу проанализировать три разных закона относительности этих уравнений.

Чтобы прочитать больше статей по соответствующей теме, пожалуйста нажмите сюда

Последнее сообщение о машиностроении

источники:

http://habr.com/ru/post/196374/

http://ru.lambdageeks.com/fouriers-law-its-all-important/