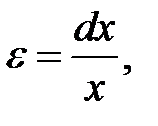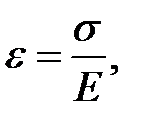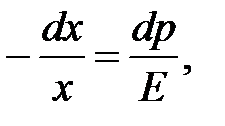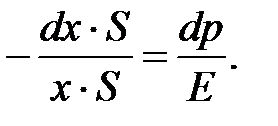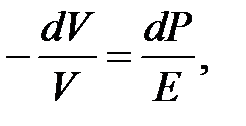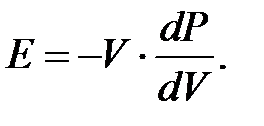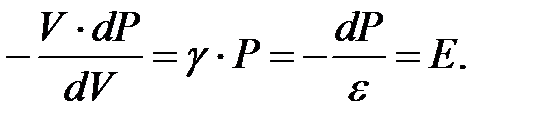Звуковая волна с точки зрения термодинамики уравнение

Термодинамика звука в газе

ИЗУЧЕНИЕ ЗАВИСИМОСТИ СКОРОСТИ ЗВУКА В ВОЗДУХЕ

ОТ ТЕМПЕРАТУРЫ

Термодинамика звука в газе

Звуковая волна в газе представляет собой продольную волну в упру­гой среде, в которой происходят периодические сжатия и разрежения газа, например воздуха. Как известно из механики, скорость распространения упругих колебаний определяется выражением:

,

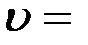
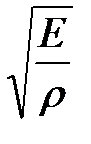
гдеЕ – модуль упругости среды, ρ– плотность среды.

Воспользуемся уравнениями термодинамики для нахождения скорости звука в газе. Выде­лим мысленно в газе прямоугольный парал­лелепипед, площадь основания которого S, a высота – x, параллельная вектору скорости рас­пространения волны.

Этот параллелепи­пед будет испытывать продольную деформацию dx, причём относительная деформация согласно закону Гука:

где s – сила давления, испытываемая едини­цей поверхности выбранного объёма.

В дан­ном случае:

где dp– давление, избыточное над равновесным.

Умножим и разделим левую часть на S:

Последнее выражение можно представить в виде:

где dV и V –- изменение объема и объём параллелепипеда. Отсюда:

Так как звуковые колебания имеют довольно высокую частоту (сотни и ты­сячи герц), а теплопроводность газа относительно мала, то смены сжатия и разрежения в газе происходят настолько быстро, что процесс можно считать адиабатным (PV g = const, g – коэффициент Пуассона). Отсюда получаем:

PgV g -1 dV + V g dP = 0 ,

Умножая и деля последнее выражение на молярный объём V_m и ис-пользуя уравнение Менделеева – Клапейрона, получаем окончательное выра­жение для зависимости скорости звука в газе от температуры:

(2)

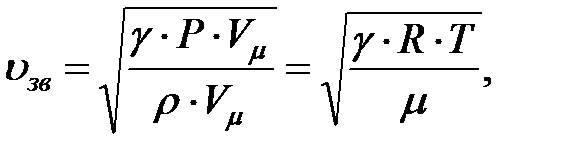
где m – молярная масса газа, R – универсальная газовая постоянная, Т – абсолют­ная температура газа.

Подставляя в последнюю формулу значения величин для воздуха и заменяя абсолютную температуру температурой t по шкале Цельсия, получим удобное для практического применения соотношение:

Дата добавления: 2016-03-15 ; просмотров: 1419 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Зависимость скорости звука от термодинамических условий. Термодинамические формы уравнения Бернулли

Зависимость скорости звука от термодинамических условий. Термодинамические формы уравнения Бернулли

Зависимость скорости звука от термодинамических условий. Термодинамические формы уравнения Бернулли. Используя описанную выше термодинамическую зависимость, мы анализируем характеристики газового потока. Скорость звука в Газе по зависимости (15.13) может быть рассчитана при двух различных допущениях. 276. 1) процесс распространения возмущений изотермический (T-sOP).Затем, согласно уравнениям Клапейрона 2)процесс распространения возмущения является адиабатическим. Далее следует формула Пуассона(15.24). В то же время Рк Формула (15.27) была получена Ньютоном, Лапласом (15.2 B).

Интересно отметить, что значение скорости звука в газе имеет тот же порядок, что и значение среднего свободного пробега газа. Людмила Фирмаль

• На основании проведенного эксперимента было установлено, что экспериментальное значение скорости звука хорошо совпадает с формулой (15.28), поэтому было установлено, что процесс распространения возмущений газа близок к термоизоляции. Заметим, что разница в величине а, определяемая по формулам (15.27) и (15.2 в), не превышает 20%. Рассчитайте скорость звука в воздухе при температуре 20°C molecule.

• Известно из кинетической теории газов среднеквадратичное значение. Эта скорость V ^ = l / ZKT, следовательно^ 0.68 UM. Во-первых, мы используем уравнение KLA Пейрона Менделеева для представления внутренней энергии E с давлением P. Подставляя это выражение в(15.29), получим Подставляя уравнение (15.29) вместо 1 (15.22), вы получаете другую форму уравнения Бернулли.

Как уже было сказано, низкая теплоемкость и теплопроводность газов обеспечивают условия для процесса, близкого к теплоизоляции, поэтому в дальнейшем вы получите все результаты для условий процесса теплоизоляции. Людмила Фирмаль

• Вы можете записать другую форму уравнения Бернулли, заменив QCT на a2 (на 15.31) (на 15.28). Обратите внимание, что в точке (15.33) скорость звука равна local. It относится к той же площади поперечного сечения, что и скорость. Представленная форма уравнения Бернулли, включающая термодинамические свойства, заполнена не только коротким отрезком линии потока, что позволяет пренебречь боковой диффузией тепловой и механической энергии, но и изолированным потоком полного газа.

Смотрите также:

Возможно эти страницы вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Общая физика. Механика. Молекулярная физика, Лабораторный практикум (стр. 6 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7

. (3)

Переход от состояния 1 к состоянию 2 происходит адиабатически, поэтому параметры их связаны уравнением Пуассона (2), которое примет вид

(4)

Преобразуем уравнение (3). Возведем обе его части в степень g:

.

Разделим почленно полученное равенство на выражение (4),

.

Прологарифмируем последнее равенство:

,

Так как величины h1 и h2, выраженные в миллиметрах ртутного столба, очень малы по сравнению с Н и, следовательно, дроби h1/H и (h1 – h2)/(H + h2) также незначительны, для нахождения логарифма можно воспользоваться выражением

,

где х – малая величина. Поскольку х2 и, тем более, х3 – величины высших порядков малости, ими можно пренебречь, то lg(1 + x) @ x и, следовательно,

Пренебрегая величиной h2 в сумме H + h2, получим расчетную формулу

. (5)

1. Открыв кран K, накачать насосом воздух в баллон В и закрыть кран.

2. Измерить разность уровней h1, когда разность уровней жидкости в манометре стабилизируется (т. е. температура воздуха в баллоне станет равной комнатной температуре).

3. Открыть кран K, и когда избыток воздуха выйдет из баллона (прекратится характерное шипение воздуха), быстро закрыть его.

4. Измерить разность уровней h2, когда разность уровней жидкости в манометре стабилизируется.

5. Повторить 10 раз пп.1-4 и оформить результаты измерений в виде таблицы:

Здесь Dh1 и Dh2 – приборная ошибка в измерении h1 и h2, Dh1 = Dh2 = 1 мм.

6. Вычислить g для каждого измерения по формуле (5); найти среднее значение .

7. Рассчитать погрешность измерения. В этом случае (величина g определяется многократно) допускается рассчитать его как среднее квадратическое для серии n измерений:

.

8. Привести окончательный результат в виде .

1. Что такое теплоемкость, молярная теплоемкость, удельная теплоемкость? Как связаны эти параметры? Какова размерность теплоемкости? От чего зависит молярная теплоемкость?

2. Почему Cp > CV с точки зрения первого начала термодинамики?

3. Какой процесс называют адиабатическим? Каким уравнением описывается адиабатический процесс?

4. Какие термодинамические процессы рассматриваются в данной работе? Изобразите эти процессы в координатах р – V.

5. Почему измерение давления следует производить не сразу после выпуска воздуха, а через некоторое время?

6. Для чего баллон покрыт теплоизолирующей оболочкой?

Работа 11. определение отношения

теплоемкости воздуха при постоянном давлении к теплоемкости при постоянном объеме

методом стоячей волны

Цель работы – определить g = Cp/CV методом стоячей звуковой волны.

Звуковые волны являются продольными волнами сжатия и расширения, следовательно, их скорость зависит от упругих свойств среды. Из теории следует, что скорость звуковых волн в твердых телах

где ρ – плотность среды; Е – модуль Юнга.

Для газов и жидкостей скорость звука

(1)

где K – модуль объемной упругости.

Газы обладают способностью сопротивляться изменению его объема, т. е. газам присуща объемная упругость, проявляющаяся в изменении давления газа р при изменении его объема V. По закону Гука для объемной деформации, изменение давления газа dp при малом изменении его объема dV прямо пропорционально относительной объемной деформации:

(2)

Для газа значение K зависит от вида термодинамического процесса.

При распространении волн в газе вследствие сжатий и расширений происходит изменение температуры различных участков среды. Для волн высокой частоты, например звуковых, температуры отдельных участков не будут успевать выравниваться за время одного колебания. Поэтому кратковременные процессы сжатия и расширения можно считать происходящими без теплообмена, т. е. адиабатическими. Уравнение Пуассона для адиабатического процесса

(3)

где – отношение теплоемкостей при постоянном давлении и постоянном объеме.

Дифференцируя уравнение (3), получим

(4)

Из формул (2) и (4) получим

(5)

Согласно уравнению Менделеева – Клапейрона

(6)

где μ – молярная масса; Т – абсолютная температура; R – универсальная газовая постоянная.

Подставляя формулы (5), (6) в (1), запишем

(7)

Таким образом, определение γ сводится к измерению скорости звука и абсолютной температуры воздуха. В данной работе скорость звука определяется методом стоячих волн – методом Кундта.

Если в трубе, один конец которой закрыт, возбудить звуковые колебания, в ней в результате наложения двух встречных волн (прямой и отраженной) с одинаковыми частотами и амплитудами будут возникать стоячие волны. В определенных точках амплитуда стоячей волны равна сумме амплитуд обоих колебаний и имеет максимальное значение; такие точки называются пучностями. В других точках результирующая амплитуда равна нулю, такие точки называются узлами. Расстояние между cоседними пучностями равно l/2, где l – длина бегущей звуковой волны. Таким образом, измерив расстояние (l/2) между двумя ближайшими пучностями, можно найти длину бегущей звуковой волны l. Фазовая скорость волны

где n – частота колебаний.

В экспериментальную установку (см. рисунок) входят: стеклянная труба, в которой создается стоячая волна, звуковой генератор (ЗГ), микровольтметр, частотомер (Ч). В стеклянную трубу вмонтированы неподвижный микрофон (М) и телефон (Т), который может свободно перемещаться вдоль оси трубы.

Звуковой генератор вырабатывает синусоидальное напряжение звуковой частоты, которое подается на телефон. Переменный ток приводит в колебательное движение мембрану телефона, являющуюся излучателем звуковой волны. Отраженная от противоположной стенки трубы волна движется навстречу излучаемой и происходит их наложение. В результате в трубе возникает стоячая звуковая волна. В микрофоне происходит преобразование механической энергии волны в энергию электрического тока, величина которого измеряется микровольтметром. Частота звуковой волны устанавливается на генераторе, точное значение частоты измеряется частотомером. При перемещении телефона вдоль трубы ток в цепи микрофона будет меняться от минимального, когда микрофон попадает в узел, до максимального, когда он попадает в пучность. Таким образом, следя за показаниями микровольтметра, можно найти положения нескольких пучностей стоячей волны и вычислить ее длину.

Порядок выполнения работы

1. Включить нажатием тумблеров «ВКЛ» и «СЕТЬ» звуковой генератор, частотомер и вольтметр, прогреть приборы в течение 3-5 мин.

2. После прогрева установить необходимую частоту колебаний на звуковом генераторе (удобен диапазон Гц), измеряя точное значение частоты частотомером.

3. Перемещая телефон вдоль трубы, найти ближайшее к левому концу трубы положение телефона lk, при котором показание микровольтметра максимально, записать его в таблицу.

4. Зафиксировать еще несколько положений, при которых показания микровольтметра максимальны.

5. Вычислить разность между соседними отсчетами dlk = = lk – lk-1 для всех наблюдавшихся пучностей, усреднить полученные значения.

6. По среднему расстоянию между пучностями рассчитать длину бегущей волны l = и скорость по формуле (8).

7. Повторить пп.3-6 для четырех-пяти значений частоты в интервале Гц.

8. Измерить температуру воздуха в помещении.

9. Рассчитать g по формуле (7) при m = 2,9×10-2 кг/моль (воздух) и R = 8,31 Дж/(моль×К).

10. Результаты измерений и расчетов записать в таблицу: